Dat de gele oppervlakte 1 is is direct te zien;'t is een vierkant van 1 bij 1. We gaan nu proberen te laten zien dat alle oppervlaktes aan elkaar gelijk zijn; dan zijn ze meteen allemaal gelijk aan de eerste, dus aan 1.
Hoe is dat te zien?

Eerst maar eens terug naar de rij s_n:     s_n = ³/₂ • ⁵/₄ • ... • ^{(2n - 1)}/_{(2n - 2)}
Maar dan geldt:

En dus: 

En dat gebruiken we weer bij a_{n + 1}:

We bewijzen nu eerst het volgende verband (vraag niet waar we het vandaan halen):

(1)

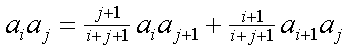
Dat bewijzen we door gewoon de formule erboven voor a_{n + 1} in te vullen:

Wat hebben we aan dit verband?
Stel dat we een verzameling rechthoeken van dezelfde kleur hebben. Die ziet er zo uit:

a₀a_n-1 + a₁a_n-2 + ... +  a_n-2a₁ + a_n-1a₀

Het verband (1) levert dan :

Als je gelijk termen samenneemt (1^e,  2^e + 3^e,  4^e + 5^e, ...)  zie je dat alle coëfficiënten 1 worden.
Conclusie:  a₀a_n-1 + a₁a_n-2 + ... +  a_n-2a₁ + a_n-1a₀  =  a₀a_n + a₁a_n-1 + ... +  a_n-1a₁ + a_na₀
Dus als we beginnen met a₀a₀ krijgen we achtereenvolgens:

Het zijn inderdaad precies de gekleurde series rechthoeken in bovenstaande figuur, en die zijn dus inderdaad allemaal 1.