De formule van Wallis zegt:  W = 2/1 • 2/3 • 4/3 • 4/5 • 6/5 • 6/7 • ..... = p/2
De tabel hiernaast laat zien hoe groot het product is na een aantal factoren.
De getallen bij een oneven aantal factoren uit deze tabel vormen een dalende reeks, de even nummers een stijgende reeks.
Laten we deze beide rijen apart bekijken, en proberen ze met elkaar te vergelijken.
Eerst de oneven serie, te beginnen bij n = 1:
n rij herschreven
1 2/1 2
2 2/1 • 2/3 • 4/3 4 • (2•2/3•3)
3 2/1 • 2/3 • 4/3 • 4/5 • 6/5 6 • (2•2•4•4)/(3•3•5•5)
4 2/1 • 2/3 • 4/3 • 4/5 • 6/5 • 6/7 • 8/7 8 • (2•2•4•4•6•6)/(3•3•5•5•7•7)
5 2/1 • 2/3 • 4/3 • 4/5 • 6/5 • 6/7 • 8/7 • 8/9 • 10/9 10 •  (2•2•4•4•6•6•8•8)/(3•3•5•5•7•7•9•9)
enz....
aantal factoren product
1 2
2 1,33
3 1,78
4 1,42
5 1,71
6 1,46
7 1,67
8 1,49
9 1,65
10 1,50
De rechterkolom laat duidelijk steeds dezelfde soort breuken zien, voorafgegaan door een factor 2n.
Daarom definiλren we nu eerst:
Dan kun je de oneven rijen hierboven schrijven als


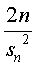
Nu gaan we proberen (met deze sn  in ons achterhoofd) ook de even rijen te ordenen, te beginnen bij n = 2:
n rij "trucje" herschreven
2 2/1 • 2/3 2/1 • 2/3 • 1/3 • 3 3 • (2•2)/(3•3)
3 2/1 • 2/3 • 4/3 • 4/5 2/1 • 2/3 • 4/3 • 4/5 • 1/5 • 5 5 • (2•2•4•4)/(3•3•5•5)
4 2/1 • 2/3 • 4/3 • 4/5 • 6/5 • 6/7 2/1 • 2/3 • 4/3 • 4/5 • 6/5 • 6/7 • 1/7• 7 7 • (2•2•4•4•6•6)/(3•3•5•5•7•7)
5 enz....
Met dit "trucje"kun je de even rij schrijven als
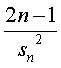
De werkelijke waarde van de rij van Wallis zit tussen deze twee in:
Daaruit volgt trouwens:

(deze ONGELIJKHEID 1 zullen we verderop gebruiken)

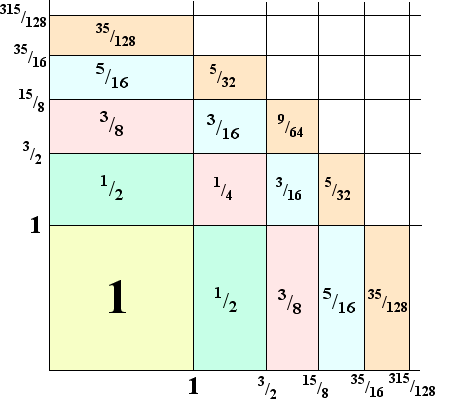Wat we er allemaal aan hebben zien we in de figuur hiernaast.
Daar zijn op de x-as en de y-as de opeenvolgende waarden van sn gezet. Kijk naar de rechthoeken met een zelfde kleur. Die vormen langzaam een soort van kwartcirkel. Kijk eens aan: "Now we're getting somewhere!" We willen immers uiteindelijk toch uitkomen bij p, nietwaar?
Als we de oppervlaktes van  rechthoeken van dezelfde kleur bij elkaar optellen vonden we iets wonderbaarlijks:
Er komt steeds 1 uit!!!!!!!!!


Het bewijs dat dat inderdaad zo is is nogal lastig (en trouwens ook nogal saai; het wemelt van de indices i, j  en de sommaties). Voor de echte doorbijters staat het HIER, maar ik ga intussen verder met het feit dat de rechthoeken van dezelfde kleur samen oppervlakte 1 hebben.
Dat betekent dat, als we n kleuren rechthoeken nemen, de totale gekleurde oppervlakte gelijk is aan n (de gekleurde oppervlakte hiernaast is dus 5).
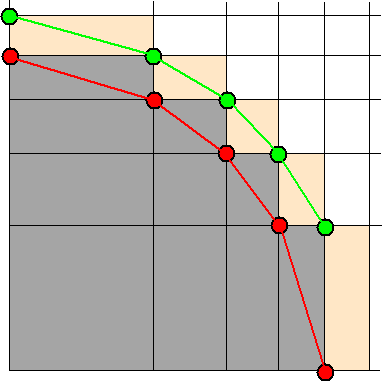
Kijk naar de tweede figuur hiernaast. We bekijken de oppervlakte van het grijze gebied. Dat zijn de eerste 4 series rechthoeken (n = 4) en de oppervlakte daarvan zal dus 4 zijn..
De rode punten zijn de hoekpunten linksonder van de laatste serie rechthoeken, de groene punten zijn de hoekpunten linksboven.
De hoekpunten linksonder zijn de punten (s0, s4)(s1, s3)(s2, s2)(s3, s1)(s0, s4). In het algemene geval  (si, sj) met   i + j = n
Voor de afstand  (r) van zo'n punt tot de oorsprong geldt (met behulp van ongelijkheid (1) hierboven):

 

 
 
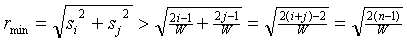Daarmee hebben we een ondergrens voor de afstand van de rode punten tot de oorsprong gevonden.

De hoekpunten rechtsboven zijn de punten  (s0,s5),(s1,s4)(s2,s3)(s3,s2)(s4,s1).
In het algemene geval  (si, sj) met i + j = n + 1, en op dezelfde manier vinden we:
 
 
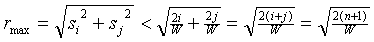Nou komt het: de gehele grijze oppervlakte ligt  dus tussen een kwartcirkel met straal  rmin  en een kwartcirkel met straal rmax.
Maar die oppervlakte is n; dus moet gelden:  1/4prmin2 < n < 1/4prmax2

Met de rmin en rmax van hierboven geeft dat:

Omschrijven  levert dan eindelijk het resultaat waarnaar we zo wanhopig op zoek waren:

Omdat dit voor elke n geldt kunnen we (n - 1)/n en (n + 1)/n zo dicht als we maar willen bij 1 krijgen, dus zal W gelijk zijn aan p/2