| Jazeker! Dat kan! |
|
|
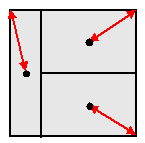
Eerst moet je je realiseren dat het gaat om de
hoeken, want die zijn het "verst weg". Nou zijn er
helaas 4 hoeken en maar 3 agenten. Dus zal ťťn agent twee
hoeken voor zijn rekening moeten nemen. De opstelling zal er
daarom ongeveer moeten uitzien als hiernaast. De rode lijnen
geven de afstand tot de hoeken aan.
Als de agenten precies op het snijpunt van de diagonalen van een
rechtshoek staan zijn alle punten op alle zijden van het plein
te bereiken. |
|
| En de efficiŽntste manier wordt
bereikt als die drie rechthoeken precies aansluiten. Immers als
twee rechthoeken zouden overlappen zouden we ze beiden ietsje
kleiner kunnen maken. Dan zou het hele plein nog steeds
bestreken worden, maar dan zouden de afstanden van de agenten
tot hun verste punt kleiner zijn geworden. Dat zou een betere
manier zijn. |
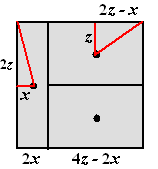
Noem de zijde van het plein 4z
en stel dat de linker rechthoek breedte 2x heeft. Dan
gelden de afmetingen zoals hiernaast.
De beste indeling krijgen we als de afstanden tot de hoeken voor
alle agenten gelijk zijn (als dat niet zo is kan het weer
efficiŽnter door de rechthoek van de ene agent ietsje kleiner
te maken en die van de anderen ietsje groter).
Pythagoras:
(2z)2 + x2 = z2
+ (2z - x)2 ř
4z2 + x2 = z2
+ 4z2 - 4zx + x2
Daaruit volgt eenvoudig x = 0 of x =
1/4z
Ofwel: bij een plein van 80 bij 80 is de ene rechthoek
10 bij 80 en zijn de andere twee 70 bij 40. |
|
De afstand voor de ene agent is
dan ÷(52 + 402)
= ÷1625
De afstand voor beide andere agenten is dan ÷(352
+ 202) = ÷1625
Dat is ongeveer gelijk aan 40 meter en 31
centimeter. |
|
|
| Dat het niet beter kan kun je ook nog zien aan
een redenering als de volgende: |
|
|
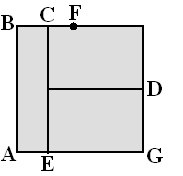
|
Eťn agent moet twee
hoeken nemen, stel A en B. Bovenstaande oplossing gaf AC
= 2÷1625. Als het
efficiŽnter kan, dan moet een andere agent dus C
bewaken.
Maar omdat BD > CD = 2÷1625
moet de derde agent D bewaken (anders is het weer
niet efficiŽnter).
Omdat BE=DE=2÷1625 kunnen de
eerste en derde agent niet E bewaken, dus moet de tweede
dat doen.
Omdat AF > EF = 2÷1625
kunnen de eerste en tweede niet F bewaken, dus moet de
derde dat doen.
Maar G ligt meer dan 2÷1625
van B (eerste), C(tweede) en F(derde) af, dus niemand
kan G bewaken. |
|
|
|
| Vier of Vijf
agenten? |
|
|
| Op een bepaald moment zijn er maar
liefst 5 agenten om het plein te bewaken. Echter de gemeenteraad
wil bezuinigen, en besluit het aantal terug te brengen tot 4.
Men beweert dat 4 agenten net zo effectief zijn als 5, omdat de
maximale afstand van een agent tot een plaats die hij bewaakt
bij 4 agenten niet groter is dan bij 5.
Klopt dat? |
|
 |
|
|
| Eťndimensionaal |
|
|
| Jazeker! er bestaan
ook ťťndimensionale kortste-verbinding problemen. Kijk maar: |
|
|
 |
|
|
In elk van n huizen die
willekeurig langs een rechte weg liggen woont een jongen.
Ergens op deze weg gaan zij elkaar ontmoeten.
Waar moeten zij dat doen om de totale afstand die door alle
jongens samen wordt gelopen naar de ontmoetingsplaats zo klein
mogelijk te maken? |
|
 |
| 3.
Tweedimensionaal in een rooster. |
|
|
|
| Nu wonen er 11 jongens op de
kruisingen in het rooster hiernaast. De roosterlijnen zijn
straten.
Waar kunnen zij elkaar het best ontmoeten?
 |

|
|
|
| 4.
Doorzoek een terrein. |
|
|
|
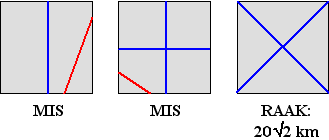
Nog een andere variant, nu weer
tweedimensionaal, is de volgende.
Ergens door een vierkant terrein loopt een kabel ondergronds in
een rechte lijn. Je wilt die kabel opsporen, en weet gelukkig
hoe diep hij ligt.
Je gaat net zolang rechte greppels graven totdat je de kabel
tegenkomt. Dat is niet zo makkelijk. Zie wat pogingen hiernaast.
De blauwe lijnen zijn de gegraven greppels, de rode is de
verborgen kabel. |
|
|
 |
|
|
| Wat is de minimale greppellengte
waarbij je 100% zekerheid hebt de kabel te vinden, en hoe moet
je die greppels graven? |
|
 |