VWO WB12, 2008 - I
Landing

In deze opgave bekijken we een eenvoudig wiskundig model van de baan van een vliegtuig bij de landing.
Een vliegtuig vliegt op een hoogte van 8 km. Op een afstand van 100 km van het vliegveld (horizontaal gemeten) wordt het landingsproces ingezet. We tekenen de baan van het vliegtuig in een assenstelsel: x is de afstand (in km, horizontaal gemeten) vanaf het punt waar het landingsproces wordt ingezet en y is de hoogte (in km). De piloot begint het landingsproces in het punt (0, 8) en het vliegtuig komt in het punt (100, 0) op de grond. Zie de volgende figuur.

De baan die het vliegtuig tijdens het landingsproces beschrijft, wordt in het assenstelsel bij benadering gegeven door: y = 8 − 2,4 • 10−3 • x2 + 1,6 • 10−5 • x3
4p. 1.

Toon langs algebraïsche weg aan dat volgens bovenstaande formule het vliegtuig zowel in het punt (0, 8) als in het punt (100, 0) een horizontale bewegingsrichting heeft.

  

De snelheid in horizontale richting is tijdens het gehele landingsproces 500 km/u. Er geldt dus: x = 500t, waarbij t het aantal uren na het inzetten van de landing is en 0 ≤ t ≤ 0,2.

Voor de hoogte y geldt: y = 8 − 600 • t2 + 2000 • t3.
3p. 2. Toon dit aan.

  

Om veiligheidsredenen mag de absolute waarde van de verticale versnelling   y''(t)   tijdens het landingsproces niet groter zijn dan 1200 km/u2.
4p. 3. Onderzoek of aan deze eis voldaan is.

  

 

Een parabool vouwen

ABCD is een rechthoekig vel papier met daarop een punt F. We vouwen de hoek bij B zo om dat een punt van de rand AB op F komt. Dat kan op allerlei manieren. In onderstaande figuur staan drie voorbeelden.

De vouwlijn noemen we PQ, met P op AB en Q op BC. De plaats van B na het vouwen noemen we B'.

In de bovenste figuur hiernaast is op de rand AB een punt P gekozen.

3p. 4.

Teken zonder te vouwen het bijbehorende punt Q. Licht je werkwijze toe.

  

De vouwlijnen PQ zijn allemaal raaklijn aan één parabool. Zie de tweede figuur hiernaast. Deze parabool heeft brandpunt F en richtlijn AB.


In de derde figuur hiernaast  is één van de vouwlijnen PQ getekend. Deze vouwlijn raakt de parabool in een punt  R.
4p. 5. Teken punt R

  
In de onderste figuur hiernaast  Q het midden van BC.
4p. 6. Bewijs dat ∠BB'C = 90°.

  
Heupoperaties

Patiënten lopen na een operatie in het ene ziekenhuis veel meer gevaar een infectie te krijgen dan in het andere. In het jaar 2003 werden in een bepaald ziekenhuis 120 heupoperaties uitgevoerd, waarna 6 patiënten een infectie kregen. De directie vond het percentage van 5% infectiegevallen te hoog en nam extra preventieve maatregelen. In 2004 werden 154 heupoperaties uitgevoerd, met nu 2 infectiegevallen. Men vroeg zich af of dit betere resultaat toeval was of door de extra preventieve maatregelen kwam.
3p. 7.

Bereken de kans op hoogstens 2 infectiegevallen bij 154 operaties voor het geval dat de kans op infectie per operatie 0,05 is.

  

Omdat de zojuist berekende kans klein is, neemt men aan dat na de extra preventieve maatregelen de kans op infectie na een operatie is afgenomen. De kans op infectie na een operatie na de extra preventieve maatregelen noemen we p.
4p. 8.

Bereken voor welke waarde van p geldt: de kans op hoogstens 2 infectiegevallen bij 154 patiënten is 0,05.

  

De afgelopen vijf jaar was de verpleegduur in Nederlandse ziekenhuizen voor heupoperaties ongeveer normaal verdeeld met een gemiddelde van 4,5 dagen en een standaardafwijking van 1,8 dagen.
Enkele chirurgen hebben de laatste tijd bij heupoperaties een infectieremmend medicijn toegediend. Een zorgverzekeraar beweert dat door behandeling met dit medicijn de gemiddelde verpleegduur korter is dan 4,5 dagen. Men neemt een aselecte steekproef van 100 patiënten die behandeld zijn met het medicijn. Van deze 100 patiënten blijkt de gemiddelde verpleegduur 4,1 dagen te zijn. De standaardafwijking van de gemiddelde verpleegduur van n patiënten is 1,8/√n dagen.
6p. 9.

Onderzoek of door de uitkomst 4,1 dagen de zorgverzekeraar bij een significantieniveau van 5% gelijk krijgt.

  
Een achtkromme

In onderstaande figuur is in een assenstelsel de kromme k getekend, gegeven door

Deze kromme is symmetrisch ten opzichte van de x-as en de y-as.

De kromme k heeft vier punten waarin de raaklijn horizontaal loopt. Deze vier punten zijn de hoekpunten van een rechthoek.
5p. 10. Bereken in één decimaal nauwkeurig de oppervlakte van deze rechthoek.

  

Voor 0 ≤ t ≤ 1/2π geldt dat de coördinaten van de punten van k voldoen aan de vergelijking y = x • √(1− 1/4x2).
4p. 11. Toon dit aan.

  
Vier vragen over f(x) = ln x
De functie f is gegeven door f (x) = lnx.
Het punt E(e, 1) ligt op de grafiek van f. Zie de figuur hiernaast.
De raaklijn in E aan de grafiek van f gaat door O.
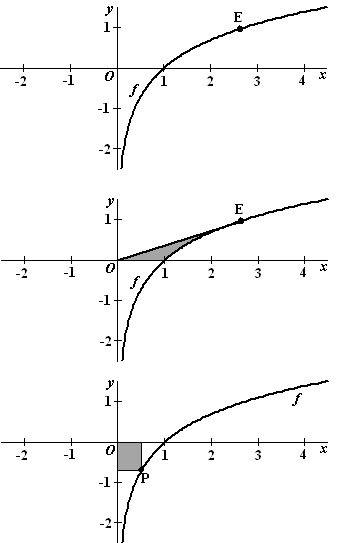3p. 12. Toon dit aan.

  
Het gebied dat wordt ingesloten door de grafiek van f, het lijnstuk OE en de x-as is in de middelste figuur hiernaast grijs aangegeven. Dit gebied wordt gewenteld om de x-as.
4p. 13. Bereken de inhoud van het zo verkregen omwentelingslichaam. Geef je antwoord in twee decimalen nauwkeurig.

  
Voor elke waarde van x met 0 < x < 1 ligt het punt P(x, ln x) op de grafiek van f. We bekijken rechthoeken waarvan twee zijden op de assen liggen en waarvan P een hoekpunt is. Zie de derde figuur hiernaast. Er is een waarde van x waarvoor de oppervlakte van de rechthoek maximaal is.
6p. 14. Bereken langs algebraïsche weg de exacte waarde van die maximale oppervlakte.

  

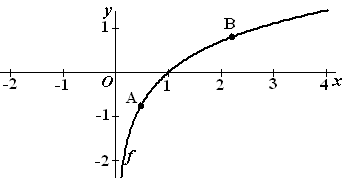
In de onderste figuur zijn op de grafiek van f  twee punten A en B getekend met de volgende eigenschappen:
De y-coördinaten van A en B zijn elkaars tegengestelde. De x-coördinaat van B is 5 keer zo groot als de x-coördinaat van A.
6p. 15.

Bereken de exacte waarde van de x-coördinaat van A.

  

 

De quotiëntrij van de rij van Fibonacci

We beschouwen de rij van Fibonacci: 1, 1, 2, 3, 5, 8, 13, ….
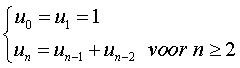
Deze rij wordt beschreven door de formules:

We maken bij de rij van Fibonacci een quotiëntrij door elke term (behalve de eerste) door zijn voorganger te delen:
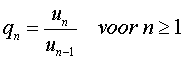
3p. 16. Toon aan dat voor elke n ≥ 2 geldt:

  
De quotiëntrij wordt dus beschreven door de formules

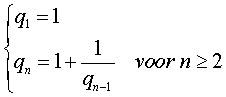
In de volgende figuur zijn de grafieken getekend van y = 1 + 1/x en y = x . Verder is op de x-as de plaats van q1 aangegeven.

3p. 17.

Geef in deze figuur, met behulp van een webgrafiek, op de x-as de plaats van de termen q2 , q3 en q4 van de quotiëntrij aan.
De quotiëntrij heeft een limiet.
4p. 18. Bereken deze limiet exact.

  

 

Twee gelijkzijdige driehoeken

In de volgende figuur zijn twee gelijkzijdige driehoeken ABC en BDE getekend met gemeenschappelijk punt B.

4p. 19. Bewijs dat AE = CD

  

In de onderstaande figuur zijn van de twee gelijkzijdige driehoeken ABC en BDE ook de omgeschreven cirkels getekend. Deze omgeschreven cirkels hebben de punten B en S gemeenschappelijk. Ook zijn de lijnstukken AS en SE getekend.

5p. 20. Bewijs dat hoek ASE een gestrekte hoek is.

  

 

UITWERKINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. Een horizontale bewegingsrichting betekent dat de helling nul is.
De helling is  y' = -4,8 • 10-3 • x + 4,8 • 10-5 • x2
y'(0) = -4,8 • 10-3  • 0 + 4,8 • 10-5 • 0 = 0
y'(100) = -4,8 • 10-3  • 100 + 4,8 • 10-5 • 1002 = 0
Beiden inderdaad nul.
2. y = 8 - 2,4 • 10-3 • x2 + 1,6 • 10-5 • x3 =
8 - 2,4 • 10-3 • (500t)2 + 1,6 • 10-5 • (500t)3 =
8 - 2,4 • 10-3 • 5002 • t2 + 1,6 • 10-5 • 5003 • t3 =
8 - 600t2 + 2000t3
3. y' = -2 • 600t + 3 • 2000t2 = -1200t + 6000t2
y'' = -1200 + 2 • 6000t = -1200 + 12000t
Dat is een lineair verband dus de eventuele maxima en minima zullen aan het begin en/of het eind zitten.
y''(0) = -1200  en  y''(0,2) = 1200
De absolute waarde daarvan is inderdaad niet groter dan 1200.
4. PQ deelt hoek BPF doormidden (want de hoeken BPQ en FPQ lagen oorspronkelijk op elkaar dus zijn gelijk)
Teken de bissectrice van hoek BPF, en waar die BC snijdt ligt punt Q.
(een leuke constructie van de bissectrice van een hoek met alleen een passer en een liniaal zonder schaalverdeling staat trouwens hier)
5. Noem S de projectie van R op  AB.
Raaklijneigenschap:  De raaklijn maakt gelijke hoeken met FR en RS
Dat betekent dat de raaklijn PQ de bissectrice is van hoek FRS
Spiegel daarom F in PQ; dat geeft punt FD'en dat ligt op RS.
Daarmee is S te vinden:  loodrecht van F' op AB.
R is het snijpunt van SF' met PQ.

6. Als Q het midden is dan is  BQ = CQ.
Maar ook BQ = B'Q
Dus is Q het middelpunt van een cirkel waar B, B'en C op liggen (met straal BQ)
BC is een middellijn van die cirkel dus is hoek BBÇ 90º (Thales) 
7. binomiaal verdeeld met n = 154 en p = 0,05
P(X ≤ 2) = binomcdf(154, 0.05, 2) = 0,015
8. binomcdf(154, X, 2) = 0,05
Y1 = binomcdf(154, X, 2)  en  Y2 = 0,05
window bijv.  Xmin = 0, Xmax = 1, Ymin = 0, Ymax = 0,1
intersect geeft  p = 0,04
9. H0:  μ = 4,5  en  σ = 1,8/√100 = 0,18
H1:  μ < 4,5
meting was  4,1
overschrijdingskans:  P(X < 4,1) = normalcdf(0, 4.1, 4.5, 0.18) = 0,013
dat is kleiner dan 0,05 dus H0 mag verworpen worden:  de zorgverzekeraar krijgt gelijk.
10. y = 0,5  Þ  sin2t = 0,5 Þ  2t = 1/6π + k • 2π  V  2t = 5/6π + k • 2π.
Þ  t = 1/12π + k • π  V  t = 5/12π + k • π
tussen 0 en 2π geeft dat de oplossingen  1/12π,  5/12π,  11/12π,  15/12π
dat geeft resp.:  x = 1.93,  x = 0.52,  x = -1,93  en  x = -0,52
de positieve oplossingen zijn  x = 0,52 en x = 1,93 en de afstand daartussen is ongeveer 1,4
11. y = sin(2t) = 2sint cost   maar  sin2t + cos2t = 1 dus  sin2t = 1 - cos2t  dus  sint = √(1 - cos2 t)
daaruit volgt:
y = 2√(1 - cos2t) • cost  = 2√(1 - 1/4 • (2cost)2 ) • cost  = √(1 - 1/4 • (2cost)2 ) • 2cost = √(1 - 1/4x2) • x
12. stel de raaklijn y = ax + b
f '(x) = 1/x
f '(e) = 1/e = a
De lijn is dus  y = 1/e • x + b
Punt (1, e) moet er op liggen:  e = 1/e • x + b  geeft  b = 0
Dus gaat de lijn door de oorsprong.  
13. Wentel de rechte lijn van 0 tot e om de x-as en trek daar de inhoud van de grafiek van f tussen 1 en e gewenteld om de x-as van af:

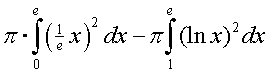Y1 = (1/e • x)2 en dan calc - integraal van 0 tot e geeft 0,90609
Y1 = (ln(x))2 en dan calc - integraal van 1 tot e geeft  0,71882
de inhoud is dan  π • (0,90609-0,71828) = 0,59
14. de oppervlakte is gelijk aan O = -x • lnx
de is maximaal als de afgeleide nul is:  O' = -1 • lnx - x • 1/x = -lnx - 1   (productregel)
-lnx - 1 = 0  ⇒  lnx = -1  ⇒  x = e -1 = 1/e
Dat geeft O = -1/e • ln(1/e) = 1/e  
voor het bewijs dat het inderdaad een maximum is zouden we nog een tekenbeeld van O' moeten maken.
dat ziet er ongeveer zó uit:    (0)+++++(1/e)------(1)
15. Noem de x-coördinaat van A gelijk aan p.
Dan geldt  xB = 5p
yA = lnp  en  yB = ln(5p)
die zijn tegengesteld, dus moet gelden  lnp = -ln(5p) = -(ln5 + lnp) = -ln5 - lnp
 ⇒  2lnp = -ln5 Þ  lnp = -0,5ln5 = -ln√5 = ln(1/√5)
 ⇒  p = 1/√5 
16.
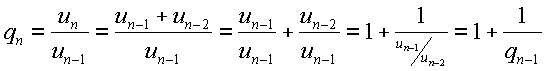
17. hiernaast
Ga steeds van een  q naar de grafiek van 1 + 1/x,
Dan naar de lijn y = x en daar vind je op de x-as de volgende q

18. Die limiet is het snijpunt van beide grafieken:  x = 1 + 1/x
Þ  x2 = x + 1  Þ  x2 - x - 1 = 0 
De ABC-formule geeft de oplossingen  x = (1 + √5)/2 = 1/2 + 1/2√5  en   x = (1 - √5)/2 = 1/2 - 1/2√5 
De oplossing moet positief zijn, dus dat is de eerste:  x = 1/2 + 1/2√5
19. AB = BC want beiden van een gelijkzijdige driehoek
DB = EB want beiden van een gelijkzijdige driehoek.
De driehoeken AEB en CDB zijn congruent want ze hebben twee zijden plus ingesloten hoek gelijk (de hoek is voor beiden 60 + α)
Dus is AE = CD.

q.e.d.

20. ∠ASC = ∠ABC want beiden zijn de omtrekshoek van AC.
Dus ∠ASC = 60º
 ∠BSC = ∠BAC want beiden de omtrekshoek van BC
Dus ∠BSC = 60º
 ∠BSE = ∠BDE want beiden de omtrekshoek van BE
Dus ∠BSE = 60º
 ∠ASE = ∠ASC + ∠BSC + ∠BSE = 60º + 60º + 60º = 180º
Dus ∠ASE is gestrekt.

q.e.d.