|
|
 |
De toets van Wilcoxon.
- ook wel de
Mann-Whitney-toets- |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
Je zou het misschien niet zeggen,
want ik vind hem er eerlijk gezegd niet al te snugger uitzien, maar Frank Wilcoxon hiernaast bedacht
een toets om twee series metingen met elkaar te vergelijken.
We zagen dat vergelijken van twee series metingen ook al bij de
tekentoets, maar daar ging steeds het om paarsgewijze
metingen. Bij deze toets is dat niet meer zo. Sterker nog: beide groepen
die met elkaar vergeleken worden hoeven niet eens even groot te zijn!
Sorry Frank, ik neem mijn opmerking van hierboven terug...
(Wilcoxon ontwikkelde de toets oorspronkelijk in 1945 voor twee
even grote groepen, en de statistici Mann en Whitney maakten later een
uitbreiding voor groepen van ongelijke grootte).
In de toets van Wilcoxon worden twee series getallen met elkaar
vergeleken, waarbij de vraag is: welke serie levert de grootste waarden?
Wilcoxon bedacht iets slims voor een groep van n getallen en een
groep van m getallen.
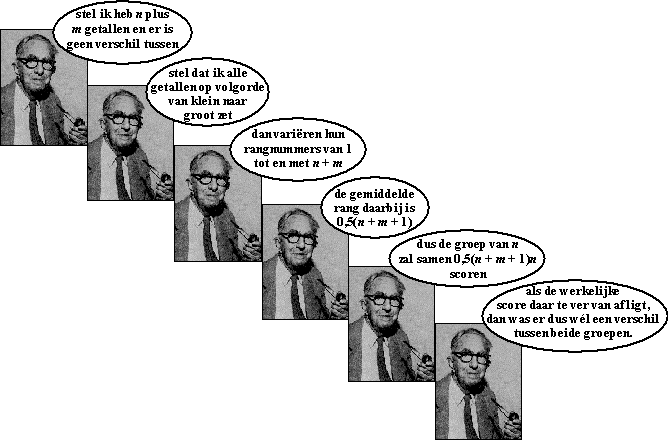
Frank is een grage prater dus ik laat hem
graag zelf aan 't woord: |
 |
| |
|
|
 |
| |
|
Eigenlijk zegt hij dus:
Stel dat er geen verschil is: H0
Dan is de verwachtingswaarde voor de som van de rangnummers van de groep
van n gelijk aan 0,5n(n + m + 1).
Als de meting daar te ver naast zit, dan is er wél verschil.
Voorbeeld.
Stel ik heb twee series getallen. Serie
1: 2-6-8-10-12 en Serie
2: 3-4-5-9-11-16-17-20
Zet de series op volgorde van kleine naar groot en geef ze een
rangnummer: |
| |
|
| getal |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
12 |
16 |
17 |
20 |
| rang |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
| |
|
de totale rang van de kleinste
groep (de blauwe) is 1 + 5 + 6 + 8 + 10 =
30
De verwachte totale score van die groep zou moeten zijn
0,5n(n + m + 1) = 0,5 • 5 • (5 + 8+ 1) = 35
De grote vraag is nu: verschilt die 30 genoeg van de verwachte 35
om dit als een significant verschil te zien?
Als je intussen iets van de vorige lessen over toetsen hebt begrepen,
dan zul je vast wel snappen dat het gaat om de vraag: Hoe groot is
de kans op een minstens even grote afwijking? Juist! De
overschrijdingskans!!
In het geval van de toets van Wilcoxon onderscheiden we nu twee
gevallen. |
| |
|
| GEVAL
1: Kleine steekproeven. |
|
| |
|
We noemen een steekproef klein
als één van beide (of beide) groepen klein is
| |
| kleine steekproef: n
≤ 4
of m
≤
9 |
|
| |
Voor kleine steekproeven kun je die overschrijdingskans eigenlijk
alleen maar berekenen door alle mogelijkheden uit te schrijven.
|
Voorbeeldberekening.
Stel; dat de kleinste groep uit twee getallen KK bestaat en de grootste
groep uit 5 getallen GGGGG.
Dan staan in de tabel hiernaast alle 21 (7 nCr 2) mogelijke
volgorden, met daarbij de score voor de kleinste groep.
Dat geeft de volgende kansen voor de scores van de kleinste groep:
| score S |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| aantal keer |
1 |
1 |
2 |
2 |
3 |
3 |
3 |
2 |
2 |
1 |
1 |
| kans |
0,047 |
0,047 |
0,095 |
0,095 |
0,143 |
0,143 |
0,143 |
0,095 |
0,095 |
0,047 |
0,047 |
| cumulatief |
0,047 |
0,095 |
0,190 |
0,286 |
0,429 |
0,571 |
0,714 |
0,910 |
0,905 |
0,952 |
1,000 |
Als we te maken hebben met
α = 0,05 dan
zie je dat alleen de scores van 3 en 13 significant zijn (kans
0,047).
Dus bij n = 2 en m = 5 is er met
α
= 0,05 alleen bij een score van 3 of 13 voor de kleinste groep te
concluderen dat H0 verworpen mag worden.
Nou kun je je voorstellen dat voor grotere waarden van n en m
het nogal veel werk wordt om deze tabel te maken en de kans op alle
scores te bepalen.
Gelukkig is dat voor je gedaan.
Het resultaat staat in de volgende tabel.
|
| volgorde |
score n-groep |
| KKGGGGG |
3 |
| KGKGGGG |
4 |
| KGGKGGG |
5 |
| KGGGKGG |
6 |
| KGGGGKG |
7 |
| KGGGGGK |
8 |
| GKKGGGG |
5 |
| GKGKGGG |
6 |
| GKGGKGG |
7 |
| GKGGGKG |
8 |
| GKGGGGK |
9 |
| GGKKGGG |
7 |
| GGKGKGG |
8 |
| GGKGGKG |
9 |
| GGKGGGK |
10 |
| GGGKKGG |
9 |
| GGGKGKG |
10 |
| GGGKGGK |
11 |
| GGGGKKG |
11 |
| GGGGKGK |
12 |
| GGGGGKK |
13 |
|
| N.B.
Bedenk goed dat in deze tabel de grenswaarden staan waarbij H0
nog nét WEL verworpen mag worden. |
| |
|
GEVAL 2: Grotere steekproeven. |
| |
Grote steekproeven zijn alle
steekproeven die niet kleine zijn:
| |
|
grote steekproef : n
≥
5 én m
≥ 10 |
|
|
|
Bij grotere steekproeven is het uitvoeren van de toets minder werk,
omdat de som van alle scores in dat geval benaderd kan worden door een
normale verdeling.
• De verwachtingswaarde m daarvan
kennen we natuurlijk al:
μ = 0,5n(n
+ m + 1).
• De standaarddeviatie is niet zomaar te verzinnen. De formule
daarvan is
σ = √(1/6
• μ • m)
Als je deze formules eenmaal weet is het verder een makkie: net zoals
bij de z-toets bereken je de overschrijdingskans van de score van
de kleinste groep.
Denk daarbij wel aan de
continuïteitscorrectie!
Je benadert immers hier scores met een normale verdeling terwijl je wéét
dat het alleen gehele getallen kunnen zijn.
Voorbeeld.
Twee groepen bestaan uit de volgende waarden:
Groep 1: 4 - 6 - 7 - 15 - 18 - 25
Groep 2: 1 - 3 - 5 - 12 - 16 - 19 -
24 - 26 - 30 - 32
Is er verschil of niet? Neem a = 0,10
Het geeft de volgende scores:
| waarde |
1 |
3 |
4 |
5 |
6 |
7 |
12 |
15 |
16 |
18 |
19 |
24 |
25 |
26 |
30 |
32 |
| score |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
De totale score van de blauwe groep is 3 + 5 + 6 +
8 + 10 + 13 = 45
μ = 0,5n(n + m + 1) = 0,5 • 6 • (6 + 10 + 1) = 51
σ = √(1/6
• m • m) =
√(1/6
•
51 • 10) = 9,2195
De meting is 45.
Dus de overschrijdingskans is normalcdf(0, 45.5, 51, 9.2195)
= 0,275
Dat is veel groter dan
α
(0,10), dus de conclusie is: H0
aannemen: er is géén significant verschil. |
| |
|
Daar zijn ze weer: de punten van
aandacht! |
| |
|
1. Verdelingsvrij
Net als een tekentoets is ook deze toets
verdelingsvrij. Dat betekent dat het niet uitmaakt hoe de
getallen precies verdeeld zijn. Er hoeft niet te worden voldaan aan
bijvoorbeeld een normale verdeling of zoiets. De eigenlijke verdeling
doet er niet toe; we maken er immers zélf gewoon een nieuwe verdeling
van.
2. Als de getallen gelijk zijn?
Waarschijnlijk had je deze oplossing zelf wel verzonnen: dan verdeel je
de scorepunten. Als bijvoorbeeld twee getallen samen op de plaatsen 4 en
5 staan, dan krijgt elk als score 4,5.
En als er vijf getallen samen op de plaatsen 5, 6, 7, 8 en 9 staan
krijgt elk dus score 7.
3. Zijn er verder nog voorwaarden?
Het is niet zo héél belangrijk, maar de toets gaat er wel van uit dat de
verdelingen van beide getallenseries gelijk zijn. Nou is
dat eigenlijk altijd wel zo omdat je nou eenmaal gelijke dingen met
elkaar vergelijkt. |
| |
|
| |
|
|
OPGAVEN |
| |
|
| |
| 1. |
Het vermoeden bestaat dat studenten in Groningen
meer bier drinken dan studenten in Amsterdam.
Men onderzocht van een aantal studenten hoeveel glazen bier zij
gemiddeld in een week consumeerden.
Dat gaf de volgende resultaten.
De bierconsumptie van de Amsterdamse studenten was:
36, 14, 55, 32, 58, 28, 20, 32, 32, 8, 37, 38, 42, 47, 18, 25
De bierconsumptie van de Groninger studenten was:
16, 65, 31, 63, 35, 41, 60, 51, 44, 34, 64, 26
Is er naar aanleiding van deze gegevens reden om aan te nemen
dat Groninger studenten inderdaad meer bier drinken dan
Amsterdamse? Neem
α = 0,05. |
| |
|
|
|
| 2. |
Een onderzoeker wil weten of bij het leren lopen van kinderen
jongens of meisjes eerder los kunnen lopen.
Zes onderzocht meisjes liepen voor het eerst los toen ze 350 –
390 – 435 – 440 – 448 – 455 dagen oud waren.
Acht onderzochte jongens liepen voor het eerst los toen ze 360 –
388 – 400 – 410 – 430 – 442 – 450 – 462 dagen oud waren.
Welke conclusie kun je bij een significantieniveau van 5%
trekken uit deze gegevens? |
| |
|
|
|
| 3. |
De CITO scores van kinderen van groep 8 van een
klein schooltje waren als volgt onder de meisjes en de jongens
verdeeld:
Meisjes: 540 – 538 – 536 – 549 - 520
Jongens: 510 – 523 – 523 – 535 - 537
Onderzoek of deze cijfers aanleiding geven te zeggen dat de
meisjes beter scoorden dan de jongens. Neem een
significantieniveau van 5%. |
| |
|
|
|
| 4. |
Er wordt wel eens beweerd dat het inkomen van
mensen die in een stad wonen groter is dan dat van mensen die op
het platteland wonen. Men wil deze bewering toetsen met een
α = 0,05.
Een willekeurige steekproef leverde de volgende tabel: |
| |
|
|
|
| |
| Inkomen |
50200 |
45000 |
63500 |
75000 |
90000 |
84600 |
64000 |
98000 |
67000 |
| Stad/Platteland |
P |
S |
S |
S |
S |
S |
P |
S |
P |
|
| |
|
| |
| Inkomen |
40900 |
60000 |
73400 |
87200 |
88000 |
93000 |
94500 |
81000 |
70400 |
| Stad/Platteland |
P |
P |
S |
S |
S |
P |
S |
P |
S |
|
| |
|
|
|
| |
Een statisticus voert deze gegevens
in, en meet voor de hele groep een gemiddelde van 73650 en een
standaarddeviatie van 16858.
De plattelandsmensen hebben een gemiddeld inkomen van 65157.
De statisticus toetst nu H0:
μ = 73650,
σ =16858 tegen H1:
μ
< 73650
Hij meet een gemiddelde van 65157 en zegt:
normalcdf(0,65157,73650,16858) = 0,307 dus H0 moet
worden aangenomen. |
| |
|
|
|
| |
a. |
Leg uit welke fout(en) de statisticus heeft
gemaakt. |
| |
|
|
|
| |
b. |
Voer een correcte toets uit om vast
te stellen of er aanleiding is de veronderstellen dat het
inkomen in de stad groter is dan dat op het platteland. Neem
α = 0,10 |
| |
|
|
|
| 5. |
De omroep BNN organiseert elk jaar
de Nationale IQ test.
Daarbij zijn er ook vijf vakken, elk met een speciaal soort
publiek die meedoen. In 2011 had men bijvoorbeeld de "Oh-Oh-Cherso-fans" en de "Larpers" (dat zijn de
Live-Action-Role-Players).
Het gemeten IQ voor een aantal mensen uit deze twee categorieën
was als volgt:
Larpers: 95 - 100 - 103 - 116 - 123 - 128 - 130
Oh-Oh-Cherso fans: 86 - 99 - 101 - 102 - 112 - 124
Mag je uit deze gegevens concluderen dat Larpers een hoger IQ
hebben dan Oh-Oh-Cherso fans?
Neem een significantieniveau van 5%. |
| |
|
|
|
| 6. |
Een groep van 16 mensen doet een
half jaar lang mee aan een gewichtsverlies-programma.
Na afloop vraagt men zich af of het resultaat van dat programma
voor vrouwen en voor mannen wel gelijk is.
Het gewichtsverlies dat de deelnemers hadden was namelijk als
volgt:
Vrouwen: 14, 14, 25, 20, 19, 16, 17, 20, 13
Mannen: 14, 23, 12, 10, 17, 10, 19
Wat kan men concluderen met
α = 0,05? |
| |
|
|
|
| 7. |
Mix opgave.
Van een groep volwassenen en van een groep kinderen is het
ruimtelijk inzicht gemeten, en dat gaf voor iedereen een score
van 0 tm 100.
Dit waren de resultaten, geordend van laag naar hoog:
Voor de volwassenen de scores: 23, 35, 36, 45, 58,
62, 64, 79, 87, 90.
Voor de kinderen de scores: 15, 19, 26, 35, 38, 59, 60,
63, 82, 88. |
| |
|
|
|
| |
a. |
Bepaal of je aan de hand van deze gegevens met
significantieniveau 5% mag concluderen dat volwassenen een beter
ruimtelijk inzicht hebben dan kinderen |
| |
|
|
|
| |
In
werkelijkheid betrof het hier ouders met hun kinderen. De
scores van een ouder met het bijbehorende kind waren als volgt: |
| |
|
|
|
| |
| ouder |
58 |
35 |
36 |
45 |
23 |
62 |
87 |
79 |
64 |
90 |
| kind |
38 |
26 |
15 |
19 |
63 |
60 |
82 |
88 |
59 |
35 |
|
| |
|
|
|
| |
b. |
Onderzoek opnieuw vraag a). |
|
| |
|
|
|
| |
c. |
Bepaal hoe groot de correlatiecoëfficiënt is tussen het
ruimtelijk inzicht van een ouder en dat van zijn of haar kind.
Bepaal ook welk ouder-kind koppel net grootste residu oplevert
en hoeveel de correlatiecoëfficiënt verbetert als dat koppel als
meetfout wordt gezien. |
| |
|
|
|
| |
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|