Wentelen om de y-as

© h.hofstede (h.hofstede@hogeland.nl)
       
Hiernaast zie je (een deel van) de grafiek van y = √x.
Om precies te zijn het deel voor x tussen 0 en 4.

Als je dat grafiekdeel wentelt om de y-as dan krijg je zoiets als hieronder. In deze figuur is al een dun schijfje (dikte dy) van dit lichaam getekend.

       

       
De inhoud van dat ene schijfje is gelijk aan grondvlak ´ hoogte ('t is immers een cilinder).
Het grondvlak is een cirkel met straal x en de hoogte is dy.  Dat geeft voor de inhoud  px2dy

Voor de hele inhoud van dit omwentelingslichaam moeten we al die schijfjes bij elkaar optellen, en liefst zo dun mogelijk maken. Voel je hem al aankomen.....?  Juist!...... Een integraal.
       

       
Omdat er achter de integraal dy staat is y de variabele waar het om gaat. Dat betekent dat we alle andere variabelen óók moeten uitdrukken in y, en ook dat de grenzen van de integraal y-grenzen zijn.

Als x = 4, dan is y = 2  dus de grenzen zijn  y1 = 0  en  y2 = 2
Rest ons nog om ook die x2 uit te drukken in y.
Omdat de functie is y = √x  geldt  x = y2  dus  x2 = y4

Daarmee gaat de integraal zó:
       
   
 OPGAVEN
   
1. Bereken de exacte waarde van de inhoud van het omwentelingslichaam dat ontstaat als je de volgende vlakdelen wentelt om de y-as:
               
  a. V1, ingesloten door de grafiek van  y = √(2x - 4) en de x-as en de y-as en de lijn y = 2.

1414/15π
  b. V2, ingesloten door de grafiek van  y = ln(2x) en de x-as en de y-as en de lijn y = 1.

1/8π(e2 - 1)
  c. V3, ingesloten door de grafiek van  y = 1/2x3 en de x-as en de lijn x = 2.

9,6π
  d. V4, ingesloten door de grafiek van  y = 2/(x + 1) - 1   en de y-as en de x-as.

3 + 4ln2
               
2. De grafieken van y = ³√x en   y = 1/2x  snijden elkaar voor x ≥ 0   in   (0,0) en in (√8, √2)
Ze sluiten voor x ≥ 0  samen een vlakdeel V in.
Je kunt V  wentelen om de x-as, maar natuurlijk ook om de y-as. In beide gevallen krijg je een omwentelingslichaam
               
  a. Toon aan dat beide grafieken inderdaad door  (√8, √2) gaan
               
  b. Kun je zonder een berekening te maken voorspellen welk van die beide omwentelingslichamen de grootste inhoud zal hebben?
               
  c. Controleer je antwoord op vraag b) door van  beide omwentelingslichamen de inhoud in twee decimalen nauwkeurig te berekenen.
           

4,74 en 6,77
  d. Bereken beide inhouden exact.
           

16/15π√2 en 32/21π√2
               
3. V is het vlakdeel, ingesloten door de grafiek van y = 1/(x + 2) en de x-as en de y-as en de lijn x = 4
Bereken de  inhoud van het omwentelingslichaam dat ontstaat als V wordt gewenteld om de y-as.
       
  a. Afgerond op twee decimalen.

11,33
  b. De exacte waarde.

π(8 - 4ln3)
 
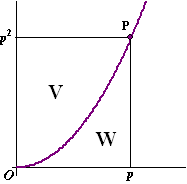
4. Op de grafiek van y = x2  kiezen we een punt P met coördinaten (p, p2)
Teken ook de projecties van P op de coördinaatassen. Dat geeft twee vlakdelen.
V wordt ingesloten door de grafiek van f en de y-as en
de lijn y = p2
W wordt ingesloten door de grafiek van f, de x-as en
de lijn x = p
We wentelen V om de y-as en W om de x-as.

Voor welke p zijn de inhouden van de lichamen die we dan krijgen gelijk?

     

p = 2,5
       
5. Gegeven zijn de functies:  f(x) = √(x + 3)  en  g(x) = x2 - 9 op het domein [-3, 0]
       
  a. Bereken de oppervlakte van het vlakdeel V dat ingesloten wordt door de grafieken van f en g en de y-as
     

 
  b. Bereken de inhoud van het omwentelingslichaam dat ontstaat als vlakdeel V wordt gewenteld om de y-as.
       
       
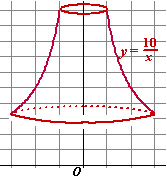
6. Het deel van de grafiek van y = 10/x tussen x = 1 en x = 3 wordt gewenteld om de y-as. Daarbij ontstaat een soort vaas, zoals je hiernaast ziet.

Bereken de exacte waarde van de inhoud van deze vaas.
     

20π
       
7. Gegeven is de functie  f(x) = 1/(x + 1)

De lijn y = 0,5 en de y-as en de grafiek van f sluiten een vlakdeel V in.
       
  a. Bereken algebraïsch de oppervlakte van V.
     

ln2 - 0,5
  b. Vlakdeel V wordt gewenteld om de y-as.  Bereken algebraïsch de inhoud van V.
     

π(1,5-2ln2)
       
8. Het vlakdeel in gesloten door de grafieken van  y = 2√(x - 1) en  y = x - 1  wordt gewenteld om de lijn x = -1.
Bereken algebraïsch de inhoud van het omwentelingslichaam dat dan ontstaat.
     

191/5π
9. Examenopgave VWO, Wiskunde B, 2019- II
       
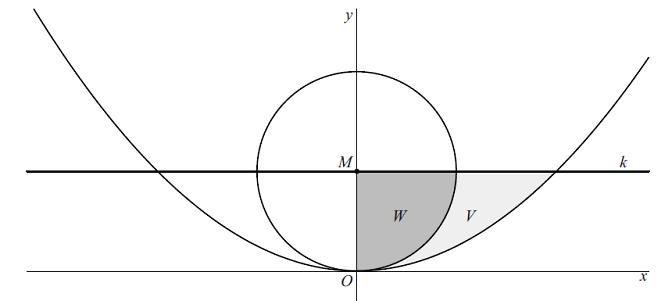
  Gegeven zijn de parabool  y = x2  en de cirkel met middelpunt M(0, r) en straal r.

De lijn k gaat door M en is evenwijdig aan de x-as. V is het gebied rechts van de y-as dat wordt ingesloten door de cirkel, de parabool en lijn k. In onderstaande figuur is dit gebied lichtgrijs gemaakt.
W is het gebied rechts van de y-as dat wordt ingesloten door de cirkel, de y-as en lijn k. In de figuur is dit gebied donkergrijs gemaakt.
       
 

       
 

Wanneer de cirkel wordt gewenteld om de y-as, ontstaat een bol met inhoud 4/3πr3

De gebieden V en W worden gewenteld om de y-as.
Er is een waarde van r waarvoor de inhoud van de omwentelingslichamen van V en W aan elkaar gelijk zijn.

Bereken exact deze waarde van r.
     

r = 3/8
10. Examenopgave VWO, Wiskunde B, 2021- III

De functie f wordt gegeven door f(x) = x3 + 6x2 + 12x + 9
Deze functie heeft een inverse functie f inv .
Er geldt:
 

       
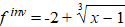  a. Toon dit aan.  
       
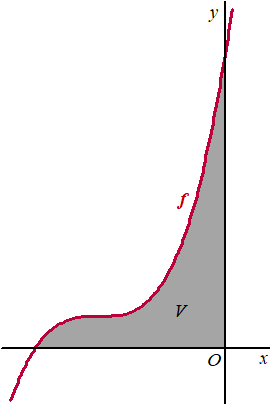
  V is het vlakdeel dat wordt ingesloten door de grafiek van f, de x-as en de y-as. Zie de figuur. Deze figuur is niet op schaal.
       
 

       
  Vlakdeel V wordt gewenteld om de y-as. Zo ontstaat een omwentelingslichaam.
       
  b. Bereken de inhoud van dit omwentelingslichaam. Geef je eindantwoord in één decimaal.
     

33,9
     

© h.hofstede (h.hofstede@hogeland.nl)