Wentelen om de x-as.

© h.hofstede (h.hofstede@hogeland.nl)

Bekijk een vlakdeel onder de grafiek van een willekeurige functie.
Hiernaast is als voorbeeld de functie f(x) = x3 - 7x2 + 12x + 6 genomen, tussen x = 0 en x = 5
Als je dat vlakdeel om de x-as wentelt, dan krijg je een soort van "vaas". De vraag is:  Hoe groot is de inhoud van die vaas?
Laten we de vaas in allemaal kleine schijfjes snijden

Eén zo'n schijfje is ongeveer een cilinder met hoogte dx en straal r, dus inhoud  πr2 • dx

Maar nu komt de verrassing: r is gelijk aan de hoogte van de grafiek:

r = f (x)
De totale inhoud is nu de integraal van al die schijfjes:

Dit is een handige formule, want hij geldt nog steeds voor elke willekeurige functie f.
Kortom, onthoud deze formule:

Toegepast op onze vaas moeten we integreren tussen x = 0 en x = 5.
't Is met dat kwadraat wél even stug haakjes wegwerken:
f 2 = (x3 - 7x2 + 12x + 6) • (x3 - 7x2 + 12x + 6)
= x6 - 7x5 + 12x4 + 6x3 - 7x5 + 49x4 - 84x3 - 42x2 + 12x4 - 84x3 + 144x2 + 72x + 6x3 - 42x2 + 72x + 36
= x6 - 14x5 + 73x4 + -156x3 + 60x2 + 144x + 36
Dat geeft:


Dat is ongeveer 1358.
   
  OPGAVEN
1. a. De parabool  y = 4x - x2  wordt tussen x = 0 en x = 4 gewenteld om de x-as.
Bereken algebraïsch de inhoud van het omwentelingslichaam dat zo ontstaat.

512/15π
       
b. De halve cirkel   y = √(16 - x2)  wordt gewenteld om de x-as.
Bereken algebraïsch de inhoud van de bol die zo ontstaat. 
Laat zien dat voor die inhoud geldt  I = 4/3πr3
     

851/3π
c. Het deel van de grafiek y = 6 - √x tussen x  = 0 en x = 36  wordt gewenteld om de x-as. Bereken algebraïsch de inhoud van het omwentelingslichaam dat zo ontstaat.

216π
2. Het vlakdeel, ingesloten door de grafieken van y = x3 en y = x   met x > 0 wordt gewenteld om de x-as. Bereken algebraïsch de inhoud van het omwentelingslichaam dat zo ontstaat.
     

4/21π
3.

Gegeven zijn de functies:     f(x) = x • √x   en    g(x) = ax

V is het vlakdeel dat ingesloten wordt door de grafieken van f en g.
Als V om de x-as gewenteld wordt, dan is de inhoud van het omwentelingslichaam dat dan ontstaat gelijk aan 211/3π.
Bereken in dat geval het getal a.
     

a = 2
4. Voor de inhoud van een kegel geldt de formule  I = 1/3 • pr2 • h  (r is de straal van de grondcirkel en h de hoogte).
Maar een kegel kun je als omwentelingslichaam zelf maken door een recht lijnstuk door de oorsprong 
tussen x = 0 en x = h te wentelen om de x-as.
Bewijs op deze manier de inhoudsformule hierboven. 
       
Voor de volgende drie opgaven moet je weten dat de vergelijking van een cirkel met straal r en middelpunt de oorsprong is:   y2 = r2 - x2
5.

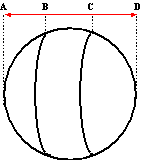
Wij hebben met z'n tweetjes een heerlijk bolletje brood (diameter12) dat we samen moeten delen. Jij stelt voor om het bolletje langs twee verticale cirkels door te snijden in drie "gelijke" stukken (dus AB = BC = CD = 4). Ik zal de beide buitenste stukken krijgen, jijzelf neemt het middenstuk

Wie krijgt het meeste brood?

     
6. Een enorm cognacglas bestaat uit een bol met diameter 10 cm. De opening aan de bovenkant is een cirkel met diameter 6 cm.
     
 

     
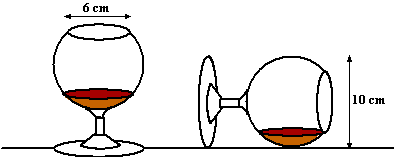  Als je het glas helemaal vol zou schenken dan gaat er maar liefst ongeveer 0,51 liter in!
Een goede barkeeper schenkt er echter maar een klein laagje cognac in. Het moet precies zoveel cognac zijn, dat het er nét niet uitloopt als je het glas op zijn kant legt. Zie de tekening rechts.

Bereken met een integraal hoeveel cognac er in een goed-ingeschonken glas zit.
   

14,67 cm3

   
7. Een beroemd raadsel gaat als volgt:

Midden door een bol wordt een cilindervormig gat geboord.
De hoogte van de cilinder na het boren is 10 cm.
Bereken de inhoud van het overblijvende gedeelte van de bol.
  Het lijkt erop alsof je te weinig informatie hebt, want de straal van de bol is niet gegeven, en ook de straal van het gat niet.  Maar schijn bedriegt!

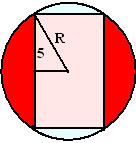
De situatie is in de doorsnede hiernaast geschetst. Het felrode deel is wat er van de bol is overgebleven. Je ziet dat er in totaal een cilinder met hoogte 10 (lichtrood) plus twee kapjes (lichtblauw)  van de bol zijn weggehaald.

Los met deze figuur het beroemde raadsel op. 
(Leg daarvoor de bol in een assenstelsel met het gat in de richting van de x-as, en bereken de inhoud van de cilinder en van beide kapjes).

   

1662/3π
     
8. V is het vlakdeel dat wordt ingesloten door de grafiek van f(x) = 9 - x2, de y-as en de positieve x-as.
De lijn x = a verdeelt V in twee delen V1 en V2.
     
  a. Bereken voor welke a de oppervlakten van V1 en V2 gelijk zijn. Geef je antwoord in drie decimalen nauwkeurig.
     

1,042
  b. V1 en V2 wentelen om de x-as. Zo ontstaan de lichamen L1 en L2.
Bereken voor welke a de inhouden van L1 en L2 gelijk zijn. Geef je antwoord in drie decimalen nauwkeurig.
   

0,843
     
9. Gegeven zijn de functies  f(x) = x2 - 6x   en    g(x) = -x3
     
  a. V is het vlakdeel in gesloten door de grafiek van f en de x-as. V wordt gewenteld om de x-as.
Bereken de inhoud van het omwentelingslichaam dat zo ontstaat.
   

259,2π
  b. Bereken exact de totale gezamenlijke oppervlakte van de twee vlakdelen, ingesloten door de
grafieken van f en g.
   

253/12
  c. De lijn y = -ax (met a > 0) en de grafiek van g sluiten ook een vlakdeel in, waarbij x > 0.
Bereken voor welke a de oppervlakte van dit vlakdeel gelijk is aan 9.
   

a = 6
     
10. Voor  0 ≤ x ≤ 4 is gegeven de functie  f(x) =  2/(2x + 3)
Het gebied G wordt ingesloten door de x-as en de grafiek van f en de lijnen x = 0,5  en x = 2,5
     
  a. Bereken exact de oppervlakte van gebied G. Schrijf je antwoord als één logaritme.
   

ln2
  b. Bereken door middel van integreren de inhoud van het lichaam L dat ontstaat door gebied G te wentelen rond de x-as.
   

0,5π
  c. Er zijn twee waarden van p waarvoor de lijn y = -x + p de grafiek van f raakt.
Bereken die twee waarden.  
   

0,5 en -3,5
     

© h.hofstede (h.hofstede@hogeland.nl)