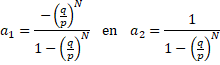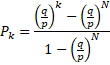© h.hofstede (h.hofstede@hogeland.nl)

Een Stochastische Wandeling....
       
Een deeltje bevindt zich op de getallenlijn en neemt stappen van 1 of -1  (dus 1 naar rechts of 1 naar links). Om iedere stap wordt geloot (daarom heet dit een stochastische wandeling). Stel dat de kans op 1 gelijk is aan p en op -1 gelijk aan q.
Het deeltje begint in punt k.
Als het deeltje punt 0 of punt N bereikt is de wandeling afgelopen.
Daarom heet dit officieel een stochastische wandeling met absorberende grenzen.

Toepassing natuurlijk:
Een speler speelt een spel om inzet 1 (bijvoorbeeld in een casino). Zijn beginkapitaal is k. Als hij N  heeft stopt hij ermee, als hij 0 heeft moet hij wel stoppen.....

Stel  P0 is de kans dat de speler uiteindelijk in 0 gaat belanden een PN is de kans dat de speler uiteindelijk in N gaat belanden. "Uiteindelijk"  kan na een willekeurig aantal stappen zijn... dat is nog niet bekend....
       
Conditioneren.
       
We gaan nu een methode uitvoeren die heet  "Conditioneren naar een stelsel S1, S2, ...." Daarbij zijn de Si een aantal gebeurtenissen die geen doorsnede hebben (dat heet disjunct) en die samen kans 1 hebben (dat heeft volledig).
Het idee is het volgende:  (hier volgt een beetje een dom voorbeeldje)

Stel dat ik wil uitrekenen wat de kans is dat ik met een dobbelsteen 6 gooi.
Dan neem ik het stelsel gebeurtenissen    S1= het is maandag,  S2 = het is dinsdag,  S3 = het is een andere dag.
De kans dat ik zes gooi is nu:
P(6) = P(maandag) • P(6\maandag) + P(dinsdag) • P(6\dinsdag) + P(andere dag) • P(6\andere dag)
= 1/7 • 1/6 + 1/7 • 1/6 + 5/7 • 1/6
= 1/6.
Ik splits die kans op 6 eigenlijk over de S-mogelijkheden. Heeft bijvoorbeeld als voordeel dat ik nu ook de kans op 6 kan uitrekenen als ik bijvoorbeeld weet dat ik op maandag vaker zes gooi dan de andere dagen.
In formule:

       
Terug naar onze wandeling....
Ik ga nu de kans dat ik 0 bereik berekenen als ik begin in k.  Die kans noem ik Pk(nul), en die ga ik splitsen naar de gebeurtenissen S:   S1 = eerste stap is PLUS en  S2 = eerste stap is MIN
Dat geeft:  
Pk(nul) = P(PLUS) • P(nul\PLUS) + P(MIN) • P(nul\MIN)
Pk(nul) = p • P(nul\PLUS) + q • P(nul\MIN)

Maar nu zijn er drie gevallen, afhankelijk van waar je begint op de lijn:  k = 1,  k = N - 1 , of k = "de rest"
Immers als je in 1 begint en je neemt een stap naar links ben je al in nul,  en als je in N-1 begint en je neemt een stap naar rechts kun je nooit meer 0 bereiken.

k = 1  geeft:   P1(nul) = p • P2 + q • 1 
k = N - 1  geeft  PN - 1(nul) = q • PN - 2  + q • 0
k = "de rest"   geeft  Pk(nul) = p • Pk + 1 + q • Pk - 1     (dus voor   k =  2, ...., N - 2)

Dit is een stelsel van N - 1 vergelijkingen met N - 1 onbekenden (de Pk) dat ten hoogste één oplossing heeft.

Waarom ten hoogste één oplossing?

Het stelsel  ziet er voor N = 10 bijvoorbeeld zó uit:
       
P1 = pP2 + q
P2 = p P3 + qP1
P3 = pP4 + qP2
P4 = pP5 + qP3
P5 = pP4 + qP6
P6 = pP5 + qP7
P7 = pP6 + qP8
P8 = pP7 + qP9
P9 = qP8
       
Begin onderaan en werk omhoog:  P8 = 1/qP9,  en dan  P7 = 1/p(P8 - qP9) = 1/p(1/qP9 - qP9),  en dan P6 = ....... enzovoort
Zo kun je alle P's uitdrukken in P9
Als je dat allemaal tot de bovenste hebt gedaan komt het spannende moment van invullen in die eerste vergelijking.
Dat geeft een oplossing of niet.
Maar er is in ieder geval ten hoogste één oplossing!

Probeer Pk = a • ck 
Dat geeft  voor de middenvergelijkingen:  
Pk(nul) = p • Pk + 1 + q • Pk - 1
a • ck = p • a • ck + 1+ q • a • ck - 1   deel alles door a • ck - 1 
c = pc2 + q
pc2 - c + q  = 0

We onderscheiden nu twee gevallen:

Geval 1:  p ≠ q
  Dan heeft deze vergelijking twee oplossingen; c = 1  en   c = q/p   (bedenk dat p + q = 1)
De oplossingen zijn dus  Pk = a  en  Pk = a • (q/p)k  waarbij die a's willekeurig zijn, en niet gelijk hoeven te zijn.
Aan de middenvergelijkingen is voldaan door een willekeurige combinatie van deze twee:
Pk = a1 + a2(q/p)k  
Nu gaan we die a1 en a2 zo kiezen dat ook aan de buitenste twee vergelijkingen wordt voldaan.
Dat geeft:
 

  En de oplossing is dus 
 

       
Geval 2:  p = q = 0,5
  Dan heeft de vergelijking een dubbele wortel c = 1, maar nu voldoet ook Pk = k aan de middenvergelijkingen.
De algemene oplossing is dan  Pk = a1 + a2 • k
De beide randvergelijkingen geven dan a1 = 1  wen  a2 = -1/N 
De algemene oplossing is dan  Pk = 1 - k/N  
       
Voorbeeld.
Hans en  Loes spelen een spel; ze gooien een dobbelsteen, en als er 1 of 2 gegooid wordt, dan geeft Hans een euro aan Loes. Als er 3, 4, 5, of 6 gegooid wordt geeft Loes een euro aan Hans.
Hans begint met  €10  en Loes met €15
Hoe groot is de kans dat  Hans blut raakt?

Je herkent uiteraard de wandeling met (vanuit Hans geredeneerd)  N = 25, k = 10,  p = 1/3 en q = 2/3
Invullen:   P10 = (210 - 225)/(1 - 225) =  0,9999695122....
       
       

© h.hofstede (h.hofstede@hogeland.nl)