| |
 |
| Voorspellingen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
Als we aan de hand van een puntenwolk een
regressielijn van x op y hebben opgesteld, dan kunnen we
die lijn natuurlijk gebruiken om van nieuwe x-waarden de
bijbehorende y te voorspellen. (We zagen al eerder dat het
regressie-effect er daarbij voor zorgt dat extremen waarden een
voorspelling opleveren die "meer naar het gemiddelde" toe ligt.).
De vraag is nu eigenlijk:
| |
| Hoe betrouwbaar zijn
die voorspellingen? |
|
| Het zal je hopelijk intussen duidelijk zijn dat bij hoge
(positieve of negatieve) correlatie, de voorspellingen betrouwbaar zijn,
en bij lage correlatie onbetrouwbaar. Bij hoge correlatie liggen de
gemeten punten bijna op een rechte lijn, en zal de voorspelling daar
waarschijnlijk ook weinig van afwijken. |
Maar hoe goed is nou zo'n voorspelling?
Hůe hangt de nauwkeurigheid van r af?
Welke afwijkingen van de voorspelling zijn te verwachten?
Allemaal vragen waarvan het antwoord in de residuen di
terug is te vinden.
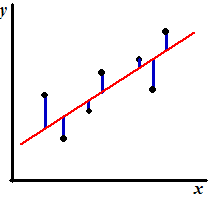
Dat waren die blauwe afwijkinkjes in de figuur hiernaast. Als die groot
zijn, is de voorspelling onnauwkeurig, als ze klein zijn nauwkeurig.
Daarom wordt als maat voor de betrouwbaarheid van de voorspelling de
standaardafwijking van deze residuen genomen. Die geeft immers goed de
spreiding van de residuen aan. |
 |
| |
|
|
fout in voorspelling =
standaardafwijking van de residuen. |
|
| |
|
Die schattingsfout noemen we
σd (de standaardafwijking
van de residuen).
Die is gelukkig erg makkelijk te berekenen:
d = y - (ax + b) = y
- ax -
b dus d + ax + b = y
Om de standaarddeviatie te berekenen moet je de kwadraten van de
afzonderlijke standaarddeviaties optellen:
σd2 +
σax2 +
σb2 =
σy2
Maar omdat a en b constanten zijn is
σax = a◊
σx en is
σb = 0
Dus
σd2
+ a2 ◊ σx2
=
σy2
ofwel
σd2
=
σy2 -
a2 ◊ σx2
Als je dat combineert met de eerder gevonden vergelijking a
= r ◊ σy/σx
dan geeft dat: |
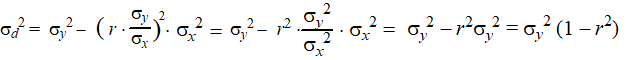 |
| en daaruit volgt dan eenvoudig: |
|
|
|
| |
|
Kortom de gevonden voorspelde
waarde is normaal verdeeld met als gemiddelde de y-waarde
op de regressielijn, en als standaarddeviatie
σd.
(dit alles nog onder de stilzwijgende aannames dat de residuen
"willekeurig" ofwel "normaal verdeeld" zijn, hieronder gaan we
daar dieper op in....).
Als dat zo is, dan kunnen we met de normale verdeling wel weer
uitrekenen hoe groot de kans is dat de werkelijke waarde tussen bepaalde
grenzen zal liggen.
voorbeeld.
Een puntenwolk heeft xgem = 12 met
σx = 4.0 en
ygem = 20 met
σy = 6.2 en r
= 0,8
Hoe groot is de kans dat een nieuw punt in deze wolk met x = 14
een y heeft die groter is dan 24?
a = r ◊ σy/σx = 0.8
◊ 6.2/4.0
= 1,24 en de regressielijn gaat door (12, 20)
dus 20 = 1,24 ◊
12 + b
⇒
b = 5,12.
De regressielijn is y = 1,24x + 5,12
De voorspelling voor x = 14 is dan y = 1,24
◊ 14 + 5,12 = 22,48
Voor de standaarddeviatie geldt
σd
= 6,2 √(1
- 0,82) =
3,72
De kans op meer dan 24 is dan normalcdf(24, ∞
, 22.48, 3.72) = 0,3414 |
| |
|
| |
|
|
OPGAVEN |
| |
|
| 1. |
Neem in de volgende opgave aan
dat toetscijfers continu zijn (dus dat in principe elke waarde
mogelijk is).
In de eerste toetsweek van de examenklassen blijkt er een
duidelijke positieve correlatie te bestaan tussen de behaalde
wiskunde-B cijfers en de wiskunde-D cijfers.
De wiskunde-B cijfers zijn normaal verdeeld met een gemiddelde
van 5,2 en een standaarddeviatie van 1,4.
De wiskunde-D cijfers zijn normaal verdeeld met een gemiddelde
van 6,7 en een standaarddeviatie van 2.1.
Helaas is de wiskunde-D toets van Klazien kwijtgeraakt!!!
Op de wiskunde-B toets had ze een 6.0.
Haar wiskunde leraar stelt voor om haar, volgens de
regressietheorie (met de wiskunde B toets als oorzaak), ongezien een
7,8 te geven.
Daaruit berekent Klazien snel dat de correlatiecoŽfficiŽnt
ongeveer gelijk is geweest aan 0,92. |
| |
|
|
|
| |
a. |
Toon dat aan. |
| |
|
|
| |
b. |
Hoe groot is ongeveer de kans dat
Klazien op de wiskunde D toets een onvoldoende had? |
| |
|
|
|
| 2. |
Men vermoedt dat er een verband is
tussen het geboortegewicht (G in gram) van een baby en de
draagtijd (D in dagen). Een langere draagtijd lijkt een groter
geboortegewicht tot gevolg te hebben. Metingen leverden
onderstaande tabel.
| |
| D |
221 |
224 |
240 |
247 |
250 |
250 |
256 |
267 |
271 |
| G |
1900 |
2650 |
2875 |
2400 |
2140 |
2990 |
3000 |
3100 |
3500 |
|
| |
|
| |
|
|
|
| |
a. |
Geef een vergelijking van de
regressielijn. |
| |
|
|
|
| |
b. |
Neem aan dat de residuen normaal verdeeld zijn.
Stel dat bij mijzelf de draagtijd gelijk was aan 260 dagen. Hoe
groot is dan de kans dat mijn geboortegewicht minder dan 2800
gram was? Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
|
| 3. |
Een groot aantal jaren heeft een
fruitkweker het gemiddelde gewicht van zijn appels en het
gemiddelde aantal uren zonneschijn per dag bijgehouden.
Het gewicht van de appels was normaal verdeeld, met een
gemiddelde van 172 g en een standaarddeviatie van 12 g. Het
aantal uren zon was ook normaal verdeeld, met een gemiddelde van
4,3 uur en een standaarddeviatie van 1,1 uur.
Het blijkt dat er een correlatiecoŽfficiŽnt van 0,86 is. Neem de
uren zon als oorzaak en het gewicht als gevolg,
Hoeveel procent van de appels in een jaar met gemiddeld 4,8 uren
zon zullen een gewicht tussen de 170 en 175 g hebben? |
| |
|
|
|
| |
|
|
|
| 4. |
Bereken voor de onderstaande tabel
de standaarddeviatie van de residuen,
σd,
op twee manieren. |
| |
|
|
|
| |
a. |
Reken alle residuen uit, zet die in
een lijst van je GR en bereken daarna van die lijst de
standaarddeviatie. |
| |
|
|
| |
b. |
Bereken de correlatiecoŽfficiŽnt
r en vervolgens met de formule hierboven de
standaarddeviatie van de residuen. |
| |
|
|
|
| |
| x |
20 |
21 |
22 |
23 |
25 |
26 |
28 |
28 |
30 |
31 |
33 |
33 |
36 |
38 |
| y |
18 |
16 |
18 |
15 |
16 |
14 |
13 |
16 |
14 |
12 |
10 |
14 |
12 |
8 |
|
| |
|
|
r =
-0,874, σy
= 2,752
σd = 1,34 |
|
| |
|
|
|
| 5. |
Bij een groot aantal proefpersonen
is de bloeddruk gemeten en het cafeÔnegebruik. Men vermoedde
namelijk dat een hoge bloeddruk vaak het gevolg is van een hoog
cafeÔnegebruik. Het cafeÔnegebruik (in mg per dag) was normaal
verdeeld met een gemiddelde van 400 en een
standaarddeviatie van 150.
De bloeddrukwaarden (bovendruk in mm Hg) waren ook normaal
verdeeld met een gemiddelde van 122 en een standaarddeviatie van
14.
Voor iemand die 500 mg cafeÔne per dag gebruikt voorspelde men
naar aanleiding van dit onderzoek een bloeddruk van 130 mg
Hg. |
| |
|
|
|
| |
a. |
Hoe groot was de
correlatiecoŽfficiŽnt van dit onderzoek? |
| |
|
|
| |
b. |
Hoe groot is de kans dat deze
persoon een bloeddruk van meer dan 140 zal hebben? |
| |
|
|
|
| |
c. |
Hoe groot zal de kans op een
bloeddruk van meer dan 140 zijn voor iemand die 600 mg
cafeÔne gebruikt? |
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
Scedasticiteit. |
|
| |
|
Ik heb, om eerlijk te zijn, bij
de afleiding van de formule voor
σd
stiekem iets verzwegen......
Het zit hem in die regel waar ik voor de berekening van
s, de kwadraten
optelde:
σd2
+
σax2 +
σb2 =
σy2
Maar dat geldt alleen als de variabelen onafhankelijk van elkaar
zijn!!!!!
Dus dat gaat ervan uit dat
σd
voor elke x hetzelfde is. |
Het gaat er eigenlijk van uit dat de y-waarden bij een bepaalde
x elke keer normaal verdeeld zijn met dezelfde standaarddeviatie.
Zoiets als in de figuur hiernaast.....
Die mini-klokvormpjes geven de verdeling van alle y-waarden bij
een bepaalde x aan. Scedasticiteit betekent "verspreiding"
en we noemen een puntenwolk homoscedastisch als de
spreiding in de y-waarden overal gelijk is (dan hebben alle
klokvormpjes hiernaast dezelfde standaarddeviatie). Als dat niet het
geval is, heet zo'n puntenwolk heteroscedastisch, en in
dat geval mag je de formule voor
σd
hierboven NIET gebruiken! |
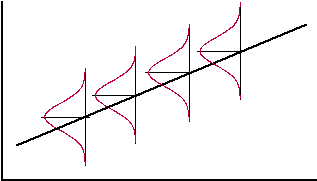 |
| |
|
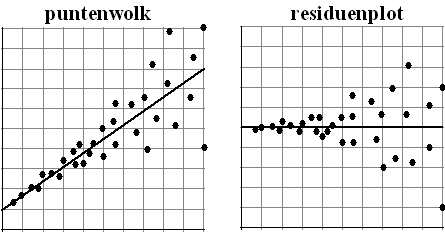
Het komt regelmatig voor dat de
residuen steeds groter worden als x groter worden. Of juist
steeds kleiner. Je ziet dat effect het duidelijkst aan de residuplot.
Als de residuen naar ťťn kant toe steeds groter worden dan is er iets
verdachts aan de hand...
Hieronder zie je zo'n puntenwolk met bijbehorende residuplot. Aan beiden
is eigenlijk wel te zien dat deze puntenwolk heteroscedastisch is. |
| |
|
|
 |
| |
|
| Het waaiert naar rechts toe uit,
dus dat betekent dat
σd
groter wordt als x groter wordt. Hier zul je zeker de
bovenstaande formule voor
σd
niet mogen gebruiken, en kun je daarom weinig zeggen over de
betrouwbaarheid van de voorspelling. |
| |
|
| Normaal
verdeeld? |
| |
|
Als de residuen inderdaad
"willekeurig" zijn, dan zullen ze normaal verdeeld moeten zijn (met
uiteraard gemiddelde
μ = 0). Als dat
niet zo is, dan kun je hun standaarddeviatie
σd
wel uitrekenen, maar daar kun je vervolgens niets mee.
Neem bijvoorbeeld de puntenwolk hieronder. |
| |
|
|
 |
| |
|
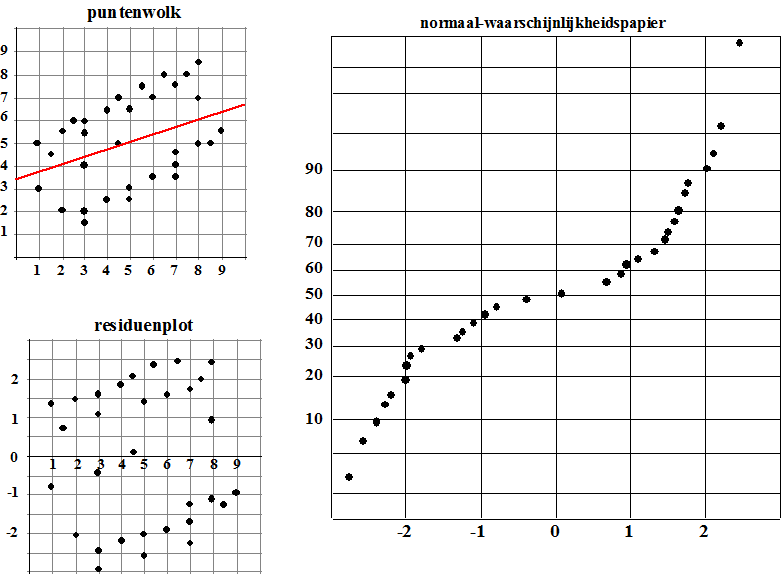
| Linksboven zie je de puntenwolk
met de regressielijn y = 0,35x + 3,33 en correlatiecoŽfficiŽnt
r = 0,4. Linksonder staat de bijbehorende residuplot. Maar
als je die residuen op normaal waarschijnlijkheidspapier tekent, dan
komt daar helemaal geen rechte lijn uit. De residuen zijn dus absoluut
niet normaal verdeeld! Residuen zo rond de 0 komen haast niet voor, en
tussen de 1 en 2,5 en tussen de -1 en -2,5 juist erg vaak. Het lijkt
erop dat we hier te maken hebben met twee aparte populaties |
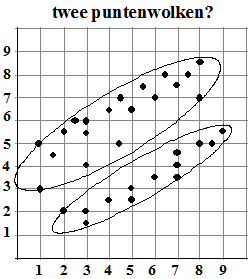
| Als je bijvoorbeeld van de beide "deelpuntenwolken"
hiernaast de correlatiecoŽfficiŽnten uitrekent vind je r = 0,87 voor de
bovenste wolk en voor de onderste r = 0,96.
|
 |
| |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
 |