vectorvoorstelling van een lijn


De vectorvoorstelling van een lijn.	© h.hofstede (h.hofstede@hogeland.nl)

Hoogste tijd om eens op een andere manier tegen een rechte lijn aan te kijken. Dat van die y = ax + b dat weten we nou wel. Er is ook met vectoren een slimme manier om een lijn te beschrijven.
Daarvoor moet je eerst weten wat een plaatsvector is.
Dat is erg makkelijk:

een plaatsvector is een vector met het beginpunt in de oorsprong.

Die mag dus niet meer zomaar overal liggen (zoals een gewone vector) maar moet per se beginnen in de oorsprong. Het nut van een plaatsvector is, dat je de plaats van een punt ermee kunt aangeven.

Terug naar die rechte lijn....
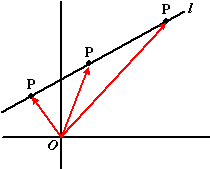
Stel dat je de plaatsvector van een willekeurig punt P van een rechte lijn wilt weten. Die rode hiernaast, maar P kan overal liggen....

Dan moet je als volgt denken:

"Hoe kan ik vanaf de oorsprong elk punt P van de lijn bereiken?"

hmmm....

Stel je voor dat ergens op een snelweg (je weet niet waar) iemand met autopech staat, en je wilt een reparatierobot opdracht geven vanaf de oorsprong naar die pechvogel toe te gaan.

Hoe zou je die robot programmeren?
Hoe bereik je elk punt van de weg?

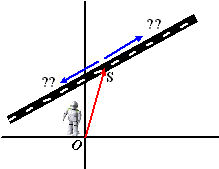
De allersimpelste opdracht die ik kan verzinnen is:
"Loop naar een willekeurig punt van de weg (punt S)".
"Volg de weg beide kanten op totdat je een auto met pech tegenkomt".

Nou, dat is wiskundig geformuleerd eigenlijk het volgende:
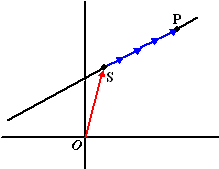
"Neem eerst een plaatsvector naar een willekeurig punt van lijn l (de rode vector hiernaast)"
"Tel daar een willekeurig aantal keer de richting van lijn l (de blauwe vector hiernaast) bij op".
Dan bereik je vanzelf elk punt P van de lijn (dan vind je de plaatsvector van de auto).

In de tekening hiernaast is de blauwe vector vier keer genomen, maar dat aantal hoeft geen geheel getal te zijn, en ook geen positief getal. Alles mag.

Stel bijvoorbeeld dat l de lijn y = 2x + 5 is.
Dan gaat hij bijvoorbeeld door (2, 9) Dus je zou voor S punt (2,9) kunnen kiezen.
l heeft richtingscoëfficiënt 2, dus gaat bij 1 opzij 2 omhoog, dus de vector die de richting van l geeft

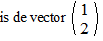Een willekeurig punt van lijn l heeft dan plaatsvector:

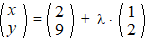Waarbij λ één of ander willekeurig getal is.
Deze manier van een lijn noteren heet een vectorvoorstelling van een lijn.

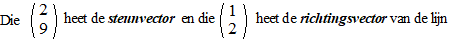Neem je bijvoorbeeld λ = 3 dan kom je in punt (5, 15) en neem je λ = -2 dan kom je in (0, 5); beide zijn inderdaad punten van de lijn.
Andersom kan het ook: wil je in punt (-3, -1) aankomen, dan moet je ervoor zorgen dat de x-coördinaat -3 wordt, dus als je naar de bovenste "regel" van de vectorvoorstelling kijkt zie je dat moet gelden 2 + λ = -3.
Daaruit volgt dat λ = -5. Controle van de y-coördinaat levert met de onderste "regel": y = 9 + 2λ = 9 - 10 = -1, dus dat klopt.

Van de één naar de ander.

We hebben nu twee verschillende manieren om een lijn weer te geven; een vergelijking en een vectorvoorstelling. Het is wel makkelijk als je een beetje handig bent in het omzetten van de één in de ander.

Voorbeeld 1. Geef een vectorvoorstelling van de lijn y = -2x + 8

Kies een willekeurig punt van de lijn, bijvoorbeeld (0, 8) en gebruik de plaatsvector daarvan als steunvector.
De richtingscoëfficiënt is -2, dus bij 1 naar rechts gaat de lijn 2 omlaag, en daarmee is de richtingsvector bekend.

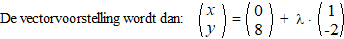Merk op dat er oneindig veel andere mogelijkheden zijn voor de vectorvoorstelling. Als steunvector hadden we elk willekeurig ander punt van de lijn kunnen nemen. En ook de richtingsvector kan best anders: je kunt ook 2 naar rechts en 4 omlaag gaan, of 1 naar links en 2 omhoog, of 4 naar links en 8 omhoog, of..... noem maar op.

Voorbeeld 2.

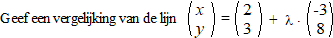De lijn gaat 3 naar links en 8 omhoog, dus de richtingscoëfficiënt is ^Δy/_Δx = ⁸/_-3 = -2²/₃
Dat geeft als vergelijking y = -2²/₃x + b en daar moet het punt (2,3) op liggen
Invullen geeft 3 = -2²/₃ • 2 + b dus b = 8¹/₃.
De vergelijking is dus y = -2²/₃x + 8¹/₃.

Het kan ook nog anders. De bovenste "regel" van de vectorvoorstelling geeft x = 2 - 3l, en de onderste y = 3 + 8l.
Ga nu uit deze twee vergelijkingen λ elimineren (wegwerken)
Maak van de eerste vergelijking λ = .... en vul dat in in de tweede.
Ga zelf maar na dat dat inderdaad ook de eerder gevonden vergelijking van de lijn oplevert.

OPGAVEN

1.	Geef een vectorvoorstelling van de volgende lijnen:

	a.	y = 4x + 3	d.	x = 5

	b.	y = -²/₃x + 5	e.	y = 16 - 2x

	c.	y = -x + 8	f.	y = 10

2.	Geef een vergelijking van de volgende lijnen:

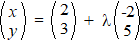
	a.		d.

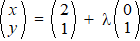
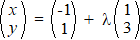
	b.		e.

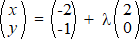
	c.		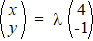f.

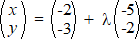3.	Welk van de volgende vectorvoorstellingen stellen dezelfde lijn voor?

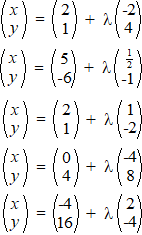
Het snijpunt van twee lijnen.

Als je twee lijnen met een vectorvoorstelling hebt, en je wilt het snijpunt berekenen dan kun je natuurlijk erg conservatief zijn en van beiden eerst een vergelijking maken, en dan van die twee vergelijkingen op de oude vertrouwde manier het snijpunt berekenen. Zeker, dat lukt je vast wel.

Maar waarom niet wat nieuws proberen?

Je kunt van twee vectorvoorstellingen ook het snijpunt berekenen door te bedenken dat die lijnen op dat snijpunt dezelfde x hebben én dezelfde y. Dat betekent dat de bovenste "regel" gelijk moet zijn en ook de onderste "regel". Dat geeft je twee vergelijkingen met twee onbekenden en die zijn makkelijk op te lossen.
(ik hoop dat je snapt dat je bij twee lijnen niet beide letters in de vectorvoorstelling λ kunt noemen. Ze hoeven namelijk niet gelijk te zijn. Meestal noemen we de ene λ en de andere μ)

Voorbeeld 3.

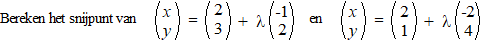De x-vergelijking is 2 - λ = 0 + 3μ en de y-vergelijking is 3 + 2λ = 4 + μ.
Van de eerste kun je maken λ = 2 - 3μ en dat kun je invullen in de tweede.
Dat geeft 3 + 2(2 - 3μ) = 4 + μ ⇒ 7 - 6μ = 4 + μ ⇒ 3 = 7μ ⇒ μ = ³/₇.
Dat geeft het snijpunt x = 3μ = ⁹/₇ en y = 4 + μ = 4³/₇. Het snijpunt is (1²/₇, 4³/₇)

Kan er nog wat misgaan?

Het zou kunnen dat bij dat oplossen zomaar ineens alle letters wegvallen en dat je iets overhoudt als 2 = 2 of 3 = 5 of zo.
Kijk maar:

Voorbeeld 4.

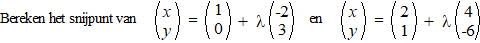De vergelijkingen zijn 1 - 2λ = 2 + 4μ en 3λ = 1 - 6μ.
de eerste geeft λ = -¹/₂ - 2μ en invullen in de tweede levert 3(-¹/₂ - 2μ) = 1 - 6μ
⇒ -1¹/₂ - 6μ = 1 - 6μ ⇒ -1¹/₂ = 1.
Wat is hier aan de hand?
Er is natuurlijk geen enkele l of μ waarvoor geldt dat -1¹/₂ = 1 , dus deze twee lijnen hebben geen snijpunt.
Ze zijn evenwijdig!! Dat kon je al wel zien aan die twee richtingsvectoren natuurlijk.....

En als het oplossen iets zou opleveren wat altijd klopt, zoals 4 = 4 of zo, dan betekent dat voor elke λ en m er een snijpunt is. Dat is alleen maar zo als de twee lijnen samenvallen!

OPGAVEN

Bereken het snijpunt van de volgende lijnen.

(-2, 5)

(6.8, -0.2)

geen

(5¹/₇, 4³/₇)

Bereken het snijpunt van de volgende lijnen.

(-⁹/₁₁, -3⁵/₁₁)

(2, -6)

(³/₇, ¹/₇)