| |
 |
|
Vectoren. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
We gaan het hebben over
verplaatsingen.
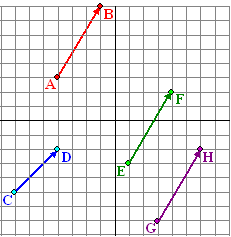
In het vlak hiernaast zou je je van A naar B kunnen verplaatsen, of van
C naar D, of van E naar F, of van G naar H.
Ik hoop dat je ziet dat één van die verplaatsingen anders is dan de
andere drie. Dat zie je het duidelijkst als je pijlen tussen de punten
tekent. Die pijl van C naar D is anders dan de andere drie (andere
richting en andere lengte).
Zo'n verplaatsing (of als je wilt zo'n pijl) heet in de wiskunde een "vector".
Je kunt zo'n vector aangeven door beginpunt en eindpunt te noemen en
daar een pijltje boven te zetten (dat pijltje is nodig omdat je anders
misschien in de war komt met het lijnstuk AB). |
 |
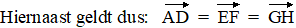 |
| Als je niet alleen
wilt aangeven welke vectoren gelijk zijn, maar ook wilt aangeven hoe
groot zo'n vector nou is, en welke richting hij heeft, |
| dan kun je dat doen
door de verplaatsing in de x-richting en de verplaatsing in de
y-richting te noemen, en die onder elkaar tussen haakjes te zetten.
Dus in dit voorbeeld zó: |
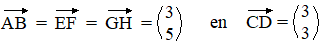 |
Die getallen heten de
kentallen van de vector. Samen leggen ze zo'n vector
helemaal vast. Onthoud goed dat het bovenste kental de verplaatsing in
de x-richting geeft, en het onderste de verplaatsing in de y-richting.
Een negatief kental betekent een verplaatsing naar links/omlaag, dat had
je waarschijnlijk wel geraden.
Zo'n vector is dus bij ons wiskundigen een "pijl" of een "verplaatsing".
Het wordt ook wel een translatie genoemd. Maar eigenlijk
kan het alles zijn wat een grootte en een richting heeft. Natuurkundigen
beschrijven bijvoorbeeld een kracht of een snelheid ook met een vector
(die hebben immers ook een grootte en een richting).
OK. Dat waren een boel afspraken. Even samengevat: |
| |
|
|
|
| • Een vector is een
verplaatsing (een pijl, een translatie). |
| • Een vector heeft een grootte
en een richting. |
| • Je kunt een vector op twee
manieren aangeven: |
| |
 |
|
|
| |
|
|
|
|
Vectoren optellen. |
|
|
| |
|
|
|
Vraag jezelf af hoe
je verplaatsingen zou optellen.
Als je (zie de figuur hiernaast) eerst een verplaatsing zoals van
A naar B zou toepassen en daarna nog een verplaatsing zoals van C naar
D, wat voor totale verplaatsing heb je dan gedaan?
Bedenk goed, dat het alleen maar gaat om de verplaatsing, niet om een
beginpunt of eindpunt. Dat mag alles zijn.
|
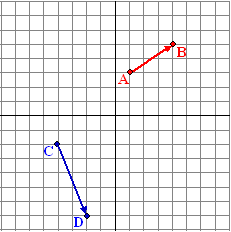 |
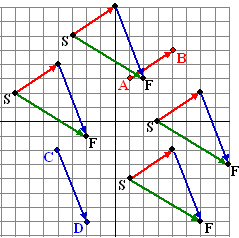
Hiernaast zijn voor
vier verschillen beginpunten S (start) de rode en de blauwe vector na
elkaar toegepast.
Dat levert als totaalverplaatsing de groene vector op, van Start naar
Finish.
Je ziet dat die groene verplaatsing steeds hetzelfde is.
Je krijgt die groene pijl door de rode en de blauwe achter elkaar aan te
leggen, het beginpunt van de blauwe aan het eindpunt van de rode. Dat
noemen we de kop-aan-staart methode.
In de letternotatie zou dat dit opleveren: |
 |
|
|
| Denk erom dat die P
wel dezelfde letter moet zijn, anders liggen de vectoren niet
kop-aan-staart. |
Met kentallen kan het
natuurlijk ook.
De totale x-verplaatsing is hoeveel de eerste vector in de x-richting
verplaatst, plus hoeveel de tweede vector daar nog een bijop doet. En
voor de y-verplaatsing geldt hetzelfde. Ofwel: je mag de
kentallen gewoon bij elkaar optellen. |
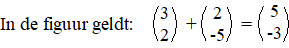 |
| |
|
|
|
| Vectoren optellen: |
| |
|
| 1. |
kop-aan-staart methode |
| 2. |
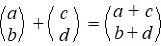
|
|
|
| |
|
|
|
|
Een vector met een getal
vermenigvuldigen. |
| |
|
|
|
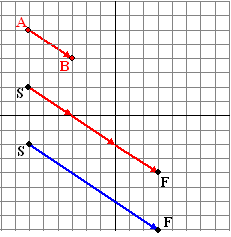
| Ook dat is met
verplaatsingen makkelijk te snappen. Als je de verplaatsing van A naar B
met 3 wilt vermenigvuldigen, dan leg je die pijl gewoon drie keer achter
zichzelf (kop-aan-staart). En met kentallen nog eenvoudiger:
vermenigvuldig beide kentallen met 3. |
 |
| |
|
|
| |
|
| En een vector delen
door een getal gaat heel makkelijk als je je maar bedenkt dat delen door
getal c precies hetzelfde is als vermenigvuldigen met getal
1/c. |
| |
|
|
|
|
Vectoren van elkaar aftrekken. |
| |
|
|
|
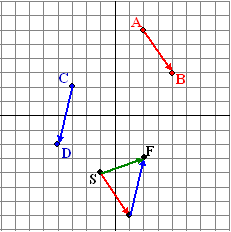
Als je de tweede
verplaatsing niet bij de eerste wilt optellen maar er van aftrekken, dan
moet je dus juist het omgekeerde doen. Ofwel: die tweede pijl moet
je in de andere richting volgen.
Je kunt ook zeggen : je vermenigvuldigt de tweede pijl met -1
(omdraaien) en legt hem dan kop-aan-staart met de eerste. Eigenlijk
hetzelfde als bij getallen: 8 - 3 = 8 + (-3)
|
 |
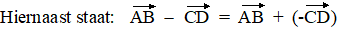 |
| |
|
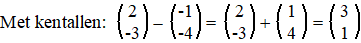 |
| |
|
|
|
|
Vectoren met elkaar
vermenigvuldigen. |
| |
|
|
|
Ik snap dat je daar
erg benieuwd naar bent, maar dat onderwerp moet nog even tot later
wachten.
Sorry, we moeten eerst wat meer over vectoren weten........ |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
|
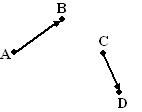
| 1. |
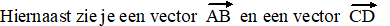 |
 |
| |
Ik heb lekker geen schaalverdeling gegeven, want
je mag geen berekeningen maken.
Teken ergens in deze figuur de volgende vectoren: |
| |
|
|
| |
a. |
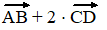 |
| |
|
|
| |
b. |
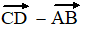 |
| |
|
|
| |
c. |
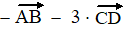 |
| |
|
|
| |
d. |
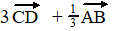 |
| |
|
|
|
|
| 2. |
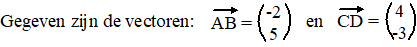 |
| |
Bereken daarmee de kentallen van de
vectoren uit de vorige vraag. |
| |
|
|
|
|
| 3. |
Gegeven zijn het punt P(xp,
yp) en Q(xq, yq)
O is de oorsprong.
Geef de kentallen van de volgende vectoren, uitgedrukt in xp,
yp, xq, yq |
| |
|
|
|
|
| |
a. |
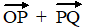 |
|
|
| |
|
|
|
|
| |
b. |
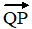 |
|
|
| |
|
|
|
|
| |
c. |
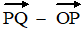 |
|
|
| |
|
|
|
|
| 4. |
Leg uit of de volgende vectoren
evenwijdig zijn of niet: |
| |
|
|
|
|
| |
a. |
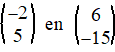 |
|
|
| |
|
|
|
|
| |
b. |
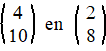 |
|
|
| |
|
|
|
|
| 5. |
Driehoek ABC heeft hoekpunten A(0, 2) en B(3, 6)
en C(10, 0)
P
ligt op zijde AB zodat AP : PB = 2 : 1
Q
ligt op zijde BC zodat BQ : QC = 3 : 1
M is het midden van PQ.
Bereken de lengte van lijnstuk AM. |
| |
|
|
|
|
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|