|
|
 |
|
De uitslag van een figuur. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
 |
| |
|
Een uitslag is in de
wiskunde iets heel anders dan in het dagelijks leven.
De uitslag van een ruimtelijke figuur is eigenlijk niets anders dan een
"bouwplaat zonder plakrandjes" ervan. Als het kan moet je zo'n
uitslag uit één stuk tekenen. Uiteraard zijn er voor één figuur meerdere
mogelijke uitslagen: het hangt er maar vanaf welke ribben je gaat
opensnijden.
Als je het lastig vindt een goede vorm van een uitslag te tekenen,
geef dan de hoekpunten allemaal letters en teken één voor één de
vlakken.
Voorbeeld |
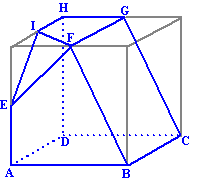
Hiernaast zie je een blauw ruimtelijk figuur in een kubus geplaatst.
De hoekpunten hebben we alvast een letter gegeven.
F, I, E en G zijn middens van de ribben.
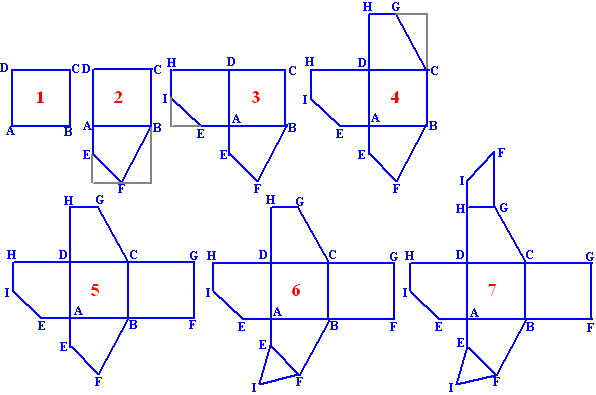
Hieronder zie je in een soort stripje van zeven plaatjes hoe één voor
één alle vlakken in een uitslag zijn getekend. De grijze lijnen
zijn hulplijntjes van de vlakken van de oorspronkelijke kubus. |
 |
| |
|
|
 |
| |
|
|
Op ware grootte. |
| |
|
| Het is natuurlijk wel de bedoeling om zo'n
uitslag op ware grootte te tekenen. Desnoods op schaal, maar ten
opzichte van elkaar moeten de lengtes van alle ribben wel kloppen.
Hoe krijgen we dat voor elkaar?
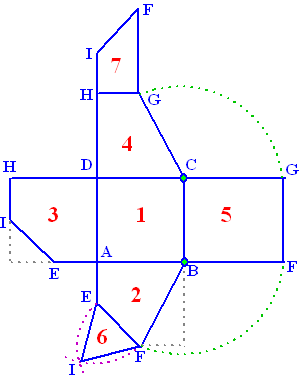
In de einduitslag van het stripverhaal hierboven zie je in de figuur
hiernaast hoe hulplijntjes ervoor gezorgd hebben dat de afmetingen
kloppend werden.
De grijze hulplijntjes bij vlak 2 en 3 waren gewoon afmetingen van de
kubus.
In vlak 5 zijn de lengtes van CG en BF gevonden door de groene cirkels
met die straal en middelpunten C en B te tekenen en die te snijden met
de verlengden van DC en AB. Zo is de lengte automatisch goed.
In vlak 6 is de precieze plaats van punt I gevonden door de paarse
cirkels, beiden met straal EF en met middelpunten E en F met elkaar te
snijden. Driehoek IEF moet immers drie gelijke zijden hebben? |
 |
| |
|
Deze figuur is een mooi voorbeeld
van de drie technieken die we kunnen gebruiken om lijnstukken op ware
grootte te tekenen:
1. Een rechthoekige driehoek gebruiken om schuine lengtes te
construeren (de grijze driehoekjes voor vlak 2 en 3)
2. Getekende lengtes omcirkelen op een andere lijn (de
groene cirkelbogen voor vlak 5).
3. Driehoeken construeren door twee lengtes te omcirkelen (de
paarse cirkelbogen voor vlak 6). |
| |
|
| |
|
| 1. |
Teken een uitslag van de volgende blauwe
ruimtelijke figuren. Ze zijn gemaakt door van een kubus met
ribben 4 cm vlakken af te snijden, waarbij steeds hoekpunten of
middens van ribben zijn gebruikt. |
| |
|
|
|
| |
|
| |
|
|
|
| |
|
|
|
| 2. |
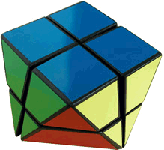
Hiernaast zie je een leuke variant
op de beroemde Rubik's Cube.
Deze figuur heet een "antiprisma".
Het bovenvlak en het ondervlak zijn twee vierkanten die 45º ten
opzichte van elkaar zijn gedraaid. Vervolgens zijn alle
hoekpunten met elkaar verbonden.
Teken een uitslag van zo'n antiprisma als alle ribben even lang
zijn. |
 |
| |
|
|
|
| |
En hiernaast is er nóg
eentje (een zogenaamde "diamond cube").
Teken ook van deze ruimtelijke figuur een uitslag als alle
ribben even lang zijn. |
 |
| |
|
|
|
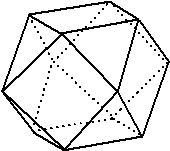
| 3. |
De figuur hiernaast is
ontstaan door van een kubus alle middens van alle ribben met
elkaar te verbinden.
Teken een uitslag. |
 |
| |
|
|
|
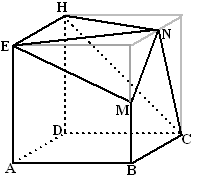
| 4. |
Het lichaam ABCD.EMNH is verkregen door van een kubus met ribben
4 twee piramides af te snijden. Daarbij zijn M en N middens van
ribben.
Teken een uitslag op ware grootte. |
 |
| |
|
|
|
| |
|
|
|
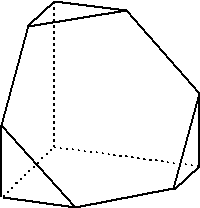
| 5. |
De figuur hiernaast is
ontstaan door van een kubus middens van sommige ribben met
elkaar te verbinden.
Teken een uitslag. |
 |
| |
|
|
|
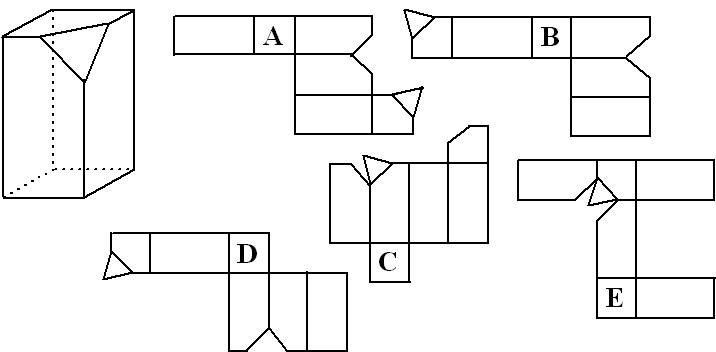
| 6. |
Olympiadevraagstuk.
Hieronder
staat links een ruimtelijke figuur. Het is een balk waarvan in een
hoekpunt een piramide is weggenomen.
rechts staat vijf keer een uitslag getekend.
Welk van de vijf uitslagen hoort bij de balk (er kunnen meerdere goede
antwoorden zijn!) |
| |
|
|
|
| |
 |
| |
|
|
|
 |
|
|
| |
|
| |
|
| De
plaats van de top. |
|
| |
|
Als je een uitslag van een
piramide maakt, dan krijg je steeds één grondvlak. waaraan aan elke
zijde een zijvlak vastzit
Die zijvlakken ontmoeten elkaar uiteraard allemaal in de top. |
Als je een uitslag van een piramide wilt
maken is het handig om te bekijken boven welk punt van het grondvlak die
top nou ligt.
Neem de uitslag hiernaast van een piramide met een vierkant grondvlak.
Om de plaats van de top te vinden draai je de piramide gewoon weer in
elkaar!
|
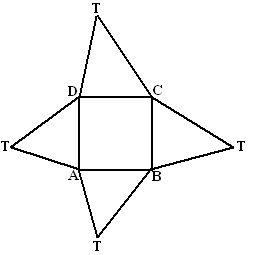 |
Als je bijvoorbeeld het linkervlak TDA
hiernaast weer "omhoog draait" dan blijft de top tijdens dat draaien de
hele tijd boven de rode lijn hiernaast die loodrecht op AD staat.
Dus ergens op die rode lijn ligt het punt waar de top in de ruimtelijke
figuur loodrecht boven ligt
|
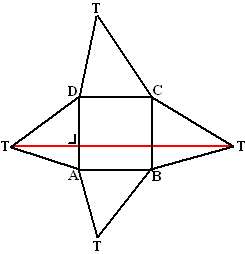 |
Maar volgens die redenering kun je
bijvoorbeeld het achtervlak TDC ook wel weer omhoog draaien, en dan moet
de top boven de blauwe lijn hiernaast liggen (die loodrecht op DC
staat).
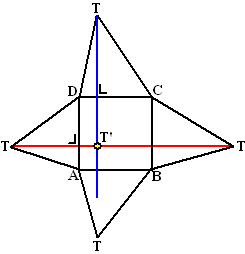
Kortom: de plaats waar de top boven ligt is het snijpunt van de rode en
de blauwe lijn (T' hiernaast). |
 |
|
Eeehhhm... waarom is dit ook alweer handig.....? |
| |
|
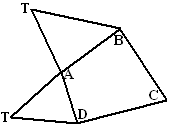
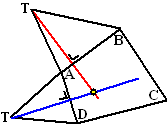
Neem de uitslag van de vierzijdige piramide
met grondvlak ABCD waarvan hiernaast een deel is getekend. Stel dat we
die uitslag af willen maken.
Dan moet daar aan BC en aan DC dus nog een vlak komen.
Maar hoe?.....Om dit op te lossen gaan we eerst de plaats van de
projectie van de top op het grondvlak opsporen. |
 |
Draai vlak TAB weer omhoog dan ligt de top de
hele tijd boven de rode lijn (die loodrecht op AB staat).
Draai valk TAD weer omhoog dan ligt de top de hele tijd boven de blauwe
lijn (die loodrecht op AD staat).
Kortom: het is het snijpunt van beide lijnen!! |
 |
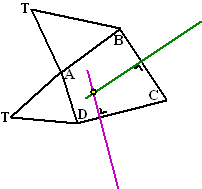
Als je dat eenmaal weet kun je dus vanaf die
T' ook lijnen loodrecht op de andere zijden tekenen. Dat zijn de
groene en de paarse lijn hiernaast.
We weten dus nu dat de top in de uitslag ergens op die groene en die
paarse lijn moet liggen. |
 |
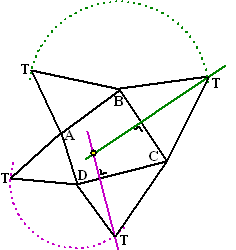
De precieze plaats van die punten T kun je
dan eenvoudig vinden door de lijnen BT en DT om te cirkelen.
Hiernaast zie je hoe dat is gebeurd en hoe dat de volledige uitslag
van de piramide oplevert. |
 |
| |
|
|
|
| |
|
|
De kortste route. |
| |
|
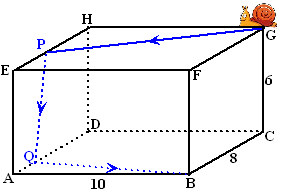
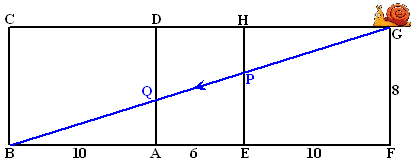
Hiernaast zie je een slak die op
een houten balk (van 6 bij 8 bij 10) in hoekpunt G zit. De slak gaat van G naar B
kruipen over het oppervlak van de balk, maar doet dat via een
punt P op EH en een punt Q op AE. De afmetingen van de balk zijn
hiernaast aangegeven.
Wat is de kortste route die de slak kan volgen?De oplossing
is kinderlijk eenvoudig als je een uitslag van de balk bekijkt
waarin de vlakken EFGH en EHAD en ADBC "aan elkaar" zitten.
Kijk maar:
|
 |
| |
|
|
|
|
 |
| |
|
|
|
De kortste route tussen G en B is nu uiteraard
een rechte lijn.
De lengte vinden we eenvoudig met Pythagoras: BG = √(262 + 82) =
√740
Uit gelijkvormige driehoeken volgt ook vrij eenvoudig de plaats
van de punten P en Q.(AQ = HP = 40/13,
reken dat zelf maar na) |
| |
|
|
|
| |
|
|
|
| 8. |
Bereken bij onderstaande ruimtelijke
figuren de kortste route van P naar Q via de aangegeven
route over het oppervlak van de figuur. |
| |
|
| |
|
| |
|
|
|
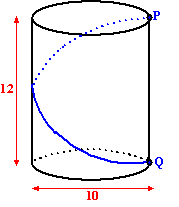
| 9. |
Om een cilinder
met hoogte 12 en diameter 10 wordt een touw gespannen.
Het touw loopt van punt P in het bovenvlak naar punt Q
in het ondervlak, waarbij Q recht onder P ligt.
Het touw wordt strak getrokken waardoor het zo kort
mogelijk is. |
 |
|
|
|
| |
a. |
Wat is het kortste touw dat hiervoor
gebruikt kan worden?
Geef je antwoord in twee decimalen nauwkeurig. |
|
|
|
| |
b. |
Hoe lang is dat touw als het een keer
extra om de cilinder wordt geslagen?
Geef je antwoord in twee decimalen |
| |
|
|
|
| |
|
|
|
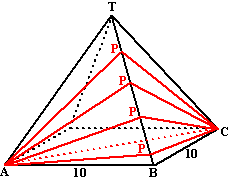
| 10. |
In een
vierzijdige piramide wordt een groot aantal driehoeken
APC getekend, met P ergens op TB.
Het grondvlak van de piramide is 10 bij 10, de hoogte
van de piramide is ook 10.
Welke van deze driehoeken heeft de kleinste omtrek, en
hoe klein is die omtrek? (geef je antwoord in twee
decimalen) |
 |
| |
|
|
| |
|
|
|
| |
|
|
|
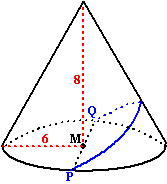
| 11. |
Een kegel heeft
hoogte 8 en straal grondvlak 6.
Van een punt P op de ribbe van het grondvlak wordt over
de kegelmantel een kromme getekend naar punt Q op de
ribbe van het grondvlak, zodat PQ een middellijn van het
grondvlak is.
Wat is de minimale lengte van de getekende kromme? |
 |
| |
|
|
|
|
 |
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
 |
| |
|
|
|
| |
|
|
|
|
| |
|