De stelling van Thales

© h.hofstede (h.hofstede@hogeland.nl)

       
Deze stelling is een heel eenvoudig gevolg (eigenlijk een speciaal geval) van de stelling van de vorige les.
Daarom herhaal ik die nog maar even:
       

De middelpuntshoek van een koorde is dubbel zo groot als de omtrekshoek ervan.

       
Maar wat gebeurt er als die koorde door het middelpunt van die cirkel gaat?

JUIST!

Dan is de middelpuntshoek gelijk aan 180º, immers je gaat van de ene kant van de cirkel helemaal naar de andere.
Maar dat betekent dat de omtrekshoek van een middellijn gelijk moet zijn aan de helft daarvan, dus aan 90º

Middellijnen maken met punten op de omtrek rechte hoeken!
       
Hou vooral het plaatje hiernaast in gedachten!
Al die gele stippen zijn rechte hoeken.


Je zult dit plaatje nog vaak tegenkomen!!!

       

Als P op een cirkel ligt waarvan AB een middellijn is, dan is ∠APB = 90º

       
Er is nog een tweede, erg eenvoudige manier om het bewijs hiervan in te zien.

Omdat MA en MP en MB allemaal gelijk zijn aan de straal van de cirkel, zijn de driehoeken MAP en MBP gelijkbenig.
Dat betekent dat de basishoeken gelijk zijn. In de figuur hiernaast twee gelijke rode en twee gelijke groene hoeken.
Omdat de hoeken van een driehoek samen 180º zijn, zijn twee rode plus twee groene hoeken samen 180º.
Dus één rode en één groene hoek zijn samen 90º
Dus ∠APB = 90º
q.e.d.

       
De stelling van Thales.
       
Je mag de eigenschap van die rechte hoek ook omkeren. Als je dat doet krijg je de stelling van Thales:
       

Als ABC een rechte hoek C heeft, dan is er een cirkel door A, B en C  waarvan AB de middellijn is. 

       
Deze cirkel heet de omgeschreven cirkel van driehoek ABC.
Ook Euclides beschrijft deze stelling, namelijk in  propositie  III.31.
Je zou de eerste stelling van deze les dus heel goed de omgekeerde stelling van Thales kunnen noemen.....
       
       
OPGAVEN
       
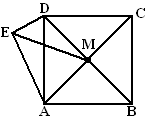
1. Op de zijde van een vierkant ABCD wordt een rechthoekige driehoek AED getekend, waarvan hoek E de rechte hoek is.
M is het middelpunt van het vierkant.
Lijn EM verdeelt de hoek DEA in twee gelijke hoeken.

Toon dat aan.

     
 
hint: Toon aan dat MADE op één cirkel liggen.
       
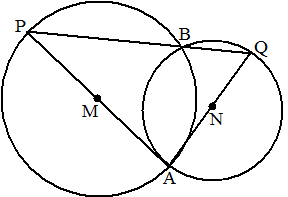
2. Twee cirkels snijden elkaar in A en B.
M en N zijn de middelpunten van die cirkels.
AM en AN snijden de cirkels in P en Q

Toon aan dat B op lijnstuk PQ ligt.
       
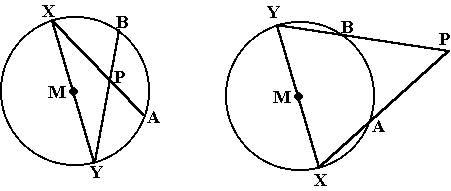
3. A en B zijn twee vaste punten op een cirkel (zodat AB géén middellijn is)
XMY is een willekeurige middellijn van de cirkel.
P is het snijpunt van AX en BY.
Er zijn meerdere mogelijkheden voor de plaats van punt P, zoals je in de figuren hieronder ziet.
       
 

       
  a. Toon aan dat ∠XBY een rechte hoek is.
       
  b. Toon aan dat ∠AXB een constante hoek is, onafhankelijk van de plaats van X.
       
  c. Toon aan dat ∠APB een constante hoek is.
       
  d. Wat zegt dat over de plaats van punt P?  
       
4. Examenvraagstuk VWO Wiskunde B, 2011.

Gegeven is een cirkel met middelpunt M.
Punt C ligt binnen de cirkel. C is niet gelijk aan M.
PQ is een koorde door C die niet door M gaat. Het midden van PQ is S.

Bewijs dat S op de cirkel met middellijn MC ligt.
       
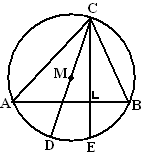
5. Gegeven is een driehoek ABC met omgeschreven cirkel met middelpunt M. CM snijdt de cirkel in D
Hoogtelijn CF snijdt de cirkel in E.

Het blijkt dat AD = BE.

     
  a. Toon dat aan.
     
  b. Toon aan dat DE en AB evenwijdig zijn.
       
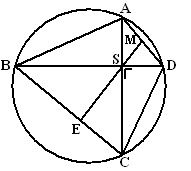
6. ABCD liggen op een cirkel zodat AC en BD loodrecht op elkaar staan.
M is het midden van AD.
S is het snijpunt van AC en BD.
MS snijdt BC in punt E.

     
  Toon aan dat  ∠MDS = ∠BSE
     
     
       
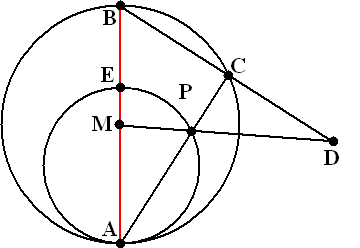
7. In een cirkel met middelpunt M wordt diameter AB getekend. E is een punt op AB zodat BE = 1/3•AB.
Teken de cirkel waarvan AE een diameter is.
Kies een willekeurig punt P op de tweede cirkel. 
C is het snijpunt van AP met de eerste cirkel.
BC en MP snijden elkaar in D.

Bewijs dat C dan het midden van BD is.
   
hint: ΔMEP is gelijkvormig met ΔMBD.
       
 

       
8.

     
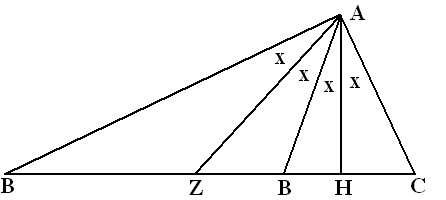
  Hoek A van een driehoek wordt door de hoogtelijn, de zwaartelijn, en de bissectrice vanuit A in vier gelijke delen verdeeld. Hoeveel graden is hoek A? 
       
 
HINT: Teken de omgeschreven cirkel van de driehoek
en trek de lijnen door

90º
       
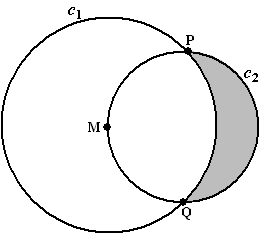
9. Cirkel c1 met middelpunt M verdeelt de omtrek van cirkel c2 in twee gelijke stukken.
M ligt op cirkel c2
De oppervlakte van c2 is gelijk aan p.

Bereken de oppervlakte van het grijze deel in de figuur. 

 
   

1
       
10. Een middellijn van een cirkel wordt in vier gelijk stukken verdeeld.
De punten A en B worden gebruikt als hoekpunten van een driehoek.
Het derde hoekpunt P wordt willekeurig ergens binnen de halve cirkel gekozen.

Hoe groot is de kans dat de hoek P stomp is?

     

25%
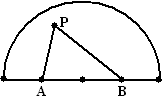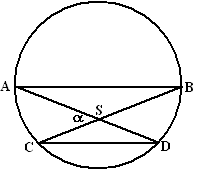
11. AB is middellijn van een cirkel.
De figuur hiernaast is symmetrisch.

De verhouding van de oppervlakten van de driehoeken CSD en ASB is gelijk aan sin2α.

Toon dat aan.

       
 
     

© h.hofstede (h.hofstede@hogeland.nl)