groepentheorie: D4


De symmetrieën van een vierkant	© h.hofstede (h.hofstede@hogeland.nl)

De allereerste vraag daarbij is "Hoeveel symmetrieën zijn er eigenlijk?"
Dat kun je ontdekken door naar de hoekpunten te kijken. Noem de hoekpunten ABCD, dan zijn er 4! = 24 mogelijke volgorden van die hoekpunten (aantal permutaties, weet je nog?). Betekent dat dat er dan ook 24 symmetrieën zijn?

Gelukkig niet.

Het zit hem erin dat de afstanden AC en BD (de diagonalen) langer zijn dan de zijden. Als bij de beeldfiguur de afstanden gelijk moeten blijven, dan mogen dus A en C en ook B en D niet naast elkaar komen te liggen.

ABCD   BACD   CABD   DABC
ABDC BADC CADB DACB
ACBD   BCAD   CBAD   DBAC
ACDB BCDA   CBDA   DBCA
ADBC BDAC   CDAB   DCAB
ADCB BDCA   CDBA DCBA

Van de 24 permutaties blijven er nog maar 8 over.
Dat zijn:

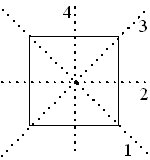
• de identiteit I
• spiegelen in de lijnen 1, 2, 3, 4
• draaien over 90º, 180º, 270º

(Die symmetrieën had je natuurlijk ook wel meteen uit de tekening van het vierkant kunnen halen, maar ik wou even laten zien dat het aantal elementen vaak te maken heeft met permutaties; verderop daarover meer).

De 8 symmetrieeën van het vierkant vormen groep D₄.

Ook hier is natuurlijk weer zo'n "na-elkaar-uitvoeren" tabel voor te maken.

Die zie je hiernaast
Denk eraan: de bewerking in de kolom (vooraan) komt na de bewerking in de rij (bovenaan). Waarom dat van belang is? Nou, zoals je aan de tabel wel ziet geldt in deze groep de commutatieve eigenschap NIET! De tabel is niet symmetrisch ten opzichte van de hoofddiagonaal.
Zo is bijvoorbeeld S₁ o S₂ = R₂₇₀ en S₂ o S₁ = R₉₀.

Verder staat er op de hoofddiagonaal niet meer elke keer de I. Bij R₉₀ en R₂₇₀ niet. Dat betekent dat die niet orde 2 hebben. Ga zelf maar na dat ze zelfs orde 4 hebben.

Er is nog iets interessants met deze groep aan de hand. Bekijk bijvoorbeeld alleen de draaiing over 90º, R₉₀, en de spiegeling in de x-as (S₂)

o	I	S₁	S₂	S₃	S₄	R₉₀	R₁₈₀	R₂₇₀
I	I	S₁	S₂	S₃	S₄	R₉₀	R₁₈₀	R₂₇₀
S₁	S₁	I	R₂₇₀	R₁₈₀	R₉₀	S₄	S₃	S₂
S₂	S₂	R₉₀	I	R₂₇₀	R₁₈₀	S₁	S₄	S₃
S₃	S₃	R₁₈₀	R₉₀	I	R₂₇₀	S₂	S₁	S₄
S₄	S₄	R₂₇₀	R₁₈₀	R₉₀	I	S₃	S₂	S₁
R₉₀	R₉₀	S₂	S₃	S₄	S₁	R₁₈₀	R₂₇₀	I
R₁₈₀	R₁₈₀	S₃	S₄	S₁	S₂	R₂₇₀	I	R₉₀
R₂₇₀	R₂₇₀	S₄	S₁	S₂	S₃	I	R₉₀	R₁₈₀

Als je die herhaaldelijk gaat toepassen, krijg je alle andere symmetrieën, kijk maar:

R₉₀ o S₂ = S₃,
R₉₀ o S₃ = R₉₀o (R₉₀ o S₂) = S₄,
R₉₀ o S₄ = (R₉₀ o (R₉₀ o (R₉₀ o S₂) = S₁
S₂ o S₂ = I
R₉₀ o R₉₀ = R₁₈₀
R₁₈₀ o R₉₀ = (R₉₀ o R₉₀) o R₉₀ = R₂₇₀

En zo hebben we al de andere symmetrieën samengesteld uit alleen maar S₂ en R₉₀. We zeggen daarom dat D₄ wordt voortgebracht door S₂ en R₉₀.

D₄ wordt voortgebracht door S₂ en R₉₀

1.	Door welke andere combinaties van twee symmetrieën wordt D₄ nog meer voortgebracht?

Maar omdat dat zo is, kun je elke symmetrie uit de verzameling D₄ ook wel schrijven als R₉₀ⁱ o S₂^j (een aantal maal R₉₀ en S₂ na elkaar). Noem die twee basissymmetrieën even R en S (dus laat de ₉₀ en ₂ uit luiheid even weg), dan is elke symmetrie dus te schrijven als Rⁱ o S^j . En die zijn razendsnel met elkaar te vermenigvuldigen.
Kijk maar:

•

R^a o R^b = R^{a + b} waarbij a + b modulo 4 gerekend mogen worden.
Klopt natuurlijk: als je eerst b keer over 90º draait en daarna nog a keer, dan draai je in totaal a + b keer over 90º, en dat mag modulo 4, immers elke vier keer over 90º draaien levert niets op.

•

S^a o S^b = S^{a + b} waarbij a + b modulo 2 gerekend mogen worden.
Klopt natuurlijk: elke twee keer spiegelen in dezelfde lijn levert samen niets op.

En ook als de S en R in een andere volgorde staan kun je ze snel verwisselen:
Omdat R^a o S een spiegeling is (kijk maar in de tabel), is de orde ervan 2, dus geldt (R^a o S) o (R^a o S) = I

Pas nu beide kanten R^-a toe: R^-a o (R^a o S) o (R^a o S) = S o (R^a o S) = R^-ao I = R^-a
(Daar aan de linkerkant hebben de R^-a en R^a elkaar opgeheven).

Pas nu beide kanten nog een keer S toe: S o (S o (R^a o S)) = R^a o S = S o R^-a
(Daar aan de linkerkant hebben nu S en S elkaar opgeheven).
Dat geeft de verwisselregel:

R^a o S = S o R^-a

Voorbeeld: bereken R² o S o R o S o R^-3 o R o S
R² o S o R o S o (R^-3 o R) o S = R² o S o R o S o R^-2 o S   (R samennemen)
R² o S o R o (S o R^-2) o S = R² o S o R o (R²o S) o S   (verwisselregel)
R² o S o (R o R²) o (S o S) = R² o S o R³   (R en S samennemen)
R² o S o R³ = R² o R^-3 o S   (verwisselregel)
R^-1 o S
R³ o S

Permutaties en Cykelnotatie.

We zagen hierboven al hoe je ook de 8 symmetrieën van het vierkant als een permutatie kunt opschrijven. Je kijkt gewoon welk hoekpunt wáár terechtkomt. Dat gaf deze 8 mogelijkheden:
ABCD, ADCB, BADC, BCDA, CBAD, CDAB, DABC, DCBA.

Door alleen aan te geven welke hoekpunten veranderen, en waar die terechtkomen kan het nog effectiever genoteerd worden. Neem bijvoorbeeld ADCB. Daarin zijn A en C op hun plaats gebleven, en B en D verwisseld.
Dat geven we aan met (BD) en dat betekent: B gaat naar D en D gaat naar B. Degenen die niet genoemd worden blijven automatisch op hun plaats. Dat tussen haakjes heet een cykel. Vrij vertaald een "kringetje"; het geeft inderdaad aan hoe de punten in een kringetje achter elkaar aan draaien. Dus (BAC) zou betekenen: B gaat naar A, A gaat naar C en C gaat naar B (de laatste begint weer vooraan).

Dus (ADC) zou betekenen: A gaat naar D, D gaat naar C en C gaat naar A, en B blijft op zijn plaats.
Dus (AD)(BC) zou betekenen: A gaat naar D en D gaat naar A, en B gaat naar C en C gaat naar B.

Deze laatste twee zijn uiteraard geen symmetrieën van het vierkant.....Dat had je hopelijk al wel gezien....

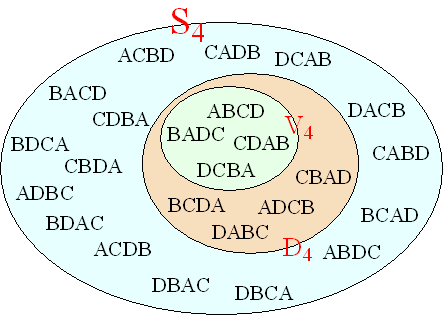
Hieronder zie je de verzameling van alle mogelijke permutaties van 4 hoekpunten (S₄), met daarin de deelverzamelingen V₄ en D₄ zie we tot nu toe al vonden aangegeven.

Je ziet dat V₄ een deelverzameling van D₄ is, en D₄ weer van S₄.
De elementen R en S die we hierboven gebruikten om de hele D₄ voort te brengen zou je kunnen aan geven als R = (BCDA) en S = (DCBA)

Een eigenschap van S4.

De hele verzameling S₄ (alle permutaties) heeft ook een aardige eigenschap, en dat is, dat hij helemaal wordt voortgebracht door de transposities. Een transpositie is een verwisseling van twee hoekpunten met elkaar. Het blijkt dus dat je door alleen maar verwisselingen toe te passen elke permutatie kunt "maken".
Het bewijs daarvan is een sterk staaltje van volledige inductie, en moet je hiernaast maar lezen als het je interesseert.

S₄ wordt voortgebracht door transposities.

Kunnen we ons iets voorstellen bij de hele groep S₄?
Jazeker.
Als alle 24 permutaties mogelijk moeten zijn, dan moeten dus alle afstanden van de punten A, B, C en D gelijk zijn.
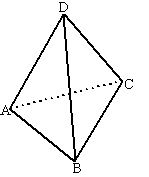
Dat kan bijvoorbeeld door de symmetrieën van het regelmatige viervlak hiernaast te bekijken.

Dan kun je nu eenvoudig aantonen door de stelling over de transposities hierboven te gebruiken. Een transpositie (verwisseling van twee hoekpunten) is van het viervlak altijd een symmetrie. Kijk bijvoorbeeld naar de transpositie (AB). Dat is hetzelfde als de figuur spiegelen in het middelloodvlak van AB (dat door C en D gaat)

Zo kun je elke transpositie als een spiegeling in een middelloodvlak voorstellen. Dus elke transpositie is een symmetrie, dus alle 24 elementen van S₄ zijn te maken (want die zijn allemaal te maken uit de transposities zei onze stelling immers....? toch........??).