| 1. |
Bereken van bovenstaand voorbeeld (gemiddeld
aantal ogen van een dobbelsteen) de standaarddeviatie bij 1 keer
gooien, bij 10 keer gooien en bij 100 keer gooien. |
| |
|
|
|
| |
|
|
|
| 2. |
Als je met een muntstuk gooit en het aantal keer
"KOP" telt, dan zal dat gemiddeld natuurlijk gelijk zijn aan
0,5. |
| |
|
|
|
| |
a. |
Hoe groot is de standaarddeviatie
van dat gemiddelde als je 20 keer gooit? |
| |
|
|
|
| |
b. |
Hoe vaak moet je gooien zodat de
standaarddeviatie minder dan 0,01 is? |
| |
|
|
|
| |
|
|
|
| 3. |
Van alle autorijders 's nachts heeft
5% een te hoog alcoholpromillage. Verder is bekend dat van 12%
van de autorijders de papieren niet in orde zijn.
De eerste overtreding geeft een boete van €120,- en de
tweede een boete van €80,-
Natuurlijk zijn er ook automobilisten die beide bekeuringen
krijgen!
Neem aan dat er geen verband tussen beide overtredingen is.
Op een nacht controleert de politie 140 auto's. |
| |
|
|
|
| |
a. |
Leg uit waarom de gemiddelde boete
per automobilist gelijk is aan €15,60 |
| |
|
|
|
| |
b. |
Bereken de standaarddeviatie van dit
bedrag. |
| |
|
|
|
| |
|
|
|
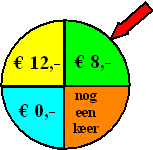
| 4. |
Bij een kermisattractie
mag je de schijf hiernaast draaien en krijg je het bedrag dat
bij de pijl verschijnt. Als de pijl in het oranje gebied staat
mag je nog een keer draaien. Dat geldt maar één keer, dus daarna
wéér oranje levert niets meer op.
Om te mogen spelen moet je €6,50 betalen. |
 |
| |
|
|
| |
a. |
Hoe groot is de gemiddelde winst
die de exploitant per spel verwacht te krijgen? |
| |
|
|
| |
b. |
Hoe groot is de standaarddeviatie
van die gemiddelde winst per spel? |
| |
|
|
| |
c. |
Hoeveel mensen moeten er op een avond meespelen
zodat de standaarddeviatie van de winst van de exploitant
kleiner is dan de verwachte winst zélf? |
|
| |
|
|
| |
|
|
|
| 5. |
In een vaas zitten 16 rode en 9
witte knikkers. Iemand haalt er elke ochtend, zonder
terugleggen, twee willekeurige knikkers uit, kijkt hoeveel roden
daarbij zijn, en legt ze weer terug. |
| |
|
|
|
| |
a. |
Bereken de verwachtingswaarde en de
standaarddeviatie van het aantal rode knikkers dat op een dag
gepakt wordt. |
| |
|
|
|
| |
b. |
Bereken de verwachtingswaarde en de
standaarddeviatie van het gemiddeld aantal rode knikkers per dag
dat over in periode van 20 dagen gepakt wordt. |
| |
|
|
|
| |
|
|
 |