| |
 |
| |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| De
Som- en Productmethode |
|
|
| Laten we van een aantal
kwadratische vergelijkingen de haakjes wegwerken: |
|
|
(x - 3)(x
- 4) =
(x + 2)(x
- 5)
=
(x + 6)(x + 12)
= |
x2
- 4x - 3x
+ 12
x2 + 2x - 5x
- 10
x2 + 6x + 12x + 72 |
= x2
- 7x
+ 12
= x2 - 3x
- 10
= x2 + 18x
+ 72 |
|
|
|
Daar staat eigenlijk
steeds (x + a)(x + b) = x2
+ ....x + ......
-3 en -4
leveren -7 en 12
2 en -5
leveren -3 en -10
6 en 12
leveren 18 en 72
Zoals je ziet, is: laatste getal
= a • b
en het middelste getal
= a + b
En nu komt de vraag van deze les: |
|
|
|
Kunnen we het
ook andersom? |
|
|
Ofwel: als we een kwadratische
formule zonder haakjes krijgen kunnen we dan die haakjes er weer in
zetten?
Voorbeeld: x2 + 7x
+ 12 = (x + ?
)(x + ? )
We zoeken dus twee getallen a
en b zodat geldt a
• b = 12
en a + b = 7.
een beetje proberen levert al gauw a
= 3 en b = 4 (of
andersom) |
|
|
| 1 |
Schrijf de volgende formules in de
vorm (x + a)(x + b) |
| |
|
|
|
|
|
|
|
a. |
x2 + 5x + 6 |
|
f. |
x2 + 19x + 60 |
|
|
b. |
x2 + 9x + 14 |
|
g. |
x2 + 8x + 16 |
|
|
c. |
x2 - 6x
- 16 |
|
h. |
x2 - 20x + 64 |
|
|
d. |
x2 - 10x + 21 |
|
i. |
x2 + 7x
- 18 |
|
|
e. |
x2 + 12x
- 28 |
|
j. |
x2 + 3x
- 40 |
|
|
|
|
| 2. |
Schrijf de volgende formules in de
vorm (x + a)(x + b) |
| |
|
|
|
|
|
|
|
a. |
-12 + x2 + 4x |
|
c. |
x2 + 45 + 18x |
|
|
b. |
5x - 14 + x2 |
|
d. |
6x - 7 + x2 |
|
|
|
|
|
|
| Handige tip |
|
Als je het
moeilijk vindt om die twee getallen te vinden, kijk dan eerst naar het
getal zonder x erbij.
Dat moet gelijk zijn aan a • b en daar zijn vaak
niet zoveel mogelijkheden voor.
Neem die laatste van vraag 1: x2 + 3x
- 40.
Als je 40 ziet, dan zijn eigenlijk de enige mogelijkheden: 40 •
1 en 20 • 2 en 10 • 4 en 8 •
5 en dat was het.
Vraag je daarna af: met welk van deze koppels kan ik het getal 3
fabriceren met plus of min?
Dan kom je al gauw uit op 8 - 5, en daarmee heb je het antwoord
gevonden. |
|
| Wat te doen
als er voor het kwadraat nog een getal staat? |
|
|
Op de eerste plaats: Niet
in paniek raken. Het is maar een getal....
Zet dat getal eerst buiten haakjes, en pas dan bovenstaande methode toe
op het deel binnen de haakjes.
Voorbeeld:
3x2 + 6x - 72 = 3(x2
+ 2x - 24) = 3(x + 6)(x
- 4).
Voorbeeld:
8 - x2 - 2x = -x2
- 2x
+ 8 = -(x2 + 2x - 8) = -(x
- 2)(x
+ 4) |
|
|
| 3. |
Ontbind in factoren: |
| |
|
|
|
|
|
|
|
a. |
2x2 + 4x
- 6 |
|
d. |
6x2 - 24x + 24 |
|
|
b. |
0,5x2 - 5x + 8 |
|
e. |
-x2 + 6x
- 5 |
|
|
c. |
3x2 - 9x + 6 |
|
f. |
-4x2 - 32x
- 28 |
|
|
|
| Maar wat
hebben we eigenlijk aan al deze flauwekul? |
|
|
| Het nut ervan zit hem in de
volgende eenvoudige constatering: |
|
|
|
|
Als voor twee getallen A en B geldt A
• B = 0
Dan is A = 0 óf B = 0 |
|
|
|
Als we willen oplossen x2
+ 13x + 42 = 0 dan is dat niet zo makkelijk.
Maar als we het schrijven als (x + 6)(x + 7) = 0 dan
wel!!!
Immers daar staat A • B = 0 tenminste als je neemt A = x + 6
en B = x + 7
A = 0 geeft x = -6
B = 0 geeft x = -7
De oplossingen van x2 + 13x + 42 = 0 zijn
daarom x = -6 en x = -7 |
|
|
| 4. |
Los op: |
|
| |
|
|
|
|
|
| a. |
x2 + 6x
- 16 = 0 |
|
e. |
x2 + 5x = 14 |
|
| b. |
x2 + 5x
- 6 = 0 |
|
f. |
2x2 + 18x + 16 = 0 |
|
| c. |
x2 + 9x + 20 = 0 |
|
g. |
x2 = 4x + 21 |
|
| d. |
x2 - 8x + 15 = 0 |
|
h. |
x2 + 4x = 5x
+ 30 |
|
|
|
|
|
|
|
|
| 5. |
| a. |
Bereken algebraïsch de coördinaten van de
snijpunten van y = 2x + 4 en y
= x2 + 6x - 1 |
| |
|
| b. |
Een lijn op hoogte y = 10 snijdt de
parabool y = x2 + 2x
- 5 in de
punten A en B.
Bereken de afstand AB. |
| |
|
| c. |
Bereken algebraïsch de snijpunten van de
parabolen y = x2 + 2x
-
1 en y = 2x2
- 5x +
9 |
| |
|
|
|
|
| 6. |
| Los op: |
| |
|
|
|
|
|
| a. |
(2x + 8)(5 - 4x) = 0 |
|
e. |
(x + 5)(x - 3) = 4x |
|
| b. |
(x + 2)(x - 4) = 16 |
|
f. |
x2 (6x
- 4) = 0 |
|
| c. |
(4 - 6x)(x + 2) = 0 |
|
g. |
(4x + 5)2 = 0 |
|
| d. |
(x2 - 4)(2x + 5) = 0 |
|
h. |
(3x + 6)(2x - 7)(x + 4) = 0 |
|
|
|
|
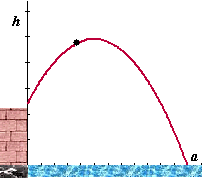
| 7. |
Iemand gooit een steen
met een boog vanaf een muur in een rivier. De steen volgt een
mooie paraboolbaan waarvoor de formule h(t)
= -0,1a2 + a + 2,4 geldt.
Daarin is h de hoogte boven het wateroppervlak en a
de horizontale afstand vanaf de plaats van weggooien (h
en a in meters). |
|
|
|
| |
|
| a. |
Hoe hoog boven het water laat de
werper de steen los? |
| |
|
| b. |
Hoe ver vanaf de muur komt de steen
in het water terecht? |
| |
|
| c. |
Wat is de grootste hoogte die de steen
bereikt? |
| |
|
|
|
|
|
|
| |
|
| 8. |
Ruim 1000 jaar geleden schreef de beroemde Arabische
wiskundige Al-Kwarizmi het volgende probleem op: |
|
|
|
| Op een vierkant staan twee
rechthoeken, elk met een lengte van 5 eenheden. Samengenomen is
de oppervlakte 39 eenheden. Hoeveel eenheden is de zijde van het
vierkant? |
|
| |
|
| |
|
| 9. |
Het fotolijstje
hiernaast heeft een rand die overal even breed is. De buitenafmetingen
van het lijstje zijn 30 bij 40 cm.
De oppervlakte van de foto blijkt even groot te zijn als de oppervlakte
van de rand.
Bereken de breedte van de rand. |
 |
| |
|
| |
|
|
| 10. |
Als f(x) = x2
- 7x + k en f(k) = -9
bereken dan f(-1) |
| |
|
|
|
11. |
Vijf opeenvolgende positieve getallen worden gekwadrateerd en die
kwadraten worden opgeteld.
Dat geeft als antwoord 3135.
Wat waren de getallen? |
|
|
|
|
|
|
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|
| |
|
|
|