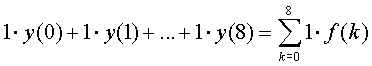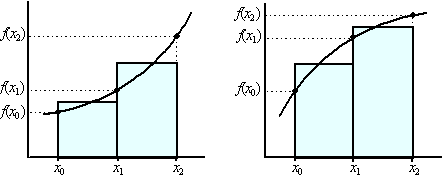© h.hofstede (h.hofstede@hogeland.nl)
De oppervlakte onder een grafiek.
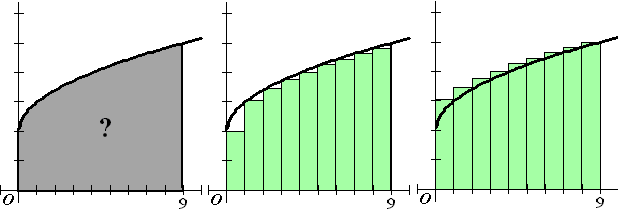
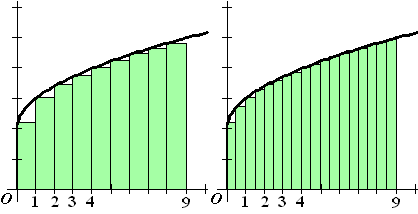
Stel dat we graag de oppervlakte tussen x = 0 en x = 9 onder de grafiek van de functie f(x)  = 2 + √x willen bepalen.
Dat is de grijze oppervlakte hieronder.

In de tweede figuur wordt deze oppervlakte benaderd door negen groene rechthoekjes. De werkelijke oppervlakte is natuurlijk groter, want we zien daar boven tegen de grafiek aan een aantal "gaatjes", maar als we deze negen rechthoekjes uitrekenen hebben we al wel een aardig idee van de juiste oppervlakte. Een soort van schatting dus.
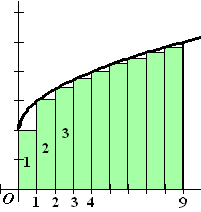
De hoogte van een rechthoekje is steeds te berekenen doordat het de y is die bij de x van de linkerkant hoort:
 
rechthoekje 1 heeft hoogte  f(0) = 2 + √0
rechthoekje 2 heeft hoogte  f(1) = 2 + √1
rechthoekje 3 heeft hoogte  f(2) = 2 + √2
....

De breedte van de rechthoekjes is steeds 1, dus de totale oppervlakte wordt:


Daar komt uit  2 + (2 + √1) + (2 + √2) + ... + (2 + √8) ≈ 34,306
Op je TI-83 gaat dat het snelst zó:
STAT - EDIT
in L1 zet je de getallen 0, 1, 2, 3, 4, 5, 6, 7, 8
ga op de naam L2 staan en druk op ENTER, dan kom je onder in beeld.
voer in L2 = 2 + √(L1)
2nd - QUIT en dan  2nd - LIST - MATH - sum(L2)  geeft het antwoord

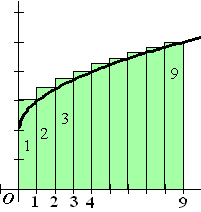
Maar natuurlijk is dit antwoord te laag. Je ziet aan de figuur direct dat er allemaal kleine stukjes missen. De 34,306 geeft dus een ondergrens voor de werkelijke oppervlakte aan, en heet daarom ook een ONDERSOM.

In de figuur hiernaast is dat net andersom......

rechthoekje 1 heeft hoogte  f(1) = 2 + √1
rechthoekje 2 heeft hoogte f (2) = 2 + √2
...
Op deze manier wordt de totale oppervlakte: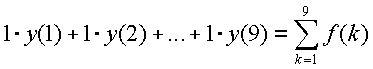

Daar komt uit 37,306 en aan de figuur zie je direct dat dit een BOVENSOM is; de werkelijke oppervlakte zal kleiner zijn.
de voorlopige conclusie is:  

34,306 < Oppervlakte < 37,306
Deze beide sommen heten Riemann-sommen, genoemd naar de Duitse wiskundige Bernhard Riemann die leefde zo rond 1850. Hij deed erg veel werk waarin hij probeerde meetkunde en analyse met elkaar te combineren.

Daar is dit natuurlijk een mooi voorbeeld van....

1. Geef met een boven- en een ondersom een benadering voor de volgende oppervlaktes. Neem steeds rechthoekjes met breedte 1.
     
  a. De oppervlakte onder de grafiek van  y = √(2x + 4) tussen de lijnen x = 0 en x = 6
   

17.646 - 19.646
b. De oppervlakte onder de grafiek van  y = 6 -  1/(x  + 1)  tussen de lijnen x = 0 en x = 8
   

45.282 - 46.171
  c. De oppervlakte onder de grafiek van  y =  (1/2)x  tussen de lijnen x = 0 en x = 12
 

0.9998 - 1.9995
VERFIJNING

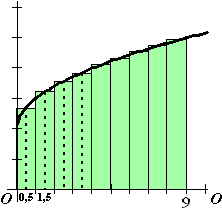
De ondersom van de linkerfiguur hierboven is een nogal ruwe benadering. Die van de rechterfiguur is al een stuk beter. De groene oppervlakte scheelt maar heel weinig met de echte oppervlakte. Dat komt omdat in de rechterfiguur rechthoekjes met breedte 1/2 zijn genomen ipv breedte 1.
De oppervlakte is dan gelijk aan   0,5 • f(0) + 0,5 • f(0,5) + 0,5 • f(1) + ... + 0,5 • f(8,5)

in de TI-83: 
L1 = 0, 0.5, 1, 1.5, ..., 8.5   en  L2 = 0,5 • (2 + √L1)  en dan sum L2 geeft een ondersom van 35,18

En de bovensom wordt  0,5 • f(0,5) + 0,5 • f(1) + ... + 0,5 • f(9) en dat geeft 36,68

35,18 < Oppervlakte < 36,68
Dat komt al aardig bij de werkelijke waarde 36 in de buurt!!!
2. Benader deze oppervlakte nog nauwkeuriger door rechthoekjes van breedte 0,25 te nemen.
   

35.600-36.350
3. De werkelijke waarde 36 zit niet midden tussen de gevonden 35,18 en 36,68 in.
Kun je daar een verklaring voor vinden?
Kun je uitleggen hoe je aan de grafiek kunt zien of de werkelijke waarde hoger of lager dan het gemiddelde van de onder- en bovensom zal zijn?
MIDDENSOM
Het gedoe met de bovensom en ondersom is nogal veel werk. Het kan ook sneller.
Hiernaast zijn rechthoekjes getekend waarvan de hoogte gelijk is aan de y die hoort bij x = 0,5 en x = 1,5 enz.
Je ziet dat je op deze manier meteen een redelijke benadering krijgt van de oppervlakte, immers er zijn nu zowel stukjes teveel als te weinig. Die zullen elkaar ongeveer opheffen.

1 • f(0,5) + 1 • f(1,5) + 1 • f(2,5) + ... + 1 • f(8,5)
geeft een oppervlakte van 36,054 en dat zit verrassend dicht bij de gezochte 36!


Een nadeel van deze MIDDENSOM is, dat we niet weten hoe ver we nog van de werkelijke waarde af kunnen zitten (dat wisten we bij de bovensom en ondersom wel, want de werkelijke waarde moest daar wel tussen zitten).

Een voordeel is echter dat dit veel minder werk is. Je hoeft nu maar één keer zo'n Riemann-som uit te rekenen.
Er is nog een tweede nadeel aan de bovensom en ondersom.
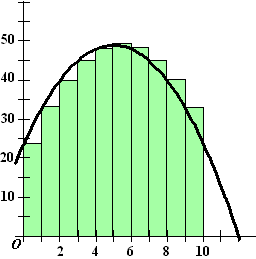
Bekijk de functie: f(x) = 10x + 24 - x2  hiernaast. We willen de oppervlakte onder de grafiek tussen x = 0 en x = 10 weten.
Maar zie hiernaast wat er gebeurt als we de functiewaarden berekenen bij x = 0, 1, 2,...9
Eerst liggen de rechthoekjes onder de grafiek maar later erboven. Er is helemaal geen sprake meer van een ondersom!
(Riemann heeft het dan ook meestal over een linkersom en een rechtersom, en het gemiddelde van die twee is nog steeds wel een goede benadering voor de oppervlakte). 

(willen we een echte ondersom berekenen dan zouden we steeds de kleinste y-waarde van de linker- en de rechterkant van elke rechthoek moeten nemen)

De middensom blijft echter nog steeds een goede directe benadering voor de oppervlakte.

4. Bereken de oppervlakte van het voorbeeld direct hierboven met behulp van een middensom.
Neem staafbreedte 1.
   

407,5
5. Bereken de oppervlakte onder de grafiek van y = sin0,5πx tussen x = 0 en x = 2 met een middensom. Neem stapgrootte 0,1.
   

1,2745
6. Koen wil de oppervlakte onder de grafiek van y = 2 - √x  tussen x = 0 en x = 9 benaderen. Hij doet dat met een middensom met stapgrootte 0,2.
In zijn rekenmachine voert hij in:
• L1 =  0.1,  0.3,  0.5,  0.7,  ...,  8.9      (dat doet hij slim via  seq(0.2X-0.1,X,1,45)  STO  L1   zoals hier staat)
• L2 =  2 - √(L1)
• L3 =  0,2 • L2
Daarna toetst hij in  List - math - sum(L3)  en hij vindt  oppervlakte -0,0051682551
Dat is wel héél weinig!!!
a. Wat is er fout gegaan?
     
  b. Hoe zou Koen dit probleem kunnen oplossen?
     
7.

     
  Hierboven zie je van twee functies de grafiek getekend. In beide gevallen wordt de oppervlakte onder de grafiek tussen x0 en x2 benaderd met behulp van een Riemann-som met twee deelintervallen. Als hoogte van de twee staafjes is gekozen: gemiddelde van de functiewaarden van de rechtergrens en de linkergrens.
     
  a. Laat zien dat de Riemann-som in beide gevallen gelijk is aan:
   
     
  b. Leg uit dat, als je het aantal staafjes vergroot, in het linkerplaatje de oppervlakte altijd te klein zal zijn en in het rechterplaatje altijd te groot.
     
  c. Je kunt de uitdrukking voor S hierboven als een soort gewogen gemiddelde van f(x0) en f((x0 + x2)/2)  en  f(x2) beschouwen. Misschien is het mogelijk door andere wegingsfactoren te kiezen een betere benadering te krijgen.
Een mogelijkheid zou zijn:
   
    De exacte oppervlakte onder de grafiek van y = x2 tussen x = 0 en x = 1 is gelijk aan 1/3.
Bepaal het getal k zó, dat deze uitdrukking van S exact deze oppervlakte weergeeft.
   

k = 4
     
8. De Golden Gate brug in San Francisco is een hangbrug waarvan de torens 1280 meter uit elkaar staan en waarvan de toppen zich 227 meter boven het water bevinden.
De brug bestaat uit een heleboel verticale dunne kabels en twee dikke kabels die in de vorm van een parabool hangen.
Het wegdek van de brug bevindt zich op 67 meter boven het water zodat de langste dunne kabel 160 meter lang is.
De kortste dunne kabel is ongeveer 5 meter lang en de horizontale afstand tussen de dunne kabels is steeds 10 meter.
Ga ervan uit dat het wegdek horizontaal loopt.

 

  Als je als x-as het wegdek kiest en op de y-as de linkertop, dan is de formule van de dikke kabel ongeveer
y = 0,0003784 • (x - 640)2 + 5
     
  a. Toon dat aan
     
  b. Bereken met een som de totale lengte van alle dunne kabels samen.
     
   

© h.hofstede (h.hofstede@hogeland.nl)