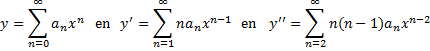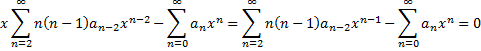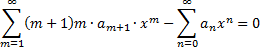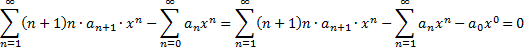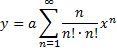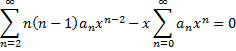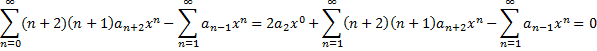ฉ h.hofstede (h.hofstede@hogeland.nl)

       
Oplossingen met reeksontwikkelingen.
       
Het is heel vaak mogelijk om oplossingen van differentiaalvergelijkingen in de vorm van reeksontwikkelingen te krijgen. Zo vaak, dat het vanaf nu niet meer nodig is dat de co๋ffici๋nten in de differentiaalvergelijkingen constanten zijn. Ze mogen vanaf nu ook best van x afhangen!
Een tweede orde homogene differentiaalvergelijking  ziet er dan in het algemeen z๓ uit;
       

p(x) • y'' + q(x) • y' + r(x) • y = 0
       
waarbij p(x) en  q(x) en r(x) dus echte functies van x zijn. We beperken ons eerst wel tot niet al te rare functies van x:  voorlopig nemen we aan dat p, q en r polynomen zijn.
Stel dat we een reeksontwikkeling hebben gevonden die een oplossing is. Neem aan dat dat een reeksontwikkeling rond het punt x = x0 is.
Dat betekent dat die gevonden oplossing van de differentiaalvergelijking er z๓ uit ziet:
       

y = a0 + a1(x - x0) + a2(x - x0)2 + a3(x - x0)3 + .... 

       
Daarin zijn alle a's constanten (die we nog moeten bepalen).
Laten we beginnen met een eenvoudig voorbeeld waarin de functies p, q en r nog constanten zijn:

Voorbeeld 1:   Los op:   xy ''- y = 0
  We gaan een reeksontwikkeling voor de oplossing  y(x)  rond het punt x0 = 0  maken.
Dat betekent dat   y =  a0 + a1x + a2x2 + a3x3 + ......
Dat geeft  y' =  a1 + 2a2x + 3a3x2 + 4a4x3 + ......   en daarna  y'' =  2a2 + 6a3x + 12a4x2 + 20a5x3 + .......
Wacht, ik begin te vermoeden dat een somnotatie misschien wel handiger werkt:
 

  We willen dit nu gaan invullen in de differentiaalvergelijking en dan gaan we proberen om al die reeksen samen in ้้n grotere reeksontwikkeling te krijgen.
Eerst maar invullen in de differentiaalvergelijking
Dat geeft: 
 

   
  Nu gaan we er eerst voor zorgen dat de machten van x in beide delen gelijk zijn aan n.  Dat kun je doen door in het eerste deel n - 1 te vervangen door m. (dus n = m + 1).  m loopt dan van 1 naar oneindig.
Dat geeft:
 

   
  Maar nu mag je al die m's natuurlijk net zo goed weer n noemen. Het zijn immers allemaal maar tellertjes. Laten we meteen de term met n = 0 uit het tweede deel los van de rest van het somteken schrijven zodat de grenzen van sommatie gelijk worden:
Dat geeft:
 

 

  Als deze reeks voor elke x gelijk aan nul moet zijn, dan moeten al die afzonderlijke co๋ffici๋nten van de verschillende x-machten nul zijn.

n = 0  geeft   a0 = 0
n = 1, 2, 3,...    geeft:   (n + 1)n • an + 1 - an = 0.    Dat is een recursievergelijking tussen an en  an + 1
 
Die kun je schrijven als  an + 1 =  an /(n(n + 1))
Kies nu a1 = a,  dan geeft de recursievergelijking:
a2 = a1/(1•2) = a/2
a3 = a2/(2•3) = a/(1•2•2•3) = a/12
a4 = a3/(3•4) = a/(1•2•2•3•3•4) = a/144
a5 = a4/(4•5) = a/(1•2•2•3•3•4•4•5) = a/2880

De oplossing van de differentiaalvergelijking is dan   y =  a • (x  + 1/2x2  + 1/12x3 + 1/144x4 + 1/2880x5 + .......)
Als je het overigens officieel met somtekens en n wilt schrijven dan moet je naar de regelmaat in die an kijken. Misschien dat je dan zelfs dit kunt verzinnen:
 

       
Voorbeeld 2.   Los op:   y ''- xy = 0
Dit lijkt nogal op het vorige voorbeeld, maar het is volledig anders!!!
  Als je nu de reeksen voor y'' en y in deze differentiaalvergelijking invult krijg je:
   
 

       
  Die tweede dat geeft xn+1  als je die x binnen dat somteken zet. Maak nu eerst van beide series  xn  door de eerste index 2 omlaag te verschuiven en de andere 1 omhoog te verschuiven.
       
 

       
  In de tweede stap hierboven is die ene term van n = 0 buiten het eerste somteken gehaald.
n = 0  geeft  2a2 = 0  dus  a2 = 0
n = 1, 2, 3...  geeft   (n + 2)(n + 1)an + 2 - an - 1 = 0  en dat is een recursievergelijking tussen an+2 en an - 1  
Die is te schrijven als   an + 2 =  an - 1  / ((n + 2)(n + 1))
Stukje uitschrijven om de regelmaat door te krijgen:

a2 = 0
a3 = a0/3•2  
a4 = a1/4•3
a5 = a2/5•4 = 0
a6 = a3/6•5 = a0/3•2•6•5  
a7 = a4/7•6 = a1/4•3•7•6
enz.

Er komen eigenlijk drie series  a's uit:
a2 = a5 = a8 = .... = 0
a3, a6, a9, .... hangen allemaal van a0 af.
a4, a7, a10, ...  hangen allemaal van  a1 af.

De uiteindelijke oplossing is     y =  a0 + a1x  + 1/6 • a0x3  + 1/12 • a1x4  + 1/180 • a0x6  + 1/504 • a1x7 + ....
       
       
Speciaal geval:    De Eulervergelijking
(Heeft die man zich dan overal mee bemoeid....?  Ik ben bang van wel.....)

De Eulervergelijking is een speciaal geval. Hij ziet er z๓ uit:    px2y''  + qxy'  + ry = 0
Zie je al wat er gebeurt als we een reeksontwikkeling rond x = 0 maken en die invullen?

Precies!  
Dan worden alle machten van x direct gelijk aan xn  en krijg je dus direct een vergelijking met overal alleen maar  an 
Vul dat zelf maar in:  je krijgt  an • (pn(n - 1) + qn + r) = 0
Dat betekent dat an nul moet zijn (de stomme oplossing) OF dat dat tweede deel nul is, en dat is een stuk interessanter.
Dat tweede deel is  pn2 + (q - p)n + r = 0 en dat is een kwadratische vergelijking in n. Dat heeft in het algemeen 2 oplossingen voor n,  en de oplossing van de differentiaalvergelijking is dan een combinatie van  xn1  en xn2  

Nou ja..... twee oplossingen......
Natuurlijk zijn er weer drie gevallen voor de kwadratische vergelijking:

1.  Twee oplossingen:  D > 0
In dat geval zijn er inderdaad, zoals hierboven al stond, twee verschillende n1 en n2 te vinden dus is de algemene oplossing
y = A • xn1 + B • xn2     waarbij A en B van de beginvoorwaarden afhangen.

Voorbeeld 3:  Los op   x2y'' - 7y'  - 16y = 0  met   y(1) =  -1  en  y'(1) = -34    
De vergelijking hierboven wordt   n2 - 8n - 16 = 0  ⇒  (n - 10)(n + 2) = 0  ⇒   n = 10  ∨  n = -2 
De algemene oplossing is  y = Ax-2 + Bx10   en de beginvoorwaarden leveren dan A = 2 en B = -3
De oplossing wordt   y = 2x-2 - 3x10  
In de reeksontwikkeling zijn dus alle an  gelijk aan nul, behalve  a-2 en a10.
       
2.  E้n oplossing:  D = 0
In dat geval vinden we maar ้้n oplossing, maar we willen er toch wel erg graag 2.  Ok้:  daar komt ie:
       

de tweede oplossing (naast  xn)  is  xn • lnx
       
Voorbeeld 4:    Los op   x2y''  + 5y'  + 4y  = 0
De vergelijking voor n wordt   n2 + 4n + 4 = 0  ⇒  (n + 2)2 = 0  ⇒  n = -2
De algemene oplossing is dan  y =  A • x-2  + B • x-2 • lnx
       
3.  Geen (of eigenlijk twee complexe) oplossingen:  D < 0
We vinden dan de twee complexe oplossingen  n = a ฑ bi  maar die kun je met een trucje re๋el krijgen, kijk maar;

En daar heb je de twee re๋le oplossingen al!
De algemene oplossingen is dan   y = xa • (Acos(blnx) + Bsin(blnx)) 

Voorbeeld 5:    Los op   x2y'' - 3xy'  + 8y  = 0
De vergelijking voor n wordt   n2 - 4n + 8 = 0 ⇒  (n - 2)2 =  -4  ⇒  n = 2 ฑ 2i    
De algemene oplossing is dan   y = x2 • (Acos(2lnx) + Bsin(2lnx))

Ja maar.....
Er is een nogal grote MAAR aan bovenstaande oplossingen op te merken. Dat zit hem in het feit dat er nu in de oplossing ook ineens best gebroken machten van x kunnen voorkomen (als n bijv. 1/2 is)  of de logaritme van x (als n complex is).
Maar dat betekent dat die oplossingen niet bestaan voor x < 0.
Wat moeten we doen als we oplossingen willen hebben die ook voor x < 0 bestaan?
 
Het antwoord is zo logisch dat je het zomaar zelf zou kunnen verzinnen:
   

stap over op  -x   in plaats van x
   
Neem de nieuwe variabele  ξ = -x
Dan neem je voor y de nieuwe functie ψ(ξ) = y(x) = y(-ξ)
Dan is  ψ'(ξ) = -y'(x)  en  ψ''(ξ) = y''(x)

De vergelijking  px2y''  + qxy'  + ry = 0  wordt dan:
pξ2ψ'' - q • -ξψ'  + rψ = 0  
ofwel gewoon weer:   pξ2ψ'' + qξψ'  + rψ = 0
       
Deze vergelijking los je op de oude vertrouwde manier op, en bij de eindoplossing ψ(ξ)  transformeer je de hele boel gewoon weer terug naar y en x.

Voorbeeld 5.   x2y''  + 21/2xy' - y = 0
De n-vergelijking wordt:  n2 + 11/2n - 1 = 0  ⇒ (n - 1/2)(n + 2) = 0  ⇒  n = 1/2  ∨  n = -2
De algemene oplossing is dan   y =  A • x1/2 + B • x-2 
Maar dat eerste deel bestaat niet voor x < 0
Overstappen op ξ en ψ  geeft dezelfde vergelijking dus dezelfde oplossingen    ξ1/2 en  ξ-2 
x < 0  geeft  ξ > 0  dus de nieuwe oplossing  ξ1/2  bestaat wel als x < 0
Terug naar x:    ψ = ξ1/2   geeft   y = (-x)1/2   Dus voor x < 0 wordt de algemene oplossing     y =  A • (-x)1/2 + B • x-2 

Ach, je had net zo goed gewoon de absolute waarde van x kunnen nemen in plaats van al dat gedoe met die y en die x.

samengevat:
oplossingen van   px2y'' + qxy'  + ry = 0:
pn2 + (q - p)n + r = 0
 
•  y = A |x|n1  +  B |x|n2  
•  y =  |x|n • (A + B ln |x|)    
•  y =  |x|a • (Acos(bln|x|) + Bsin(bln|x|))   		(n1 en n2 re๋el)
(n  re๋el)
(n = a ฑ bi)
       

ฉ h.hofstede (h.hofstede@hogeland.nl)