© h.hofstede (h.hofstede@hogeland.nl)
Raaklijnen vanaf een punt buiten de grafiek.
       
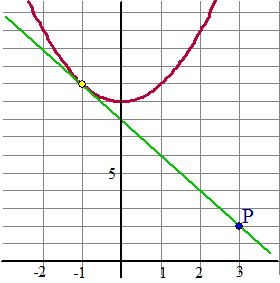
Hiernaast zie je de grafiek van y = x2 + 9  en daarnaast het punt P(3,2). Door P is een lijn getekend die de grafiek raakt (de groene lijn hiernaast). De vraag is nu:  hoe vinden we een vergelijking van die groene lijn, en hoe vinden we dat gele raakpunt?

Eigenlijk hebben we hier te maken met twee elkaar rakende grafieken (de rode en de groene). En daar hebben we het al uitgebreid in een vorige les over gehad. De conclusie was daar:

   

De grafieken van f en g raken elkaar:

 

 

1.   f '= g'

2.  f ' = g'
       
In dit geval is de ene grafiek die van y = x2 + 9  en de andere is een rechte lijn, waarvan je hopelijk weet dat de formule y = ax + b is.
f  = g  geeft dan   x2 + 9 = ax + b
f ' = g'   geeft dan  2x = a

En nou zitten we vast......
Dat zijn namelijk twee vergelijkingen met drie onbekenden, en dat valt niet op te lossen. Vanwege de onderste vergelijking zou je de a in de bovenste overal door 2x kunnen vervangen, maar dan hou je dus één vergelijking met twee onbekenden (x) en (b) over.

Maar NATUURLIJK zitten we vast!!!

Er zijn immers oneindig veel rechte lijnen die de grafiek van f raken! We hebben nog helemaal nergens in het verhaal gebruikt dat die lijn door punt P moet gaan!

Laten we dat snel gaan toevoegen....
Als de lijn door P moet gaan, dan moet de vergelijking kloppen als we de coördinaten van P(3,2) invullen in de vergelijking van de lijn (y = ax + b). Dat geeft  2 = a • 3 + b  ofwel  b = 2 - 3a. En daar is al de derde vergelijking die we nodig hebben.
Er is dus nu het stelsel van 3 vergelijkingen:   x2 + 9 = ax + b  en  2x = a  en   b = 2 - 3a en dat is wél op te lossen.
Vul de derde in voor b van de eerste en je hebt over  x2 + 9 = ax + 2 - 3a  en  a = 2x 
Vul nu a = 2x in in de eerste en er staat x2 + 9 = 2x • x + 2 - 3 • 2x 
Dat geeft  x2 - 6x - 7 = 0 ⇒ (x - 7)(x + 1) = 0  ⇒ x = 7  ∨  x = -1

Het hierboven getekende raakpunt ligt dus precies bij x = -1.
Dat geeft vervolgens a = 2x = -2  en  b = 2 - 3a = 8 dus de raaklijn is de lijn  y = -2x + 8

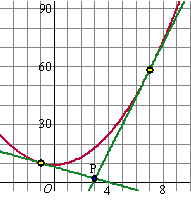
x = 7 geeft nog een tweede raaklijn:  y = 14x - 40 en in de uitgezoomde grafiek hiernaast zie je dat er inderdaad zo'n tweede mogelijkheid is voor een raaklijn door P, die de grafiek raakt in het punt (7, 58).

   
raaklijn door P(xP, yP) aan de grafiek van f:
   
• ax + b = f
• a = f '
• axP + b = yP
       
   
  OPGAVEN
   
1. examenvraagstuk VWO Wiskunde B, 1995.

De functie  f  met domein R is gegeven door:  f :  x →  4 - x2   
Punt A ligt zo op de y-as dat de raaklijnen door A aan de grafiek van f onderling loodrecht zijn.

Bereken de y-coördinaat van A.
       

4,25
2. examenvraagstuk VWO Wiskunde B, 2001.
         
  De functie f is gegeven door:
 

         
  De lijn l door het punt (0,1) raakt de grafiek van f
Stel een vergelijking op van l
         
3. Gegeven is de functie  f(x) = p√x
Een lijn door  (-q, 0)  raakt de grafiek van f
De x-coördinaat van het raakpunt blijkt onafhankelijk van p te zijn.
 
  a. Toon dat aan, en druk die x-coördinaat uit in q.    
       

x = q
  b. Leg zonder berekeningen uit waarom het logisch is dat die x-coördinaat niet van p afhangt.
         
4. Gegeven is de parabool y = x2  en het punt P(15, 7)
Een lijn door P snijdt de parabool loodrecht.
Bereken de coördinaten van het snijpunt.
       

(3, 9)
5. Welke lijn door de oorsprong raakt de grafiek van  y = √(2x - 4) ?
         
         
       

© h.hofstede (h.hofstede@hogeland.nl)