© h.hofstede (h.hofstede@hogeland.nl)
De afstand van een punt tot een vlak.
   
Waarschijnlijk is het handig om eerst deze les over de loodrechte stand door te nemen, die heb je namelijk nodig bij wat er nu komt.
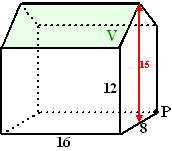
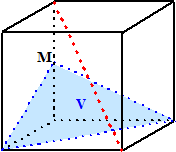
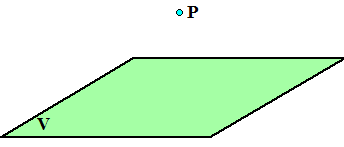
Goed, nu je alles weer weet over een lijn die loodrecht op een vlak staat kunnen we dat mooi gebruiken om de afstand van een punt tot een vlak te berekenen.

Neem punt P hiernaast dat ergens boven vlak V zweeft.

De vraag is:  "Hoe ver erboven?"
   
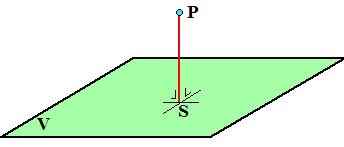
Om die vraag te beantwoorden moet je de kortste afstand van P tot V berekenen. En nou komt het:  die kortste afstand vind je als je van P loodrecht naar V gaat.
Teken dus een lijn van P loodrecht op V, waar die V snijdt noem je punt S (dat heet ook wel de projectie van P op dat vlak). De gezochte afstand is de lengte PS.
(Hiernaast zie je, dat PS loodrecht op V staat als hij loodrecht op twee snijdende lijnen uit V staat)
   
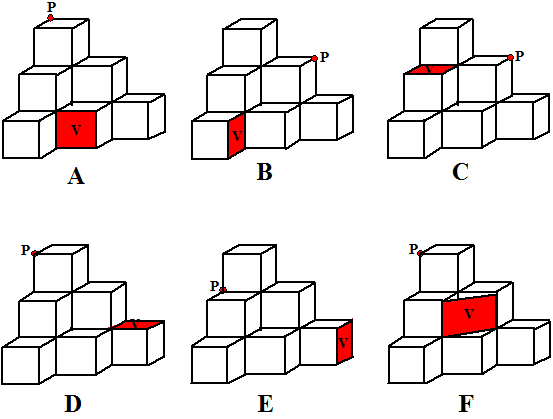
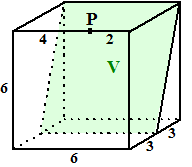
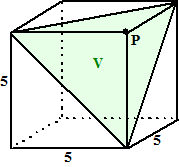
Vaak zie je in één oogopslag wel welk lijnstuk PS dat moet zijn, maar af en toe is het wat lastiger.
Eerst maar even wat makkelijke gevallen......
   
   
1. Hieronder staan zes stapelingen van kubussen met ribben 4 cm.
Bereken elke keer de afstand van punt P tot vlak V.
   
 

   
 
A:8,  B:4,  C:0,
D:8,  E:12,  F:4√2
   
2. Bereken in de onderstaande figuren de afstand van punt P tot vlak V.
       
 

  a. b. c.
 

3√2

8/5√5

2√2
       
 

  d. e. f.
 

14,4

12/5√5

5/3√3
       
 
   
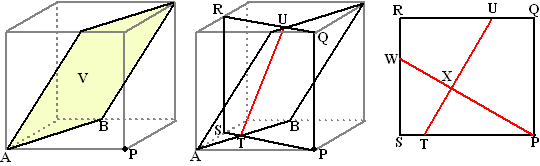
Moeilijker gevallen.

Soms is het niet zomaar in één keer te zien welk lijnstuk PS nou is.
In zulke gevallen is het vaak handig om eerst maar eens een vlak te tekenen door P dat loodrecht staat op één van de lijnen in V, en daarna in dat getekende vlak een lijnstuk te vinden dat ook nog loodrecht op een andere lijn uit V staat.
   

   
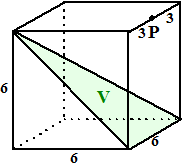
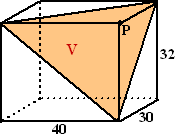
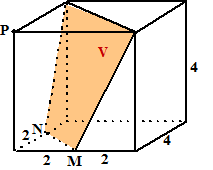
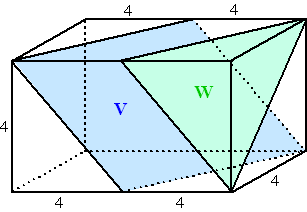
Stel dat je in de linkerfiguur hierboven de afstand van punt P tot vlak V moet berekenen (de kubus is erbij getekend om aan te geven hoe vlak V ligt)
Teken dan eerst een vlak PQRS loodrecht op bijvoorbeeld AB. Dat is zo als PS loodrecht op AB staat.
Dat geeft snijlijn TU.
Teken vervolgens (rechterfiguur) in dat vlak PQRS een lijn van P loodrecht op TU.  Dan staat die lijn dus loodrecht op TU én op AB dus op twee lijnen uit V, dus is PX de gezochte afstand.

En dan maar hopen dat je alle lengtes kunt gaan berekenen.....
   
Voorbeeld uitgewerkt.  
   
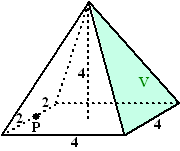
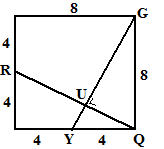
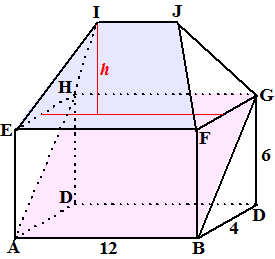
Neem aan dat de kubus uit het  voorbeeld ribben van 8 cm heeft, en dat B het midden is van de ribbe waarop hij ligt.
Het bovenvlak staat hiernaast getekend.
GY2 = 42 + 82  ⇒ GY = √80
In driehoek GYQ geldt:  √80 · QU = 4 · 8 = 32
Dus  QU = 32/√80 = 1,6√5
Op precies dezelfde manier (met zo'n zelfde tekening) geldt in het ondervlak dat AT =  1,6√5
Dus daarin is  ST2 = 42 - (1,6√5)2 =  3,2  dus ST = 0,8√5

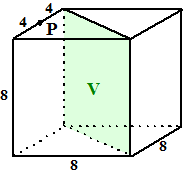
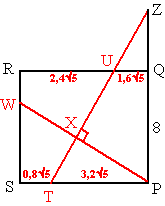
Teken vervolgens vlak  PQRS. Zie hiernaast.
Daarin is QR = √80 = 4√5.
Verder is TU verlengd, en gesneden met het verlengde van PQ.

De driehoeken ZUQ en ZTP zijn gelijkvormig.
Dan geldt  UQ/TP = ZQ/ZP 
ofwel  1,6√5/3,2√5 = 1/2 = ZQ/(ZQ + 8)
daaruit volgt  2ZQ = ZQ + 8 ⇒  ZQ = 8
Dan is ZT = √(162 + (3,2Ö5)2) = √307,2
In driehoek ZTP geldt nu  ZT ·  PX = ZP · PT
Dus PX = (ZP · PT)/ZT = (16 ·  3,2√5)/√307,2 ≈ 6,53.

   
       
3. Bereken in de balk hiernaast de afstand van punt P tot vlak V.

     

19,2
       
4. Van een kubus met ribben 4 zijn M en N de middens van twee ribben.
Bereken de afstand van vlak V tot punt P in de figuur hiernaast.

     

22/3
       
De afstand van een lijn tot een vlak.
   
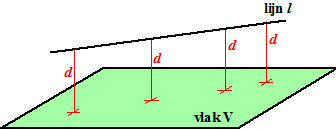
Omdat een lijn oneindig lang is, kun je het alleen maar hebben over de afstand van een lijn tot een vlak als die lijn evenwijdig aan dat vlak is. Immers als dat niet zo is, dan zullen lijn en vlak elkaar ergens snijden en is de afstand nul.

Als een lijn inderdaad  evenwijdig is aan een vlak is de afstand makkelijk te bepalen:

 

kies een willekeurig punt van de lijn
bereken de afstand van dat punt tot het vlak.
 
Immers de afstand tot het vlak is voor alle punten van de lijn gelijk.
   
De afstand van een vlak tot een vlak.
   
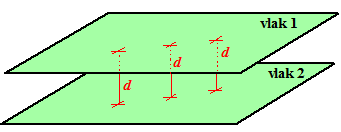
Daarmee gaat het al precies hetzelfde. Omdat vlakken oneindig groot zijn kun je het alleen maar hebben over de afstand van een vlak tot een vlak als die twee vlakken evenwijdig zijn.

In dat geval gebruik je de methode:
 

kies een willekeurig punt van het ene vlak
bereken de afstand van dat punt tot het andere vlak
 
   
       
5. Bereken in de kubus hiernaast de afstand van de rode  lijn l tot het blauwe vlak V.

Laat eerst duidelijk zien dat l evenwijdig is aan V.

Daarbij zijn de ribben van de kubus gelijk aan 12, en is M het midden van een ribbe.

     

3,46
       
6. Bereken in de balk hiernaast de afstand tussen de vlakken V en W in twee decimalen nauwkeurig.
     

2,31
       
7. Hiernaast zie je een huis met een schilddak.

   
  a. Voor welke dakhoogte h zijn de vlakken EFIJ en ABGH evenwijdig?
 

h = 3
  b. Bereken voor deze dakhoogte de afstand tussen deze beide vlakken in twee decimalen nauwkeurig.
 

3,33
     
       
8. examenvraagstuk VWO Wiskunde B, 1988.
       
  Van het prisma dat hieronder staat afgebeeld is gegeven:
∠AOC = ∠AOD = ∠COD = 90º
BC // AO
BC = CO = 8, AO = 1 en DO = 4.

De lijn l  gaat door B, snijdt de lijn EG en snijdt de lijn OD in punt P.

   
  a. Bereken OP.
   

4,5
  Punt Q ligt op het lijnstuk BG en punt R ligt op het lijnstuk AE.
Lijn QR is evenwijdig aan het vlak ABC.
QR = 10.
     
  b. Bereken de afstand van lijn QR en het vlak ABC.
 

0,5
   
   

© h.hofstede (h.hofstede@hogeland.nl)