© h.hofstede (h.hofstede@hogeland.nl)

Boek II, propositie 9.
       

Als M  het midden van AB is, en C een ander punt op AB,
dan is de som van de vierkanten op AC en CB 
tweemaal zo groot als de som van de vierkanten op AM en MC.

       
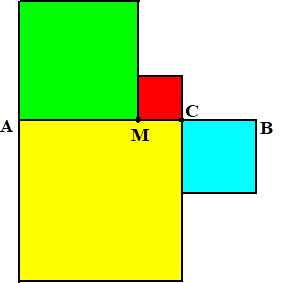
In de figuur hiernaast staan vier vierkanten waarvoor deze propositie zegt: :    geel + blauw = 2 • (groen + rood)

 

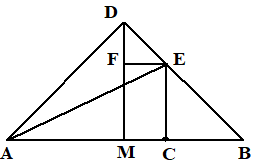
Teken MD loodrecht op AB en even lang als AM.  (I-11) en (I-3)
Teken CE parallel aan DM en EF parallel aan AB.  (I-31)
Teken AE.

In driehoek AMD is AM = MD dus de basishoeken zijn gelijk  (I-5)
Omdat de hoek bij M 90º is zijn beide andere hoeken 45º
Op dezelfde manier is ook MBD een driehoek van 45-45-90.

Dan zijn DFE en ECB ook 45-45-90  (F-hoeken)  (I-29)

Met v bedoel ik hierna het vierkant:
v(AM) = v(MD)
Dus  v(AM) + v(MD) = 2 • v(AM)

v(AD) = v(AM) + v(MD)  (Pythagoras)   (I-47)
dus  v(AD) = 2 • v(AM)		  

       
Op dezelfde manier geldt in driehoek DFE dat  v(DE) = 2 • v(FE) en dat is ook 2 • v(MC)

Dus v(AD) + v(DE) = 2 • (v(MC) + v(AM))
Maar v(AE) = v(AD) + v(DE)  (Pythagoras, want hoek ADE is 90º)   (I-47)
Dus  v(AE) = 2 • (v(MC) + v(AM))
Maar ook v(AE) = v(AC) + v(CE)  (Pythagoras want hoek ACE is 90º)   (I-47)
       
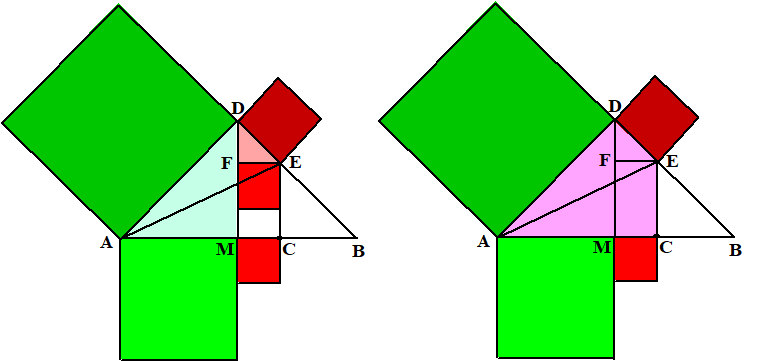
Eigenlijk is het best slim wat Euclides doet; zie de figuur hieronder:
Hij gebruikt Pythagoras in de lichtgroene en lichtrode driehoek om te laten zien dat de donkergroene en donkerrode vierkanten het dubbele zijn van de groene en rode.
Daarna koppelt hij via de paarse driehoeken rechtsonder die rode en groene vierkanten aan de vierkanten op AC en CE (=CB).
       
       
 
       
Algebraïsch staat hier eigenlijk  (a - b)2 + (a + b)2 = 2 • (a2 + b2)    (met a = AM en  b = MC)
       

© h.hofstede (h.hofstede@hogeland.nl)