© h.hofstede (h.hofstede@hogeland.nl)
De oppervlakte onder een parameterkromme.
       
   
Normaal berekenen we oppervlaktes onder grafieken door een integraal op te stellen. Maar bij parameterkrommen is dat niet zo maar te doen omdat we niet "één vergelijking" hebben.
Deze les zullen we bekijken hoe het toch kan.
       
Daarvoor gaan we terug naar de basis van oppervlakten uitrekenen, en dat was dat we een oppervlakte verdeelden in allemaal rechthoekjes, waarvan we vervolgens de oppervlaktes optelden.

Zoals in de figuur hiernaast.

De breedte van die rechthoekjes was dx en de hoogte was y dus de oppervlakte was ydx. Als we al die ydx-en bij elkaar optelden dan kwam dat neer op een integraal opstellen.

Nou, dat kan nog steeds. Waarom niet?

       
Ook als die rode grafiek hiernaast een parameterkromme is, geldt nog steeds dat de oppervlakte de som van al die ydx is.

Om die uit te rekenen gebruiken we weer de tactiek die we eigenlijk altijd bij parameterkrommen toepassen:
       

Druk alles uit in t
       
Die y uitdrukken in t zal wel lukken, want daar heb je gewoon een formule voor in de opgave staan.
om dx ook in t uit te drukken gebruik je dat dx/dt = x'(t)  dus is  dx = x'(t)dt  en daar kun je een formule voor opstellen.

De integratiegrenzen.
 
Denk erom dat ook de integratiegrenzen in t moeten worden uitgedrukt.
Daarbij moet je er goed op letten dat de dx van de rechthoekjes wel positief wordt.
Dat betekent dat je in de figuur hiernaast van links naar rechts moet gaan, dus van punt P naar punt Q.

Ook als bij P een hogere t staat dan bij Q. Als dat zo is krijg je een integraal waarvan de onderste grens groter is dan de bovenste!
 

     
Voorbeeld.

De parameterkromme in de figuur hiernaast wordt gegeven door:		  

Denk erom: de blauwe getallen zijn t-waarden!
Als je de oppervlakte van de rechterhelft wilt uitrekenen, dan kun je rechthoekjes erin denken zoals er hier eentje is getekend.
De oppervlakte van zo'n rechthoekje is dan xdy
Een heleboel zulke rechthoekjes geeft een integraal. Om dy positief te laten zijn moet je in de figuur "van onder naar boven" de kromme volgen, dus van t = 0
naar t = π.

x = sint
dy = y 'dt = 2sintdt

dat geeft samen de volgende integraal:
 
       
           
  OPGAVEN
           
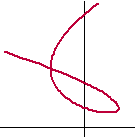
1. Hiernaast zie je de kromme gegeven door x(t) = t3 - 3t  en  y(t) =  t2 + t + 1.
Bereken de oppervlakte van het lusje.

 

           
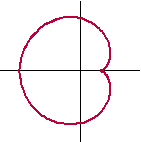
2. Hiernaast zie je de kromme gegeven door x(t) = 2cost - cos2t  
en  y(t) = 2sint - sin2t.

Bereken de oppervlakte van het binnengebied van deze kromme.

Geef je antwoord in één decimaal nauwkeurig

           
3. Bereken de oppervlakte van het vlakdeel dat wordt  ingesloten door de y-as en de kromme K die wordt gegeven door  x(t) = t2 - 2t  en  y(t) = √t
         

 8/15√2 

4. Bereken de oppervlakte van het vlakdeel dat wordt  ingesloten door de x-as en de kromme K die wordt gegeven door  x(t) = 1 + et   en  y(t) = t - t2
Geef je antwoord in twee decimalen nauwkeurig.
         

 3 - e 

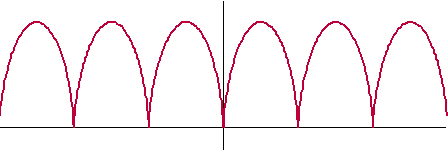
5. Een cycloïde wordt gegeven door  x(t) = t - sint  en y(t) = 1 - cost.
Hieronder zie je de grafiek.
           
 

           
  Bereken algebraïsch de oppervlakte onder één zo'n bergje.
         

 3π 

           
6. De ellips E wordt gegeven door:  x(t) = -4cost  en  y(t) = 1 + 2sint
Bereken de oppervlakte van het vlakdeel dat wordt begrensd door de ellips en de positieve coördinaatassen.
           
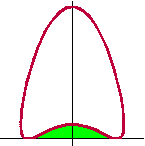
7. Hiernaast zie je de kromme K gegeven door:

 
         
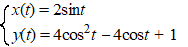  Bereken de oppervlakte van het groen gekleurde vlakdeel in één decimaal nauwkeurig.
           
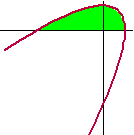
8. Hiernaast zie je de kromme K gegeven door:

 
         
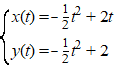  Bereken de oppervlakte van het groen gekleurde vlakdeel.
           
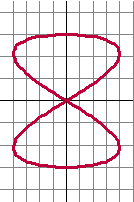
9. De 8 hiernaast heeft vergelijkingen:

   
 
         
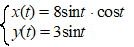  a. Bereken de oppervlakte van het vlakdeel dat door de 8 wordt omsloten.
         
  b. Bereken de inhoud van het lichaam dat ontstaat als de 8 wordt gewenteld om de y-as in één decimaal nauwkeurig.
           
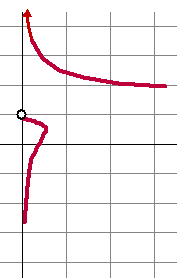
10. Gegeven is de volgende parameterkromme:

 

         
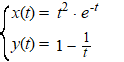  Bereken algebraïsch de oppervlakte, ingesloten door deze kromme, de x-as, de y-as en de lijn y = 0,5.
 
         
         
           
11. Kromme K wordt gegeven door:   x(t) = 1 - sin t  en  y(t) = cos 2t  met t in  [a,b]
           
  a. Kies a en b zó dat de hele kromme precies één keer doorlopen wordt, en plot K.
           
  De kromme K en de x-as sluiten samen een vlakdeel  V in.
           
  b. Bereken de omtrek van V.
           
  c. Bereken de oppervlakte van V.
           
12. Gegeven is de parameterkromme K door:
 

           
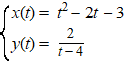  a. Onderzoek en teken kromme K
           
  b. Geef de vergelijking van de raaklijn aan K in het punt (12,2)
           
  c. Bereken de oppervlakte van het vlakdeel, ingesloten door K en de y-as.
           
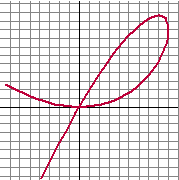
13. Gegeven is parameterkromme K door:   x(t) = -t2 + 6t  en  y(t) = -1/3t3 + 2t2
         

  a. Onder welke hoek snijdt K zichzelf?
         
  b. Bereken de oppervlakte van het vlakdeel dat geheel wordt ingesloten door K.
         
  c. Voor welke p geldt dat de lijn  y = 2x - p de grafiek van K raakt?
           
14. Examenvraagstuk.

 
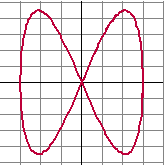
  Ten opzichte van een rechthoekig assenstelsel is voor t uit [0, 2π] de kromme K gegeven door:   x(t) = 3 • sint  en  y(t) = 41/2 • sin2t

         
  a. Bereken de coördinaten van de punten van K waarin de raaklijn aan K evenwijdig is aan een van de coördinaatassen.
         
  b. Toon aan dat de coördinaten van de punten van K voldoen aan: 
y2 = x2 (9 - x2)
           
  c. Bereken de oppervlakte van het in het eerste kwadrant gelegen vlakdeel dat begrensd wordt door K en de x-as.
           
       
         

© h.hofstede (h.hofstede@hogeland.nl)