 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
Nog meer natuurkundige toepassingen. |
|
|
|
1. Arbeid. |
|
|
De arbeid die een
kracht verricht is gelijk aan de grootte van die kracht vermenigvuldigd
met de afstand waarover die kracht werkt. (Dat is het natuurkundige
begrip van arbeid, niet het alledaagse: als je uit alle macht een uur
lang tegen een stenen muur staat te duwen heb je natuurkundig geen
arbeid verricht, alhoewel je waarschijnlijk het zweet over je rug voelt
stromen!)
De formule die men meestal gebruikt is W = F
×
s waarin W de arbeid
is, F de kracht en s de afstand.
Als je integralen een beetje doorkrijgt dan snap je het probleem
intussen natuurlijk al wel....
| |
|
Hoe is het als
de kracht niet constant is, maar van de afstand
afhangt? |
|
| |
En ook de oplossing gaat je hopelijk
intussen een beetje bekend voorkomen:
Verdeel de afgelegde weg in kleine stukjes ds.
Over één zo'n stukje ds is de kracht dan wél ongeveer constant,
namelijk F(s), dus dW = F(s)ds
Tel dan al die arbeidjes dW bij elkaar op met een integraal:
|
| Voorbeeld
1: De ontsnappingssnelheid voor de aarde. |
| |
|
Als je een voorwerp (een kogel of
zo) wegschiet van de aarde, dan trekt de aarde die kogel terug. De aarde
verricht arbeid op de kogel. Maar hoe verder de kogel weg is, des te
kleiner wordt de aantrekkingskracht van de aarde. De vraag is nu:
hoeveel bewegingsenergie moeten we de kogel meegeven om al die
"terugtrekarbeid" van de aarde te overwinnen?
De kracht tussen twee voorwerpen met massa M en m is gelijk aan:
|
 |
Daarin is G een constante (6,68 •
10-11 ) en M en m de massa's in kg en r de
afstand in meter en F de kracht in Newton.
Maarde = 5,97 • 1024 en Raarde
= 6378 km.
Dat betekent dat F(r) = 3,99 • 1014 • m
• 1/r2
Op een klein stukje dr is deze kracht ongeveer constant
en verricht een arbeid dW.
De totale verrichte arbeid door de aarde op de kogel als de kogel van
r = R naar r = ∞ gaat is dan
gelijk aan:
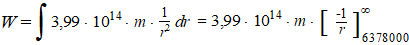
6,25 • 107 m ⇒
v2 = 1,25 • 108 ⇒
v = 11183 m/s =
11,2 km/s.(in werkelijkheid nog groter omdat we de
luchtwrijving hebben verwaarloosd). |
| |
|
| Voorbeeld
2: De potentiële energie van een geladen bol. |
| |
|
Hoeveel elektrische energie zit er opgeslagen
in een bol met straal R en lading Q op het oppervlak? Dát er energie in
is opgeslagen zal duidelijk zijn: laat alle lading "los" van de bol en
het zal uit elkaar vliegen omdat gelijke ladingen elkaar afstoten. De
hoeveelheid energie die opgeslagen zit in zo'n bol kun je berekenen door
hem langzaam op te bouwen".
Dat gaat als volgt.
Begin met een lege bol en breng een ladinkje dQ vanaf oneindig naar het
oppervlak van de bol. Dan nog een ladinkje, dan nog een, enz. Net zolang
tot de totale lading Q op de bol zit. |
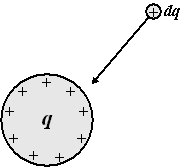 |
Stel dat er op de bol op een
gegeven moment al lading q aanwezig is. Hoeveel energie kost het
dan om een extra ladinkje dq erheen te brengen?
Elektrische ladingen met hetzelfde teken stoten elkaar af met de zgn.
"Coulombkracht":
Daarin is k een constante (8.99 • 109), F de kracht
in Newton, q en dq de ladingen in Coulomb, en r de
afstand in meter.
over stukje dr kost dat kracht Fdr, dus in totaal
kost het:
Om alle stukjes dq op hun plaats te krijgen moeten we nogmaals
al deze dW's bij elkaar optellen:
En daarmee hebben we een formule voor de elektrische energie
(potentiële energie) van zo'n bol.
Doe er vooral iets leuks mee..... |
| |
|
|
OPGAVEN |
|
|
| 1. |
Om een veer vanuit ruststand in te drukken is
een kracht F = -c • u nodig, waarbij c een
constante is, afhankelijk van het soort veer, en u de
uitwijking vanaf de ruststand van de veer. |
| |
|
|
|
|
|
|
|
| |
a. |
Een bepaalde veer heeft c =
40 N/m.
Hoeveel arbeid moet je verrichten om deze veer vanuit
rustpunt 12 cm in te drukken? |
|
| |
|
|
|
| |
b. |
Een jongetje heeft een katapult
gemaakt door een veer met c = 30 N/m 15
cm in te drukken en dan met een haakje vast te zetten. Daarna
legt hij er een knikker (van 20 gram) voor en maakt het haakje
los. De veer ontspant zich en zet alle opgeslagen veerenergie om
in bewegingsenergie van de knikker (E = 1/2mv2)
Welke snelheid heeft de knikker op het moment dat hij losraakt
van de veer? |
|
| |
|
|
|
|
|
|
|
| 2. |
Een touw weegt 0,8
kg/m. Het is 2 meter lang. Het ligt in zijn
geheel op de grond. Iemand pakt een uiteinde vast en gaat het
touw langzaam optillen. Dat doet zij totdat het uiteinde 2 meter
boven de grond is, en het andere uiteinde dus precies de grond
raakt.
Om het bovenuiteinde van het touw van hoogte h naar
hoogte h + dh te brengen moet ze een kracht F =
m • g uitoefenen. (g is de
zwaartekrachtsversnelling en die is ongeveer 9,8 m/s2
en m is de massa van het touw dat al in de lucht hangt)
Dat moet over een afstand dh, dus dat kost kracht
mg • dh
Hoeveel arbeid heeft zij na afloop in totaal verricht? |
| |
|
|
|
|
|
|
|
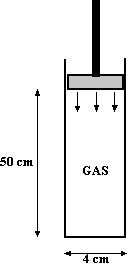
| 3. |
We bekijken een
afgesloten hoeveelheid gas in een cilindervormige buis met een
zuiger erop. De hoogte van de zuiger in het begin 50 cm, en de
doorsnede van de buis heeft straal 2 cm. De luchtdruk is overal
1 bar.
De zuiger wordt naar beneden gedrukt tot een hoogte van 25 cm.
Voor het gas in de cilinder geldt pV = c
(p is de druk in bar, V het volume in m3 en
c een constante, voor deze hoeveelheid gas gelijk aan 105). Tijdens het naar beneden drukken van de
zuiger wordt het volume kleiner dus de druk groter. Het gas gaat
een kracht naar boven uitoefenen.
Tijdens een klein stukje dh van dat naar beneden drukken
is de druk binnen de zuiger ongeveer constant. Dus kun je de
arbeid die nodig is om dat stukje af te leggen berekenen.
Hoeveel arbeid moet in totaal verricht worden om deze zuiger op
hoogte 25 cm te krijgen? |
 |
| |
|
|
|
|
|
|
|
| 4. |
Op de bodem van een 200 meter diepe mijnschacht
staat een emmer gevuld met kolen die in totaal 166 kg
weegt (emmer + kolen). Aan de emmer zit een stalen kabel die per
meter 0,2 kg weegt.
Hoeveel arbeid is er nodig om de emmer (+ kabeldeel) 200 meter
omhoog te takelen? |
| |
|
|
|
|
|
|
|
| 5. |
Een metalen ketting die 3 kg/meter
weegt en 20 meter lang is hangt in zijn geheel van een
verdieping van een flat in aanbouw naar beneden. Een bouwvakker
trekt de kabel helemaal omhoog naar de verdieping.
Hoeveel arbeid verricht de bouwvakker? |
| |
|
|
|
|
|
|
|
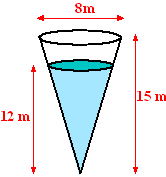
| 6. |
In een tank met de vorm
van een omgekeerde kegel met hoogte 15 meter en straal grondvlak
4 meter bevindt zich water tot op een hoogte van 12 meter.
Hoeveel arbeid kost het om al dat water uit de tank te pompen
(dus naar een hoogte van 15 meter te brengen)? |
 |
| |
|
|
|
|
|
|
|
|
|
|
|
2. Wet van Hooke |
|
|
Om materialen te testen passen
natuurkundigen vaak de zogenaamde trekproef toe. Ze klemmen een staaf
van een bepaald materiaal vast in een soort trekbank en oefenen er op de
bovenkant en de onderkant een kracht op uit. Daarbij wordt nauwkeurig
gemeten hoeveel de staaf langer wordt.
Het blijkt dat, voor niet al te grote uitrekkingen, de wet van Hooke
deze uitrekking goed beschrijft:
|
Daarin is F de trekkracht (in kN),
l de lengte van de staaf (in cm), A de oppervlakte
van de doorsnede (in cm2 ) en E een constante die van het
materiaal afhangt. Die heet de elasticiteitsmodulus of ook wel 'modulus
van Young'.
Tot zover geen probleem. Als je bijvoorbeeld een cilindervormige staaf
(doorsnede 8 cm2) van staal (E = 21000) hebt die 1,5
meter lang is, en waarop je een trekkracht van 5000N op beide
uiteinden uitoefent, dan wordt de uitrekking:
Δl = (5 • 150)/(21000
• 8) = 0,0045 cm. Niet spectaculair veel dus. |
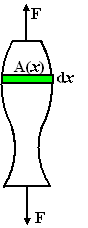
Een leuker probleem krijg je natuurlijk als je een staaf neemt waarvan
de doorsnede niet overal gelijk is, dus A(x).
De oplossing in dit geval is: neem een plakje met dikte dx. Dan
is daarvan de doorsnede wel ongeveer constant (A(x)) dus daarvan
kun je de uitrekking daarvan
berekenen.
Tel daarna al die stukjes uitrekking
met een integraal bij elkaar op.
|
 |
| |
|
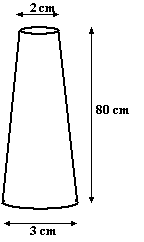
| 7. |
Iemand heeft van aluminium (E =
7000 kN/cm2) de afgeknotte kegelvorm hiernaast
gemaakt.
Op bovenvlak en ondervlak wordt een trekkracht van 10 kN
uitgeoefend. |
 |
| |
a. |
Toon aan dat voor de
oppervlakte A van de doorsnede op hoogte h vanaf het
grondvlak geldt: A(h) = 0,000123h2
- 0,0589h + 7,0686 |
| |
b. |
Bereken de uitrekking
Dl van de afgeknotte kegel. |
| |
|
|
|
|
| |
|
|
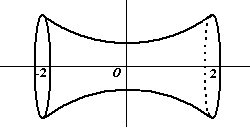
| 8. |
De parabool y =
0,2x2 + 1 met domein [-2,2] wordt gewenteld om
de x-as. Dat geeft een soort vorm als hiernaast.
Stel dat dit lichaam massief zou zijn, en gemaakt zou zijn van
staal (E = 21000) hoeveel zou het dan uitrekken als we op de
beide zijvlakken een kracht van 15 kN naar links/rechts zouden
uitoefenen? |
 |
| |
|
|
|
|
|
|
|
|
|
|
3. Radioactieve Straling. |
|
|
De hoeveelheid straling die een
radioactieve bron afgeeft is niet constant. Immers doordat
radioactieve atomen vervallen naar stabiele atomen zal het aantal
radioactieve atomen, en dus ook de intensiteit van de straling, in de
loop van de tijd afnemen. Voor de intensiteit (I), dat is afgegeven
hoeveelheid straling per tijdseenheid, op een bepaald moment (t)
geldt I(t) = I(0) • e-ct
De eenheid van de intensiteit is tegenwoordig Bequerel (Bq).
Vroeger heette het Curie. Het aantal Becquerel van een
stralingsbron is gelijk aan het aantal atomen dat per seconde vervalt.
Neem een stralingsbron met I(0) = 600 en c = 0,004.
Hoeveel straling zal deze bron afgeven tussen t = 10 en t =
100 ?
Neem een klein tijdsinterval tussen t en t + dt.
Op dat kleine interval zal I(t) ongeveer constant zijn, dus een
hoeveelheid straling I(t) • dt uitzenden.
Voor de totale hoeveelheid straling tellen we al die tijdsintervallen
bij elkaar op. Met een integraal uiteraard!
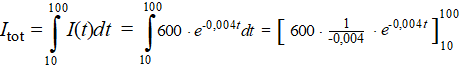
Dat is gelijk aan -15000 • e-0,4 - -15000
• e-0,04 = -10054,8 --14411,8 = 4357 Bq. |
| |
|
| 9. |
Een radioactieve bron heeft I(0) = 300
en c = 0,001 |
| |
|
|
|
|
|
|
|
| |
a. |
Hoeveel straling zal deze bron
tussen t = 100 en t = 200 afgeven? |
|
| |
|
|
|
| |
b. |
Hoeveel straling zal deze bron in
totaal afgeven? |
|
| |
|
|
|
|
|
|
|
| 10. |
Een radioactieve bron heeft
I(0) = 500 en c = 0,004.
Ik begin te meten op tijdstip t = 20 sec.
Hoelang moet ik meten totdat de bron in totaal 100000 Bq zal
hebben afgegeven? |
|
| |
|
|
|
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|