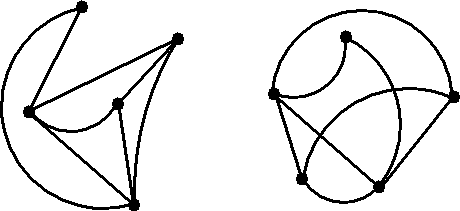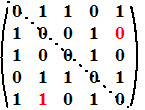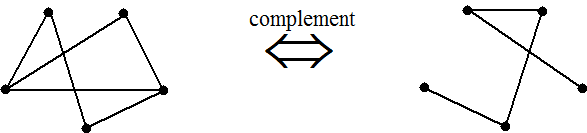© h.hofstede (h.hofstede@hogeland.nl)

Nog maar wat termen....
       
Hier volgen nog wat begrippen/termen die vaak bij grafen gebruikt worden. 't Is wel handig als je de les over de verbindingsmatrix van een graaf hebt doorgenomen want veel van deze begrippen kun  je makkelijk aan de hand van zo'n verbindingsmatrix uitleggen.
       
1.  Isomorf
       
Twee grafen noemen we "isomorf" als ze wiskundig gezien hetzelfde zijn. Dat wil zeggen dat de "structuur" van de grafen gelijk is, dus dat de knooppunten op dezelfde manier met elkaar verbonden zijn. 
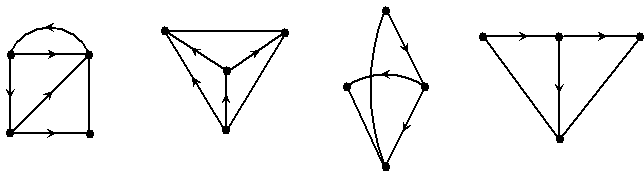
In een plaatje van een graaf betekent dat, dat het er alleen om gaat OF er een verbindingslijn tussen twee knooppunten loopt, en niet HOE die is getekend.
De twee grafen hieronder zijn bijvoorbeeld isomorf alhoewel het "plaatje" er nogal anders uitziet. Door er op te clicken kun je de kleuren van de verbindingslijnen aanzetten of uitzetten.
 

       
Je ziet dat de verbindingen inderdaad gelijk zijn. Ze zijn alleen een beetje anders getekend, en de knooppunten liggen op een andere plaats, maar de structuur is hetzelfde.
 
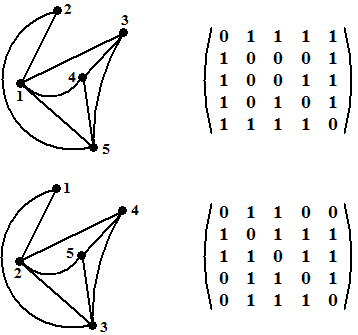
Voor de verbindingsmatrix betekent dat, dat die ook hetzelfde is.
Maar kijk daarbij wel uit:  de knooppunten kunnen best anders genummerd zijn.
Hiernaast zie je twee keer de graaf van hierboven, maar op twee verschillende manieren genummerd.
Dat betekent dat de verbindingsmatrices die ernaast staan er nogal verschillend uitzien alhoewel ze wel bij dezelfde graaf horen.....
       
2.  Gericht en Ongericht.
       
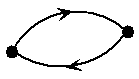
Nou, dat is erg makkelijk:  Een graaf is ongericht als ALLE verbindingslijnen ongericht zijn. Zodra er één verbinding gericht is, is de graaf dat ook.  Daarbij moet je niet flauw doen door tussen twee knooppunten twee gerichte lijnen te tekenen zoals hiernaast. Dat is natuurlijk gewoon één ongerichte verbinding!

       
Je herkent een ongerichte graaf direct aan het feit dat de verbindingsmatrix symmetrisch is in de hoofddiagonaal (die van linksboven naar rechtsonder), immers bij elke verbinding van A naar B is er ook een verbinding van B naar A. Aan de twee rode getallen in de matrix hiernaast zie je direct dat die hoort bij een gerichte graaf!

       
3.   Ingraad en Uitgraad
       
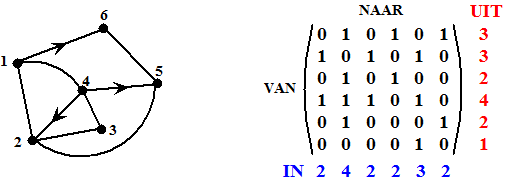
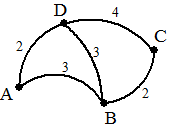
Elk knooppunt van een graaf heeft een ingraad en een uitgraad. De ingraad is het totaal aantal verbindingslijnen dat NAAR het knooppunt toe gaat. De uitgraad is het totaal aantal verbindingslijnen dat VAN het knooppunt af gaat.  Daarbij telt een ongerichte verbindingslijn dus mee bij de ingraad én bij de uitgraad van een knooppunt. Een lus telt dus ook twee keer mee.
Hieronder zie je een graaf met daarnaast de verbindingsmatrix
       

       
De uitgraad van een knooppunt vind je door de getallen in een rij op te tellen, immers dat zijn alle wegen die VAN het knooppunt gaan. De ingraad vind je door de getallen in de kolom op te tellen, immers dat zijn alle wegen die NAAR het knooppunt gaan.
Zo zie je in deze graaf/matrix dat knooppunt 4 een ingraad van 2 heeft, en knooppunt 2 een uitgraad 3.

Het knooppunt met de meeste in- en uitgraden heet trouwens het centrale punt  van een graaf. In ons voorbeeld zou dat knooppunt 2 zijn (7 in- en uitgraden)

N.B.  Bij ongerichte grafen noemen we de graad van een knooppunt vaak gewoon het aantal ingraden (of uitgraden, dat is hetzelfde). Waarom zou je alles dubbel tellen?

Een graaf waarvan alle punten dezelfde graad hebben heet trouwens  regulier.  (met alle punten van graad n wordt zo'n graaf ook wel  n-regulier genoemd).

Hier is trouwens een leuke stelling:
 
Het aantal knooppunten met oneven graad in een ongerichte graaf is even
       
Waarom is dat zo?
De som van het totaal aantal graden van alle knooppunten is even. Immers elke verbindingslijn geeft 2 graden.
De knooppunten met een even graad geven samen een even aantal graden
Dus moeten de knooppunten met een oneven graad samen ook een even aantal graden opleveren, want even + even = even
Dus moeten dat wel een even aantal knooppunten zijn (een oneven aantal keer een oneven getal is oneven)

Daarmee is trouwens meteen dit beroemde raadsel opgelost:
Op een feest schudden een aantal van de gasten elkaars handen.  Het aantal mensen dat na afloop een oneven aantal handen heeft geschud is even.
Toon dat aan.
       
       
4. Graad van Verbondenheid.
       
De graad van verbondenheid van een graaf is een getal tussen nul en één dat aangeeft hoeveelste deel van alle mogelijke verbindingen werkelijk aanwezig is in de graaf, dus:
       

       
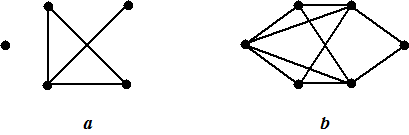
Daarbij telt een ongerichte verbinding dus voor twee. De graad van verbondenheid is dus het aantal enen in de verbindingsmatrix gedeeld door het maximale aantal enen.
Bij de graaf hierboven is de graad van verbondenheid gelijk aan  15/30 = 1/2 
Een graaf waarin alle punten direct met alle andere zijn verbonden heeft graad van verbondenheid 1.  Zo'n graaf heet ook wel  volledig.  Een volledige graaf met n knooppunten noemen we  Kn  
K2 tm K6 zien er zó uit:
       

       
De laagste graad van alle knooppunten van een  graaf geven we meestal aan met d, de hoogste graad met D.
       
5.  Complement
       
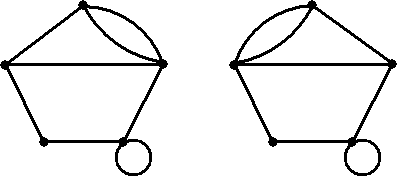
Het complement van een graaf is een nieuwe graaf die bestaat uit alle verbindingslijnen die er in de oorspronkelijke graaf NIET zijn. Een soort "tegenovergestelde graaf" dus. Hieronder zie je een graaf met zijn complement. (Ze zijn natuurlijk elkaars complement; als je het "complement van het complement" neemt, dan krijg je de graaf zelf weer).
       

       
Er bestaan zelfs zelf-complementaire grafen. Dat zijn grafen waarvan de complementgraaf gelijk is (= isomorf met) de oorspronkelijke graaf!

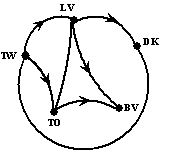
Kun jij er eentje vinden?  Ik wel!
Met de knooppunten hiernaast lukt dat best.

Click er maar op als je de oplossing wilt zien.....en ga daarna vooral ook na dat dit inderdaad een zelf-complementaire graaf is!!

       
6.  Enkelvoudige Graaf

Een enkelvoudige graaf  is een ongerichte graaf met tussen twee knooppunten hoogstens één verbindingslijn en zonder lussen.
Formeler gesteld:
•   er zijn niet twee verbindingslijnen met dezelfde eindpunten.
•   er is geen verbindingslijn met "beginpunt = eindpunt".
•   er is geen gerichte verbindingslijn.
       

 
OPGAVEN
       
1. In de economie van een land doen zich op een gegeven moment de volgende verschijnselen voor:
       
 

Daling van de koopkracht (DK)
Loonsverlaging (LV)
Toename werkloosheid (TW)
Belastingverhoging (BV)
Toename overheidstekort (TO)
       
  Tussen deze verschijnselen bestaan oorzakelijke verbanden. Hiernaast zie je van deze economie een graaf waarbij de verbindingslijnen de relatie "...heeft tot gevolg dat..." weergeven.

     
  a. Hoe is aan deze graaf te zien dat er een neerwaartse spiraal is? (dus dat de werkeloosheid alleen maar zal toenemen)
     
  b. Geef de verbindingsmatrix van deze graaf.
       
  c. Met welke van de onderstaande grafen is deze graaf isomorf?  
       

       
  Om deze crisis te bestrijden kan de overheid kiezen uit drie maatregelen:
    1.  De belastingen minder verhogen
2.  De lonen minder laten dalen door verhoging van het minimumloon
3.  De werkeloosheid minder laten stijgen door stimulering van de werktijdverkorting.
       
  d. Men wil graag de maatregel nemen die het meest centrale punt van de graaf tegenwerkt. Welke maatregel zou dat kunnen zijn?
       
  e. Bereken M2 en M + M2  en probeer vervolgens vraag d) opnieuw te beantwoorden.
       
2. De graaf hiernaast stelt de plattegrond van een pretpark voor met vier grote attracties (A t.m.D) verbonden door paden. De lengte van de paden (in honderden meters) staan bij de verbindingslijnen.

     
  a. Bereken de graad van verbondenheid.
     
  b. Stel een verbindingsmatrix op en bereken de diameter van deze graaf.
       
  De vier attracties hebben elk een eigen restaurant waar per dag respectievelijk 100, 300, 400 en 200 maaltijden worden gebruikt. Men wil bij één van de attracties een centrale keuken bouwen en van daaruit de restaurants van maaltijden voorzien.
       
  c. Bereken met een matrixvermenigvuldiging bij welke attractie de centrale keuken het best gebouwd kan worden om de afstand die de maaltijden gemiddeld moeten afleggen zo klein mogelijk te houden
       
3. Vier leerlingen hebben een systeem ontwikkeld om spiekbriefjes aan elkaar door te geven.
Klaas kan briefjes krijgen van Michel en Gerard, en geven aan Saskia.
Tussen Saskia en Michel kunnen briefjes heen en weer gegeven worden.
Michel kan briefjes geven aan Gerard.
       
  a. Teken een graaf die die briefjesverkeer weergeeft.
Wat is het totaal aantal uitgraden van Michel in de graaf van de tweestapsverbindingen?
       
  b. Wie heeft de minst centrale ligging?
       
4. a. Teken zoveel mogelijk verschillende (niet-isomorfe) minimaal verbonden ongerichte grafen met zes knooppunten.
       
  b. Welke van onderstaande grafen zijn isomorf?
       
   

       
5. a. Hoeveel 2-reguliere grafen met 5 knooppunten bestaan er?  En met 6 knooppunten?
       
  b. Hoeveel 3-reguliere grafen met 5 knooppunten bestaan er?  En met 6 knooppunten?
       
6. Voor n = 4, 6, 8, 10, ...  bestaat er altijd een 3-reguliere graaf.
Toon aan dat dat inderdaad zo is.
       
7. Toon aan dat voor een enkelvoudige graaf geldt  V £  (K nCr 2)  waarin V het aantal verbindingslijnen is en K het aantal knooppunten. Toon ook aan dat het gelijkteken alleen geldt als de graaf volledig is.
       
8. Hoeveel enkelvoudige niet-isomorfe grafen met 4 knooppunten bestaan er?
       
9. Toon aan dat voor het aantal verbindingslijnen van een zelf-complementaire graaf altijd geldt:  V = 0 of 1 (mod 4)
       
10. Leg duidelijk  uit waarom de volgende twee grafen NIET isomorf zijn.
       
 

       
11. Hoeveel verbindingslijnen heeft een k-reguliere graaf met n knooppunten?
       
12. Toon aan dat elke graaf (met minstens 2 knooppunten) altijd 2 punten van gelijke graad heeft.
       
13. Teken het complement van de volgende twee grafen:
       
 

       
     

© h.hofstede (h.hofstede@hogeland.nl)