| |
© h.hofstede (h.hofstede@hogeland.nl)
|
| |
|
|
| 1. |
De koning verveelt
zich.
Hij heeft alle naburige landen veroverd, en is uitgekeken op al zijn
vrouwen. |
 |
| |
|
|
| |
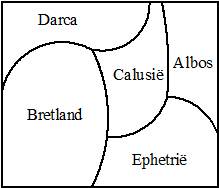
Hij gaapt eens en
kijkt tevreden naar de kaart van zijn bezittingen (zie de figuur). Zijn
paleis ligt midden in CalusiŽ. Maar liefst 5 landen en de bijbehorende 7
grensovergangen daartussen zijn in zijn bezit.
Uit verveling begint hij een graaf te tekenen met als knooppunten de
landen en als verbindingslijn de relatie "heeft een grens met" |
| |
|
|
|
| |
a. |
Welk van onderstaande
grafen zou de graaf van de koning kunnen zijn? Leg uit! |
| |
|
|
|
| |
|
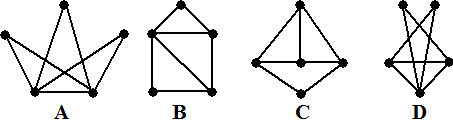 |
| |
|
|
|
| |
b. |
Stel van jouw graaf
een verbindingsmatrix M op en bereken M2 .
Leg duidelijk uit wat de getallen op de hoofddiagonaal van M2
voorstellen.
Leg nog duidelijker uit wat de andere getallen van M2
voorstellen. |
| |
|
|
|
| |
c. |
De koning gaat een
reis maken. Hij begint in CalusiŽ en kiest steeds als hij in een land is
willekeurig een buurland om naar toe te gaan (teruggaan kan dus ook!)
Bereken hoeveel verschillende routes de koning kan volgen om na 4 grenzen te zijn overgetrokken
weer in CalusiŽ te zijn. Bereken deze kans met een matrixvermenigvuldiging. |
| |
|
|
|
| 2. |
Zes teams hebben een halve
competitie van een volleybaltoernooi gespeeld, en de resultaten daarvan
staan in de matrix hiernaast. |
 |
| |
|
|
| |
a. |
Leg uit hoe je kunt zien dat alle wedstrijden
gespeeld zijn. |
| |
|
|
| |
b. |
Leg uit waarom er niet direct een winnaar kan
worden aangewezen. |
| |
|
|
| |
c. |
Men besluit daarom
tweestaps-overwinningen ook een half punt te geven. Bereken met behulp
van de tweestapsverbindingen wie de winnaar van dit toernooit wordt. |
| |
|
|
|
| 3. |
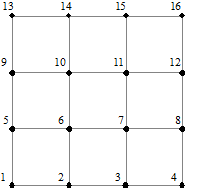
Iemand maakt een
verbindingsmatrix V voor alle 16 roosterpunten van het rooster
hiernaast. Dat wordt dus een 16 ◊16
matrix.
Welk getal zal er op de derde rij en de derde kolom van V6
staan? |
 |
| |
|
|
|
| |
|
|
|
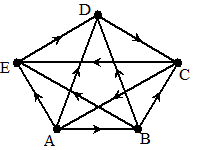
| 4. |
De graaf hiernaast geeft de
resultaten van een tennistoernooi. De pijlen geven de relatie
"heeft gewonnen van" weer.
Verzin een methode om via verbindingsmatrices de winnaar van het
toernooi aan te wijzen.
Maak daarbij ook gebruik van indirecte overwinningen. |
 |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|