|
|||||
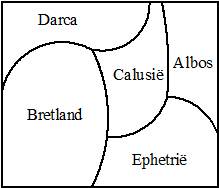
| 1. | a. | Het aantal grenzen dat de landen
hebben is : A: 2 B: 3 C: 4 D: 2 E: 3 Graaf A heeft 4-4-2-2-2 lijnen per knooppunt dus valt af. Graaf C heeft 3-3-3-3-2 lijnen per knooppunt dus valt af. B en D zouden beiden nog kunnen. |
 |
||
| b. |
 |
||||
 |
|||||
| Hoofddiagonaal:
aantal manieren om van een land naar een buurland te gaan en weer terug.
ofwel: aantal buurlanden. Andere plaatsen: aantal manieren om van een het ene land naar het andere te gaan via ťťn ander land. |
|||||
| c. |
 |
||||
| In totaal zijn er 26 mogelijke routes van C naar C. | |||||
| 2. | a. | Er staan 15 enen in
de matrix dus er zijn 15 wedstrijden gespeeld. In een halve competitie met 6 teams worden inderdaad 15 wedstrijden gespeeld. |
|||
| b. | De teams A, B, C en D hebben allemaal drie wedstrijden gewonnen en zijn dus gelijk geŽindigd. | ||||
| c. |
 |
||||
| Daaruit blijkt dat team A winnaar is geworden. | |||||
| 3. | Dat is het aantal
manieren om van (0,0) naar (3,3) te gaan (als je het als een
coŲrdinatenstelsel ziet) Dat zijn 6 nCr 3 = 20 manieren. Daar staat dus 20. |
||||
| 4. | In de gebruikelijk notatie: | ||||
 |
|||||
| De som van de
kolommen is achtereenvolgens: 8, 7, 6, 3, 2 De uitslag volgorde is dus A - B - C - D - E |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||