| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
| 1. |
Examenopgave Havo
Wiskunde B, 2018-II |
| |
|
|
|
| |
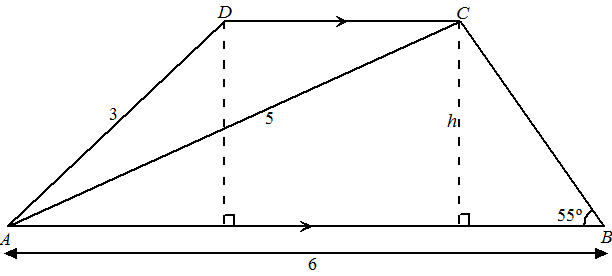
Een trapezium is een vierhoek met twee
evenwijdige zijden.
Gegeven is trapezium ABCD waarvan de zijden AB en
CD evenwijdig zijn.
Verder geldt: AB =
6, AC =
5, AD =
3, ∠B
=
55º
en ∠ACB
>
90º
.
De afstand tussen AB en CD, de hoogte
van het trapezium, is h.
Zie de figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Afgerond op twee decimalen is ∠BAC
gelijk aan 24,41º. |
| |
|
|
|
| |
a. |
Bereken ∠BAC algebraïsch en rond je
eindantwoord af op drie decimalen. |
| |
|
|
|
| |
De oppervlakte van het trapezium is te berekenen met
de volgende formule: O = 0,5h • (AB + CD) |
| |
|
|
|
| |
b. |
Bereken de oppervlakte van het trapezium met behulp
van deze formule. Rond je eindantwoord af op één decimaal.
|
| |
|
|
|
| 2. |
Examenopgave Havo
Wiskunde B, 2019-I |
| |
|
|
|
| |
Bij tennis is het soms moeilijk om te beoordelen
of een bal binnen of buiten de lijnen de grond raakt. Vaak wordt
met behulp van camera’s vastgesteld waar een bal de grond raakt.
Om een idee te krijgen hoe zo’n systeem werkt,
bekijken we een sterk vereenvoudigd tweedimensionaal model met
twee camera’s. In onderstaande figuur is een bovenaanzicht van
één helft van het rechthoekige speelveld weergegeven. Bovendien
zijn in deze figuur enkele maten gegeven. Alle maten zijn in
meters.
Ook zijn de witte lijnen op het speelveld aangegeven. In het
vervolg van deze opgave verwaarlozen we de breedte van deze
lijnen. De bal beschouwen we als een punt. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
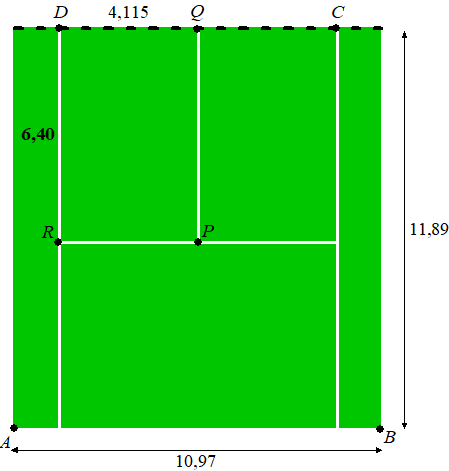
In deze figuur geldt:
-
de stippellijn door
CD
geeft de plaats van het net aan;
-
de lengte van de achterlijn
AB
is 10,97 m;
-
de afstand van de achterlijn tot aan het
net is 11,89 m;
- DQ
=
4,115
m en
DR
=
6,40
m;
- rechthoek
PQDR
is het servicevak, waarin de bal volgens de
regels van het spel na de eerste slag op de grond moet komen.
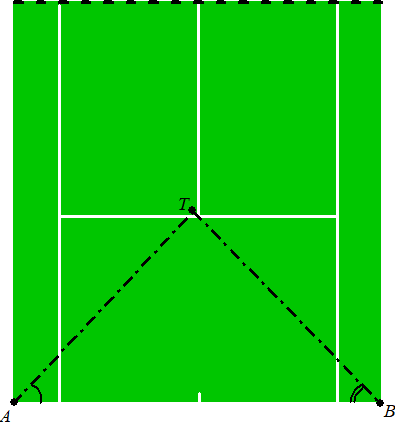
In de volgende figuur is hetzelfde speelveld nogmaals
weergegeven.
De camera’s zijn boven de punten
A
en
B
gemonteerd. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
In deze figuur geldt: |
| - |
A
is de positie van camera 1 en
B
is de positie van camera 2; |
| - |
het punt
T
is de plaats waar de bal na de eerste slag
op de grond komt; |
| - |
∠A
is de hoek ten opzichte van de
achterlijn waaronder camera 1 de bal waarneemt; |
| - |
∠B
is de hoek ten opzichte van de
achterlijn waaronder camera 2 de bal waarneemt; |
| - |
In de situatie zoals
weergeven in de figuur is de bal nog net in het servicevak
PQDR
op de grond gekomen. |
| |
|
|
|
| |
We
bekijken nu een andere situatie, waarbij ∠A
=
45,4°
en ∠B
=
44,2°
.
Onderzoek met behulp van een berekening of in
deze situatie de bal in rechthoek
PQDR
op de grond is gekomen. |
| |
|
|
|
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|