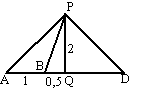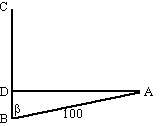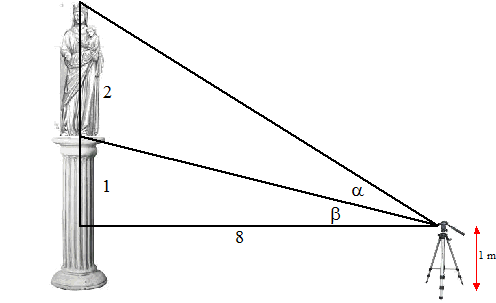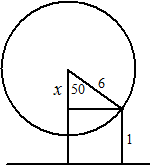|
|||||
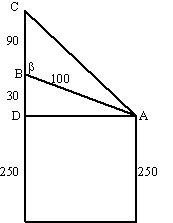
| 1. | zie de afbeelding
hiernaast. de motorboot vaart route ABC en legt in 4 uur 320 km af, dus x + y = 320 het schip vaart in 4 uur 128 km, dus AC = 128. de hoeken van driehoek ADC zijn 45º en 90º, dus geldt sin45º = AD/128 ⇒ AD = 128 • sin45º = 90, 51 cos45º = CD/128 ⇒ CD = 128 • cos45º = 90,51 Pythagoras in driehoek BDC: BD2 + DC2 = BC2 (90,51 + x)2 + 90,512 = y2 = (320 - x)2 90,512 + 2 • 90,51 • x + x2 + 90,512 = 3202 - 2 • 320 • x + x2 16384 + 181,02x + x2 = 102400 - 640x + x2 821,02x - 86016 = 0 x = 104,8 km |
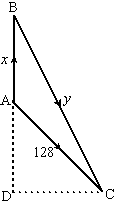 |
|||
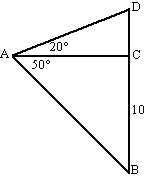
| 2. | tan50º = 10/AC
⇒ AC = 10/tan50º
= 8,39 cos20º = AC/AD = 8,39/AD ⇒ AD = 8,39/cos20º = 8,93 m |
 |
|||
| 3. | a. | AQ = 1,5 tanAPQ = 1,5/2 = 0,75 ⇒ ∠APQ = tan-10,75 = 36,87º dan is ∠APD = 73,74º |
|
||
| b. | BQ = 1/8AQ
= 0,1875 tanBPQ = 0,1875/2 = 0,0,09375 ⇒ ∠BPQ = tan-10,09375 = 5,356º dan is ∠BPQ = 2 • 5,356 = 10,712º |
||||
| c | Trek PQ helemaal door tot de
bodem van de put, en noem dat punt R. in driehoek RQP: tan5,356º = 1,5/PR PR = 1,5/tan5,356 = 16 dan is de punt 16 - 2 = 14 meter diep. |
||||
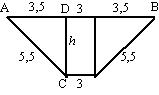
| 4. | a. | de weg is 10 m breed, dus AD =
3,5 het touw is 14 m lang, dus AC = 5,5 cosDAC = 3,5/5,5 = 0,6364 ⇒ ∠DAC = cos-10,6364 = 50,48º dan is a = 90 - 50,48 = 39,52º |
|
||
| b. | tan50,48º = h/3,5
⇒ h = 3,5 • tan50,48º = 4,24 m (het kan natuurlijk ook via Pythagoras in driehoek ADC) |
||||
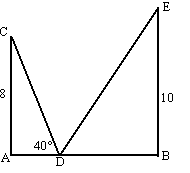
| 5. | tan40º = 8/AD
⇒ AD = 8/tan40º =
9,534 dan is BD = 12 - 9,534 = 2,466 tanα = 10/2,466 = 4,055 ⇒ α = tan-1 4,055 = 76.1º |
 |
|||
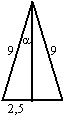
| 6. | zie de figuur
hiernaast. sinα = 2,5/9 = 0,278 ⇒ α = sin-10,278 = 16,1º de hoek tussen de benen is dan 2 • 16,1 = 32,2º |
|
|||
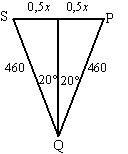
| 7. | a. | Als de hoek met de bodem 50º is, dan is
∠SQP = 40º zie de figuur hiernaast. sin20º = 0,5x/460 0,5x = 460 • sin20º = 157,3 x = 2 • 157,32 = 314,6 |
|
||
| b. | bekijk driehoek PTR tanTPR = 2,5/2 = 1,25 ⇒ ∠TPR = tan-11,25 = 51,3º de hoek waarover moet worden gedraaid is 90º - 51,3º = 39,7º |
||||
| van driehoek PQR in
de nieuwe situatie is PR2 = 2002 + 2502
=102500 dus PR = √102500 =
320,16 verder is PQ = 460 als Q recht boven R moet komen, dan is PRQ een rechte hoek. cosQPR = PR/PQ = 320,16/460 = 0,696 ⇒ ∠QPR = 45,9º dan is ∠QPS = 90 - 45,9 = 44,1º zie weer de figuur hierboven, de hoeken van 20º zijn nu gelijk aan 44,1/2 = 22,05º sin22,05º = 0,5x/460 0,5x = 460 • sin22,05º = 172,69 x = 2 • 172,69 = 345,4 |
|||||
| 8. |
Bekijk de driehoek op de grond en teken de
hoogtelijn. |
||||
| 9. | a. | AD2 + 302 = 1002
AD2 = 10000 - 900 = 9100 AD = √9100 = 95,4 AD2 + 1202 = AC2 9100 + 14400 = AC2 AC = √23500 = 153,3 |
|
||
| b. | zie de figuur hiernaast. cosβ = BD/100 ⇒ BD = 100 • cosβ omdat B al op hoogte 280 ligt, is de hoogte van A gelijk aan h = 280 + 100cosβ |
|
|||
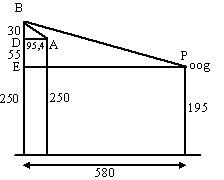
| c. | bij 250 m boven de grond was AD =
95,4 (vraag a) zie de figuur hiernaast. tan∠PBE = 580/85 = 6,82 ⇒ ∠PBE = 81,66º tan∠ABD = 95,4/30 = 3,18 ⇒ ∠ABD = 72,54º omdat ∠ABD < ∠PBE kan de speler WEL iets van het frame zien. |
 |
|||
| 10. | a. | De
oppervlakte van de rechthoek is 10 • 30 = 300 De twee halve cirkels zijn samen een hele cirkel met straal 5, en die heeft oppervlakte π • 52 = 25π Samen is dat 300 + 25π = 379 cm2 |
|||
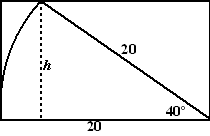
| b. | Het vooraanzicht
is als hiernaast. Daarin zie je dat sin40º = h/20 Dus h = 20 • sin40º = 12,9 Het doosje moet dus minstens 13 cm hoog zijn. |
 |
|||
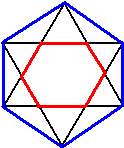
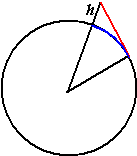
| 11. | noem de zwarte
lijnstukjes allemaal x, dan zijn de roden ook x kies een gelijkbenig driehoekje met twee zijden x en de derde zijde blauw (B) teken de hoogtelijn daarin. de tophoek is 120º dan geldt sin60º = 0,5B/x B = 2x • sin60º B = x√3 dus de verhouding is 1 : √3 |
|
|||
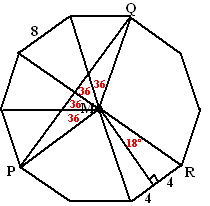
| 12. | a. | Bij een tienhoek zijn de hoeken
bij het middelpunt gelijk aan 36º. Dan geldt in de driehoek rechtsonder: sin18º = 4/MR MR = 4/sin18º = 12,944 |
 |
||
| b. | Bekijk driehoek MPQ. De hoek bij M is 4 • 36 = 144º teken de hoogtelijn van M op PQ. Dan heb je twee halve driehoeken met een rechte hoek. sin72º = x/12,944 x = 12,944 • sin72º = 12,31 Dan is PQ = 2 • 12,31 = 24,62 |
||||
| 13. |
|
||||
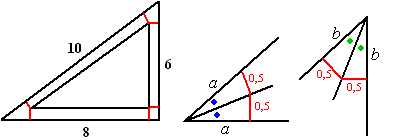
| Hierboven zie je de
baan van het middelpunt, met daarnaast de hoeken uitvergroot. De twee blauwe hoeken zijn samen een hoek van de grote driehoek en daarvoor geldt tanα = 6/8 dus α = 36,87º Dan is zo'n blauwe hoek 18,43º dan is tan18,43º = 0,5/a dus a = 0,5/tan18,43º = 1,5 De twee groene hoeken zijn samen 90 - 36,87º = 53,13º dus elke is 26,57º dan is tan(26,57º) = 0,5/b dus b = 0,5/tan(26,57º) = 1 De driehoek die
het middelpunt aflegt heeft dan zijden (8 - 0,5 - 1,5) en
(6 - 0,5 - 1) en (10 - 1,5 - 1) |
|||||
| 14. | a. | Noem de hoek bij het middelpunt
van de aarde a. Dan geldt: cosα = (6387/(h + 6378)) dus α = cos-1((6387/(h + 6378)) De blauwe afstand is dan R • α en dat geeft de gevraagde formule |
|
||
| b. | h = 0,1 geeft d = 6378 • cos-1(6378/6378,1) = 6378 • 0,005599 = 35,7 km | ||||
| c. | cosα =
(R/(R + h)) = 1 - 0,5α2
uit vraag a) 0,5α2 = 1 - R/(R + h) = (R + h)/(R + h) - R/(R + h) = h/(R + h) |
||||
|
|
|||||
|
|
|||||
| d. | h = 0,1 geeft
met de formule d = 35,71530951 en vraag c) leverde
d = 35,71526285 Dat scheelt 0,000047 kilometer en dat is 4,7 cm |
||||
| 15. |
|
||||
| tan(β)
= 1/8 ⇒
β = 7,13º tan(α + β) = 3/8 ⇒ α + β = 20,56º Dan is de kijkhoek 20,56 - 7,12 = 13,43º tan(β) = 1/7 ⇒ β = 8,13º tan(α + b) = 3/7 ⇒ α + β = 23,20º Dan is de kijkhoek 23,20 - 8,13 = 15,07º De hoek is dus 1,64º groter geworden. |
|||||
| 16. | cos50º = x/6
dus x = 6 • cos50º = 3,86 m De hoogte is dan 4,86 m. |
|
|||
| 17. | Noem de horizontale
afstand tot de toren in het tweede geval x, en de hoogte van de
toren h tan41 = h/x geeft h = xtan41 tan34 = h/(x + 100) geeft dan tan34 = xtan41/(x + 100) (x + 100)tan34 = xtan41 xtan34 + 100tan34 = xtan41 100tan34 = x(tan41 - tan34) 67,451 = x • 0,1948 x = 346,3 h = 301 meter |
||||
| 18. | sinβ • tanβ = b/a • b/c = b²/ac = (a² - c²)/ac = a/c - c/a dus antwoord d. | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||