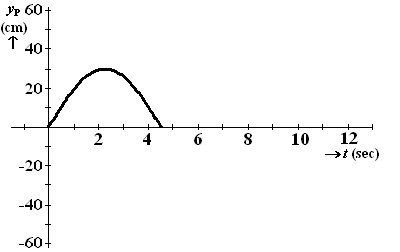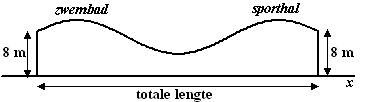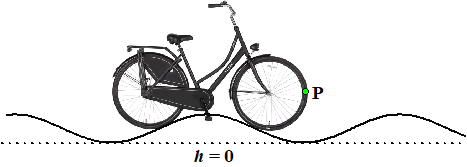|
© h.hofstede (hhofstede@hogeland.nl) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
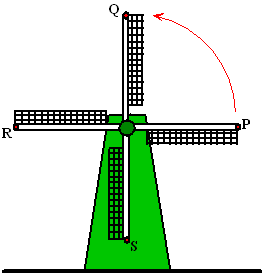
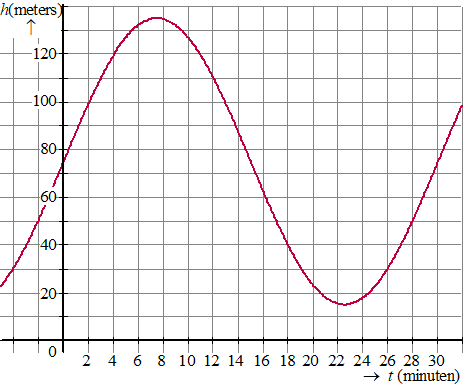
| 1. | Hiernaast zie je een
windmolen met de punten P, Q en R de uiteinden van de drie bladen. Kies
de oorsprong van een assenstelsel aan de voet van de molen. Dan ligt het punt waar de wieken aan de as zitten op een hoogte van 50 meter. De wieken hebben elk een lengte van 30 meter. Op tijdstip t = 0 staat wiek P op zijn laagste punt. In de foto hiernaast draait de molen tegen de klok in. Neem aan dat punt P ronddraait met een snelheid van 47 m/sec. Dan duurt één omwenteling ongeveer 4 seconden. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Toon dat aan. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Geef een formule voor de hoogte van punt P (HP) als functie van de tijd t (in sec). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Geef een formule voor de hoogte van punt Q (HQ) als functie van de tijd t (in sec). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d. | Bereken hoeveel procent van de tijd een punt zich op meer dan 70 m hoogte bevindt. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
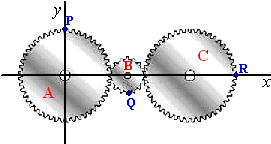
| 2. | Drie tandwielen (A, B
en C) hebben hun middelpunt vast op de x-as van een assenstelsel.
De wielen A en C hebben straal 16 cm, wiel B heeft straal 6 cm. Het middelpunt van A ligt in de oorsprong. A en C hebben elk 48 tanden, B heeft 18 tanden. P, Q en R zijn punten van de tandwielen A, B en C. Op t = 0 ligt P op de y-as, R op de x-as, en is Q het laagste punt van tandwiel B. De situatie op t = 0 is als hiernaast geschetst. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stel dat tandwiel A
precies 4 seconden doet over één omwenteling. Tandwiel A draait met de klok mee. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Geef een formule voor de x-coördinaat van punt P als functie van de tijd. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Geef een formule voor de x-coördinaat van punt R als functie van de tijd. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Geef een formule voor de y-coördinaat van punt Q als functie van de tijd. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | De hoogte van het
water in Helgoland is (o.a.) afhankelijk van de getijden. Een actuele voorspelling voor allerlei plaatsen kun je trouwens op deze site vinden. De havenmeester stelt voor 25 december 2011 de volgende vergelijking op: h(t) = 0,5 + 0,9sin0,52(t - 5) Daarin is t de tijd in uren vanaf 0:00 uur, en h de waterhoogte in meter. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Omdat jij natuurlijk weet dat het om de 12 uur eb is, kon je die 0,52 uit de formule zelf al wel voorspellen. Leg uit hoe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Wanneer zal het op 25 december 2011 hoogwater zijn in Helgoland? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Hoe lang zal het water op 25 december in Helgoland hoger dan 1,2 meter zijn? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | Bij de molen
hiernaast zijn de uiteinden van de wieken aangegeven met P, Q, R en S.
Voor de hoogte van punt P blijkt de volgende formule te gelden:
h(t) = 18 + 14sin(1/4πt) Hierin is h de hoogte in meters boven de grond en t de tijd in seconden. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Hoe kun je zien dat de hiernaast getekende situatie bij t = 0 hoort? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Hoe zou de formule veranderen als de molen de andere kant op zou draaien? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Geef een formule voor de hoogte van punt S als functie van de tijd. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | Gegeven zijn de volgende formules:
y1 = 3 - 2·sinx en y2 =
5·cosx - 1 en y3 = y1 +
y2 Geef een formule voor y3 van de vorm y3 = a + b·sin c(x - d) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
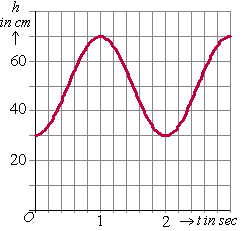
| 6. | Hiernaast zie je een grafiek van de hoogte boven de grond (h in cm) van een meisje dat op een schommel zit als functie van de tijd (t in seconden). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Geef een mogelijk functievoorschrift. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bepaal hoeveel procent van de tijd het meisje hoger dan 60 cm zit. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Bepaal de verticale snelheid van
het meisje op t = 0,6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | examenvraagstuk
VWO Wiskunde A, 1991. Bij het ontwerpen van gebouwen besteedt men aandacht aan de mogelijke bezonning. Daarbij gaat men uit van een altijd wolkeloze hemel. In deze opgave beperken we ons tot gebouwen met rechte verticale gevels die niet in de schaduw staan van andere objecten. Verder gaan we uit van een jaar met 365 dagen. In de volgende tabel is af te lezen hoeveel dagen elke kalendermaand telt. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
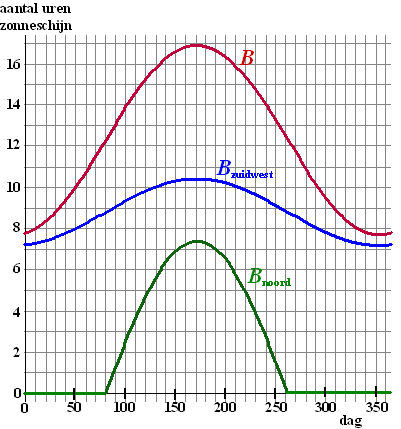
| In de figuur hieronder is het dagelijks
aantal uren zonneschijn B bij een altijd wolkeloze hemel uitgezet
tegen het nummer van de dag (n); hierbij geldt n = 1
voor 1 januari. Overeenkomstig zijn het dagelijks aantal bezonningsuren voor een zuidwestgevel (Bzuidwest) en dat voor een noordgevel (Bnoord) uitgezet. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uit deze figuur blijkt dat een noordgevel slechts een gedeelte van het jaar beschenen wordt. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Op 30 januari komt de zon op om 8 uur 27. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken met behulp van de formule het tijdstip waarop de zon op 30 januari onder gaat in minuten nauwkeurig. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Toon door berekening aan dat 12 april de eerste dag van het jaar is dat de zon langer dan 14 uur schijnt. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Neem aan dat de punten van de grafiek van Bzuidwest op een sinusoïde liggen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Stel een voorschrift op voor deze sinusoïde met behulp van de figuur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Gevels aan weerszijden van een rechthoekig gebouw kunnen niet tegelijkertijd door de zon beschenen worden | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d. | Teken in de figuur hierboven de grafiek voor het dagelijks aantal bezonningsuren voor een zuidgevel. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | examenvraagstuk HAVO Wiskunde B, 2004. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
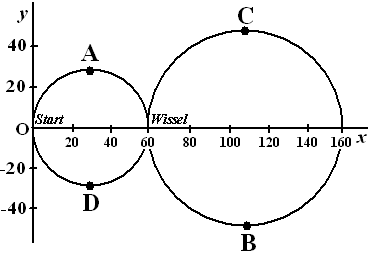
| Jules heeft voor zijn verjaardag een elektrische trein gekregen. Op een houten plaat bevestigt hij een treinbaan. Met behulp van zijn computer tekent Jules het model van de treinbaan in een assenstelsel; zie de volgende figuur. Het model van de treinbaan bestaat uit cirkelvormige delen met stralen van 30 cm en 50 cm. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een trein die met een constante snelheid
rijdt, legt in 24 seconden de volledige baan af volgens de route Start
→ A →
Wissel → B →
C → Wissel →
D → Start. De voorkant van de trein wordt in het computermodel voorgesteld door een punt P met coördinaten (xP , yP). De waarden van xP en yP hangen af van de tijd t. Hierbij is t de tijd in seconden vanaf het moment dat het punt P het startpunt O(0,0) in de figuur hierboven passeert. In de volgende grafiek is yP uitgezet tegen de tijd t waarbij t tussen 0 en 4,5 ligt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Geef bij deze grafiek een bijbehorende formule. Licht je antwoord toe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Teken voor de eerste 12 seconden na de start de grafiek van yP als functie van de tijd t. Licht je werkwijze toe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
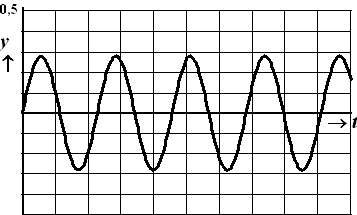
| 9. | examenvraagstuk
HAVO Wiskunde B, 2006. Bij een stemvork die in trilling gebracht wordt, maken de uiteinden zeer snelle heen en weergaande bewegingen rond de evenwichtsstand. De afstand van een uiteinde tot deze evenwichtsstand heet de uitwijking. De grafiek van de uitwijking y, afhankelijk van de tijd t, is een sinusoïde. De trilling van de stemvork brengt de lucht in trilling. Dit horen wij als geluid. Van twee stemvorken A en B krijgt men met behulp van een oscilloscoop de grafiek van het trillingspatroon. In de figuur rechts staat de grafiek voor stemvork A. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bij deze grafiek hoort de
formule: Stemvork A: y = 0,28 • sin(0,88πt) Hierin is t de tijd in milliseconden (1 milliseconde is 0,001 seconde) en y de uitwijking in millimeters. De trilling van stemvork A begint op t = 0. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken het aantal trillingen per seconde voor stemvork A. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als de frequentie groter wordt
wordt de toon hoger. Als de amplitude (maximale uitwijking) groter wordt, wordt het geluid harder. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor stemvork B geldt de
formule: Stemvork B: y = 0,14 • sin(0,88π(t
- 0,5)) De beide stemvorken klinken dus even hoog, maar stemvork B klinkt
zachter dan stemvork A. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Stel een mogelijke formule op voor de trilling van stemvork C. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. | examenvraagstuk HAVO Wiskunde B, 2008. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Op de foto zie je een zwembad met sporthal, samen onder één golvend dak. Het golvende dak bereikt boven het zwembad dezelfde hoogte als boven de sporthal. In de figuur hieronder is een schematisch vooraanzicht getekend. In dit vooraanzicht heeft de rand van het dak de vorm van een sinusoïde met als formule |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De hoogte h en de lengte x zijn allebei in meter. De lengte x wordt van links naar rechts over de grond gemeten langs de voorkant van het gebouw, vanaf een punt O dat links van de linkerkant van de voorgevel van het gebouw ligt. Aan beide uiteinden van het gebouw is het dak 8 meter hoog. Zie onderstaande figuur | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken exact de minimale en de maximale hoogte van het dak. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken de totale lengte van het gebouw in gehele meters nauwkeurig. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
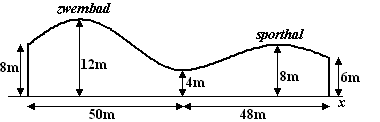
| Voordat het zwembad met sporthal werd gebouwd, heeft een architect een ontwerp gemaakt van het gebouw. In het eerste ontwerp dat de architect had gemaakt, was het dak boven het zwembad hoger dan het dak boven de sporthal. Ook de lengte van de voorkant van het gebouw in dit eerste ontwerp was anders dan die van het uiteindelijke gebouw. In de volgende figuur staan de afmetingen van het gebouw volgens het eerste ontwerp. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het gedeelte van het dak dat boven het zwembad ligt, heeft in het vooraanzicht de vorm van een sinusoïde. Dit geldt ook voor het gedeelte van het dak boven de sporthal. De twee sinusoïdes gaan vloeiend in elkaar over op de grens tussen zwembad en sporthal op een hoogte van 4 meter. Op die grens is de hoogte van het dak minimaal. Boven de sporthal heeft het dak een maximale hoogte van 8 meter. Zie de figuur. Met behulp van deze gegevens kun je een formule opstellen die hoort bij het vooraanzicht van het gedeelte van het dak boven de sporthal volgens het eerste ontwerp | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Stel deze formule op. Je mag zelf de oorsprong kiezen. Licht je werkwijze toe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. | examenvraagstuk VWO Wiskunde B,
1989. Voor elke p ∈ N+ is gegeven de functie fp : x → p - 1 + cospx met domein [0, 2π]. Ten opzichte van een rechthoekig assenstelsel Oxy is Fp de grafiek van fp. Onderzoek voor welke p de lijn y = 1/2p en Fp minstens vier punten gemeenschappelijk hebben. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
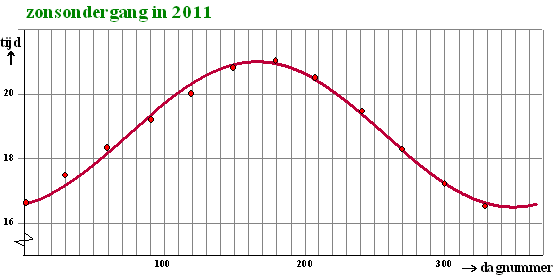
| 12. | In de volgende tabel staan de tijden van zonsopkomst en zonsondergang in 2011. (de tijden zijn gegeven in Midden-Europese-Tijd (MET), dus van april tot en met oktober was het vanwege de zomertijd op onze klokken een uur later) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De grafiek voor zonsondergang staat hieronder en is, zoals je ziet, aardig door een sinusgrafiek te benaderen.. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Geef een sinusformule die de grafiek hierboven beschrijft. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het tijdstip van zonsopgang is ook aardig door een sinusformule te beschrijven. De vroegste zonsopgang was op 30 juni, en dat was om 4:19. De laatste zonsopgang was op 30 december, en dat was om 8:48. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Geef een sinusformule voor het tijdstip van zonsopgang. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De daglengte is gelijk aan het verschil tussen zonsopgang en zonsondergang. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Plot de grafiek van de daglengte, en schrijf vervolgens de daglengte D als D = a + bsinc(x + d) waarbij x het dagnummer is. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
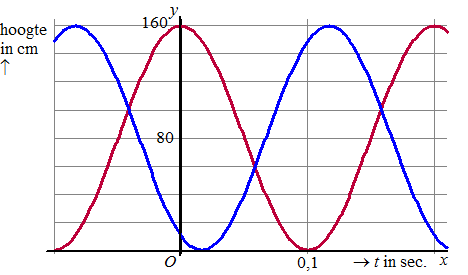
| 13. | Bij een grote draaiende
ventilator kiezen we een assenstelsel met de x-as en de y-as
zoals hiernaast aangegeven. De tekening hiernaast geeft de toestand op t = 0. De ventilator draait tegen de klok in. Hieronder zie je twee grafieken van de hoogte y van twee uiteinden van bladen van de ventilator. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Leg uit welke grafiek bij welk punt van de ventilator hoort. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Hoeveel omwentelingen per minuut maakt de ventilator? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Geef een formule voor de hoogte (in cm) van het onderste punt van de ventilator op de begintekening als functie van de tijd in seconden. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14. | examenvraagstuk HAVO wiskunde B, 2016-I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Van de maan is ook bij een wolkeloze hemel niet altijd een even groot gedeelte zichtbaar. Het percentage van de maan dat zichtbaar is, verloopt bij benadering periodiek.
P = 50 + 50sin (0,212769t - 1,042563) Hierin is P het percentage van de maan dat zichtbaar is en t is de tijd in dagen met t = 0 op 1 januari 2017 om 0:00 uur. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken de periode van P in hele minuten nauwkeurig. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De vorm van het zichtbare gedeelte van de maan wordt de schijngestalte van de maan genoemd. Vier speciale schijngestalten zijn nieuwe maan, eerste kwartier, volle maan en laatste kwartier. Zie de figuur, waarin ze op volgorde staan afgebeeld, elk met het bijbehorende percentage van de maan dat zichtbaar is. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De volgorde waarin deze schijngestalten voorkomen, is dus altijd: eerst nieuwe maan, dan eerste kwartier, dan volle maan en daarna laatste kwartier. Daarna volgt opnieuw nieuwe maan, enzovoort. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Onderzoek met behulp van de formule voor P tussen welke twee opeenvolgende schijngestalten de maan zich op 22 februari 2017 zal bevinden | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15. | examenopgave HAVO wiskunde B, 2016-II | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
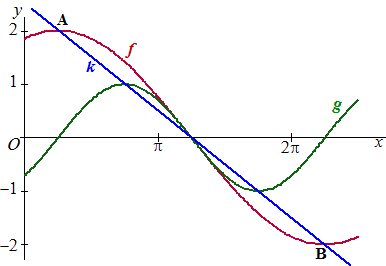
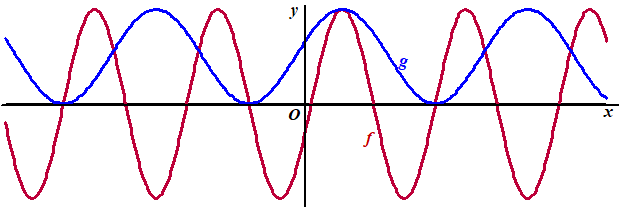
|
Op het domein [0, 5/2π]
zijn gegeven de functies: de f(x) = 2cos(1/2x - 1/8π) en g(x) = sin(x - 1/4π) De lijn k die door de toppen van de grafiek van f gaat, gaat ook door de toppen van de grafiek van g. Zie de figuur. Toon dat aan. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16. | Examenopgave VWO Wiskunde A, 2017-I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Op de foto’s zie je het Zentrum Paul Klee in Zwitserland. Het gebouw heeft een bijzondere vorm: het bestaat uit drie afdelingen met daaroverheen een golvend dak. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
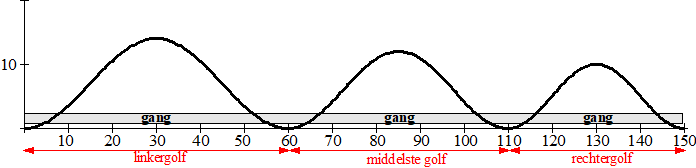
| De drie afdelingen zijn verbonden door een lange gang. In onderstaande figuur zie je een schematische doorsnede van het gebouw en de lange gang. In deze figuur is duidelijk te zien dat het dak bestaat uit drie golven met verschillende periodes. Ook de hoogtes zijn verschillend. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Elke golf begint en eindigt op een laagste punt. Voor de linker golf in de figuur kan men de volgende formule opstellen: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hierin is h de hoogte van de golf boven het laagste punt in meter en x de horizontale afstand in meter vanaf het beginpunt van deze golf. De vloer van de gang bevindt zich 1 meter boven het laagste punt van de golven. De gang zelf is 3,5 meter hoog. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken de lengte van het gedeelte van de gang dat zich geheel onder het linker dak, dus onder de linker golf, bevindt in cm nauwkeurig. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
De golf die hoort bij het middelste dak is 51 meter lang
en 12,5 meter hoog. Hier hoort een formule bij van de vorm h = a + asin (c(x + d)) met h de hoogte van de golf in meter boven het laagste punt en x de horizontale afstand in meter vanaf het beginpunt van de linker golf. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken de waarden van a, c en d in deze formule. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
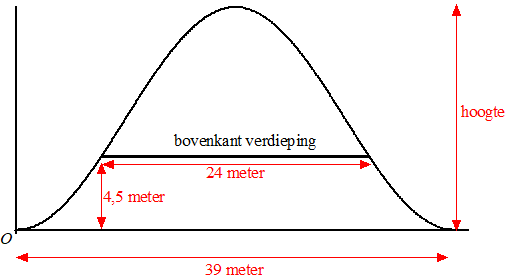
| We kijken nu naar het rechter dak. Om de afmetingen hiervan te berekenen, kan de architect bijvoorbeeld als volgt te werk gaan. Hij gaat voor het dak uit van een sinusoïde met een periode van 39 meter. Verder wil hij dat onder het dak een benedenverdieping past van 24 meter breed en 4,5 meter hoog. In onderstaande figuur is de doorsnede getekend die bij deze situatie hoort. De golf begint linksonder in het punt met coördinaten (0,0). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Bereken, welke hoogte de architect nu minimaal moet nemen voor de golf die hoort bij het dak in deze situatie. Geef je antwoord in dm nauwkeurig. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17. | examenopgave HAVO wiskunde B, 2018-I | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
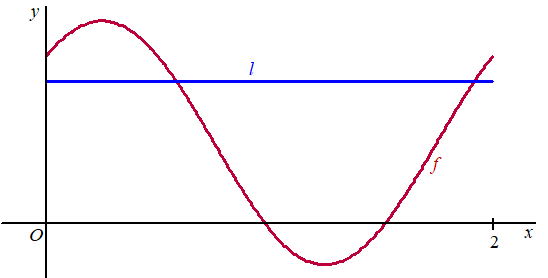
Op het domein [0, 2π] is de functie f gegeven door: f(x) = 2 + 3sin(π(x + 1/4))Verder is de lijn l gegeven door de vergelijking y = 7/2 Zie figuur. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Op het gegeven domein snijden l en de grafiek van f elkaar in twee punten. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken exact de x-coördinaten van deze punten. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Een functie
g
heeft een functievoorschrift van de vorm:
g(x) = p + q • cos(r(x
-
s)) Er geldt: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De periode van g is 4. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | Het hoogste punt van de grafiek van g valt samen met het hoogste punt van de grafiek van f. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De amplitude van de grafiek van g is twee keer zo groot als de amplitude van de grafiek van f. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken mogelijke exacte waarden van p, q, r en s. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18. | examenopgave VWO wiskunde A, 2018-I. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Op de foto zie je een doorgezaagde boomstam.
Hierin zijn zogenaamde jaarringen te
zien. Deze ontstaan doordat de boom in de zomer snel groeit: dan
wordt er licht gekleurd hout gevormd. In deze opgave kijken we eerst naar de groeisnelheid van de diameter ( G) van een grove den. Omdat een boom afwisselend snel en langzaam groeit, kun je deze groeisnelheid modelleren met behulp van sinusoïden. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor de groeisnelheid van de diameter van een grove den gelden de volgende eigenschappen: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | de groeisnelheid is drie maanden na het ontkiemen van het zaadje maximaal; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | de groeisnelheid is negen maanden na het ontkiemen minimaal; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | dit patroon herhaalt zich elk jaar; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | de maximale groeisnelheid is 2,1 cm per jaar; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | de minimale groeisnelheid is 0,3 cm per jaar. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voor de groeisnelheid van de grove den kun je op basis van deze eigenschappen een formule opstellen van de vorm G = a + bsin(c(t - d)) . Hierin is G de groeisnelheid in cm per jaar en t de tijd in jaren na het ontkiemen.Bereken de waarden van a, b, c en d in deze formule. Licht je antwoord toe. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19. | examenopgave HAVO wiskunde B, 2019-II | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
De functie
f
wordt gegeven
door f
(x)
=
-1
+ sin(2x
-
1/6π)
. De grafiek van f is in de volgende figuur weergegeven. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Er zijn vier waarden van x in het interval 0 ≤ x ≤ 2π waarvoor geldt f(x) = -1/2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken exact deze vier waarden van x. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
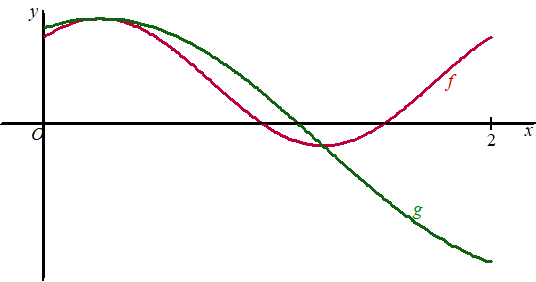
| We bekijken nu de functie g. Deze heeft de volgende eigenschappen: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De grafiek van g is een sinusoïde. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De periode van de grafiek van g is drie keer zo klein is als de periode van de grafiek van f. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De amplitude van de grafiek van g is vier keer zo klein als de amplitude van de grafiek van f. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | Een laagste punt van de grafiek van g valt samen met het snijpunt van de grafiek van f met de y-as. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Functie g heeft een functievoorschrift van de volgende vorm: g(x) = d + a · cos(bx)Hierin zijn a, b en d getallen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken exact voor elk van deze drie getallen een mogelijke waarde. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20. | examenopgave VWO wiskunde A, 2019-I. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Langs het Zandpad in Utrecht staat een hek dat bestaat uit twee sinusoïden, die elkaar raken. Zie de foto. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In de figuur hieronder zijn de twee sinusoïden in het hek schematisch weergegeven. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
De formule die bij de onderste sinusoïde hoort,
luidt: Sonderste = 100 + 50sin(1/3πx) Hierbij is Sonderste de hoogte in centimeters en x de afstand tot het beginpunt op de evenwichtsstand in meters.De toppen van de onderste sinusoïde liggen op de
evenwichtsstand van de bovenste sinusoïde. De amplitudes van beide
sinusoïden zijn gelijk. Geef de formule voor de bovenste sinusoïde en licht toe hoe je je antwoord gevonden hebt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
We
bekijken in deze opgave de hoogte van een punt P van het wiel van een
fiets die met constante snelheid rijdt. De diameter van het wiel is
71,12 cm. P(t) = 35,56 + 35,56•sin(1,60•t - 3,14) Daarin is P gegeven in cm en t in seconden |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken hoe snel de fiets rijdt. Rond je antwoord af op een geheel aantal km/uur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Geef de betekenis van het getal 3,14 uit de formule. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Natuurlijk
is het veel leuker als je de fiets over een hobbelweg laat rijden. We rijden met de fiets over een weg waarvan de hoogte een sinusgrafiek is. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voor de
hoogte (H im cm) van de weg vanaf de lijn h = 0 op de plaats van
punt P blijkt te gelden:
H(t) = 13,2 + 13.2•sin(1,60•t + 0,73) Voor de hoogte h van punt P (vanaf de lijn h = 0) geldt dan: h(t) = P(t) + H(t) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Geef een formule voor h(t) in de vorm h(t ) = a + b•sin(c•t + d) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22. | examenvraagstuk
HAVO Wiskunde B, 2021-I. De functie f wordt gegeven door |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
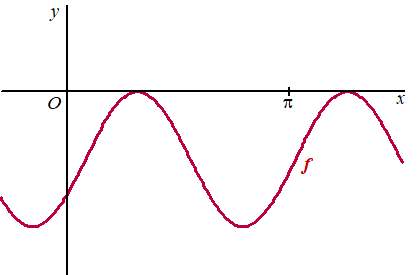
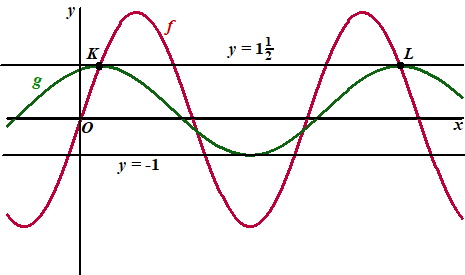
| In onderstaande
figuur is de grafiek van f getekend en ook de lijn met
vergelijking y = 11/2.
Deze lijn heeft oneindig veel snijpunten met de grafiek van f.
Het eerste snijpunt rechts van de y-as is K, het
vierde is L. In de figuur is met een groene lijn nog een sinusoïde weergegeven. Voor deze sinusoïde geldt: - De eerste top rechts van de y-as valt samen met K. - De derde top rechts van de y-as valt samen met L. - De sinusoïde raakt de lijn met vergelijking y = -1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De functie g
die bij de groene grafiek hoort, heeft een functievoorschrift
van de volgende vorm: g(x) = a cos(b(x - c)) + d Hierin zijn a, b, c en d getallen. Bereken exact voor elk van deze vier getallen een mogelijke waarde. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
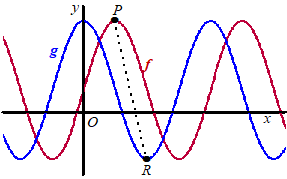
| 23. | Examenvraagstuk HAVO Wiskunde B, 2022-II | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De functies f en
g worden gegeven door: f(x) = 1 + 3sin(2x) g(x) = 1 + 3cos(2x) Het punt P is de eerste top van de grafiek van f rechts van de y-as en het punt R is de eerste top van de grafiek van g rechts van de y-as. Zie de figuur hiernaast, waarin ook het lijnstuk PR getekend is |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken algebraïsch de lengte van lijnstuk PR. Geef je eindantwoord in twee decimalen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
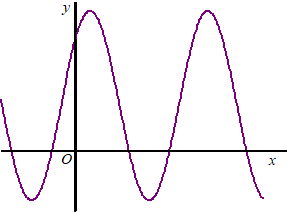
| De grafiek van
de somfunctie h(x) = f(x) + g(x)
blijkt ook een sinusoïde te zijn. Zie de figuur hiernaast. Het functievoorschrift van h is te schrijven als: h(x) = p + q • cos(r(x - s)) |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken mogelijke waarden van p, q, r en s. Geef je eindantwoorden, indien nodig, in twee decimalen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24. | Examenvraagstuk VWO Wiskunde
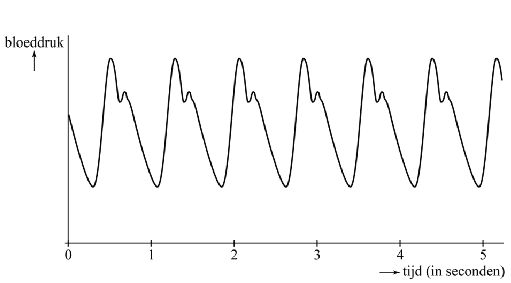
A, 2022-III Het hart pompt bloed door het menselijk lichaam. Als het hart samentrekt, wordt bloed in de bloedvaten gepompt, met als gevolg dat deze onder druk komen te staan. Als het hart zich weer ontspant, neemt de druk in de bloedvaten weer af. Dit proces herhaalt zich voortdurend en het aantal keren per minuut dat dit gebeurt, noemen we de hartslag. Tijdens dit proces neemt de druk in de bloedvaten dus steeds toe en weer af. De hoogste druk wordt de bovendruk genoemd en de laagste druk noemt men de onderdruk. Van een bepaalde persoon is in de volgende figuur de bloeddruk uitgezet tegen de tijd. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bepaal met behulp van deze figuur de hartslag van deze persoon. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als model van
de bloeddruk wordt vaak een sinusoïde van de vorm P = a
+ bsin(c • t) gebruikt. Hierin is P de
bloeddruk, t de tijd in seconden en zijn a b,
en c constanten. Deze constanten zijn afhankelijk van de
hartslag en worden zo gekozen dat maximum en minimum van de
sinusoïde overeenkomen met bovendruk en onderdruk. Een tweede persoon heeft een hartslag van 66 slagen per minuut. Zijn bovendruk is 124 en zijn onderdruk is 82. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Stel een formule voor P op van de bloeddruk van deze persoon, horend bij het model van de sinusoïde. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
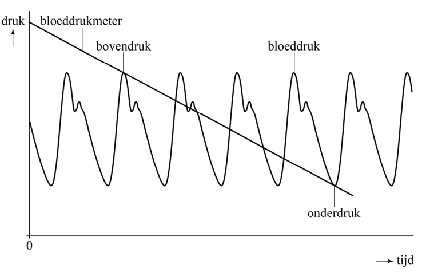
| Bloeddruk meten wordt meestal gedaan met de methode van Riva-Rocci, genoemd naar de Italiaanse uitvinder ervan. Die werkt als volgt: met een opblaasbare band om de bovenarm wordt de polsslagader afgekneld, zodat er geen bloed meer doorheen stroomt. Daarna laat men langzaam de lucht uit de band lopen, totdat er voor het eerst weer een bloedstroming waarneembaar is. De bijbehorende druk is de bovendruk. Daarna laat men de band nog verder leeglopen, totdat de bloedstroming niet meer waarneembaar is. De druk die daarbij hoort is de onderdruk. In onderstaande figuur staat een schets die bij deze methode past. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In deze figuur
gaat de lijn van de bloeddrukmeter precies door twee toppen van de
bloeddruk. In werkelijkheid is dit meestal niet zo, omdat het
verloop van deze lijn afhangt van hoe ver de band opgeblazen wordt
en hoe snel deze leegloopt. Daarom is een dergelijke bloeddrukmeting
nooit helemaal nauwkeurig. Boven- en onderdruk (of eigenlijk
benaderingen daarvan) worden gevonden door te bepalen waar de twee
grafieken elkaar voor het eerst en voor het laatst snijden. Van een patiënt kan de bloeddruk benaderd worden met de formule: P = 110 + 23sin(2πt) (met P in mmHg en t in seconden) Bij een bloeddrukmeting volgens de methode van Riva-Rocci pompt een verpleegkundige een bloeddrukmeter op tot een waarde van 170 mmHg. Daarna laat hij, vanaf t = 0 , de druk gelijkmatig afnemen met 10 mmHg per seconde. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Bereken welke bovendruk en onderdruk de verpleegkundige rapporteert. Geef je antwoord in gehele getallen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25. | Examenvraagstuk VWO Wiskunde A, 2022-II | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
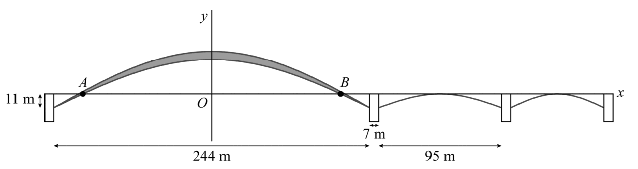
| De Waalbrug is
een verkeersbrug die Nijmegen en Lent met elkaar verbindt. In onderstaande figuur is een schematische tekening van de Waalbrug weergegeven. Hierin zijn de rechthoekjes de pijlers van de brug en is de horizontale lijn het wegdek. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De Waalbrug
heeft vijf bogen, waarvan er vier zich geheel onder het wegdek
bevinden. De middelste boog, de zogenaamde hoofdboog, heeft een
boven- en een onderrand. De onderrand komt tussen de punten A
en B boven het wegdek uit. In de figuur is het wegdek als
x-as genomen en gaat de y-as door de top van de
hoofdboog. Voor de onderrand van de hoofdboog kan de volgende
formule worden opgesteld: y = -11 + 38,6 • sin(π/244 • (x + 122)) Hierin zijn x en y in meters. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken de afstand van het wegdek tussen de punten A en B. Geef je antwoord in gehele meters. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De formule van de bovenrand wordt verkregen door de formule in verticale richting te herschalen met factor 1,17 en vervolgens met 1,87 omhoog te schuiven. Met behulp van de formules voor de boven- en de onderrand kan de verticale afstand tussen de boven- en de onderrand van de hoofdboog worden berekend. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken de verticale afstand tussen de boven- en de onderrand bij het hoogste punt van de hoofdboog. Geef je antwoord in meters en in één decimaal. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De gehele lengte van het wegdek dat hoort bij de hoofdboog – het stuk tussen de twee middelste pijlers – bedraagt 244 meter. Zie onderstaande figuur. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Net als de
hoofdboog bestaan de andere vier bogen uit een halve periode van een
sinusfunctie. Voor de boog direct rechts van de hoofdboog kan een
formule worden opgesteld van de vorm y
= a + bsin(c(x -
d)) Hiervoor zijn de volgende gegevens van belang, zie de figuur: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De pijlers zijn 7 meter breed. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | De boog begint direct naast de pijler op 11 meter onder het wegdek. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | Het hoogste punt van de boog raakt het wegdek. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| - | Het wegdek dat boven de boog ligt, heeft een lengte van 95 m. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Stel de formule op voor de boog direct rechts van de hoofdboog. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26. |
Gegeven is de functie
f(x) = 3sin(1/2x
-
1/12π) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
De functie g heeft ook een sinusvormige grafiek De minima van g vallen steeds samen met nulpunten van f. Het eerste maximum van g rechts van de y-as valt samen met het eerste maximum van f. Zie de figuur. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stel een functievoorschrift op voor functie g. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27. | Examenvraagstuk HAVO
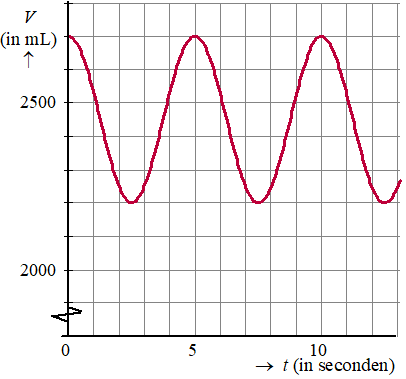
Wiskunde-B 2023-I In deze opgave bekijken we het longvolume. Dit is de hoeveelheid lucht in de longen van de mens. In onderstaande figuur is voor een bepaalde persoon in rust weergegeven hoe dit longvolume V afhangt van de tijd. Hierbij is V in mL en t de tijd in seconden. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Deze
grafiek is te beschrijven met een formule van de volgende vorm:
V = p + q · cos(rt) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken de waarden van p, q en r. Geef niet-gehele waarden in je eindantwoord in twee decimalen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als een persoon zich inspant, zal hij sneller gaan ademen. Ook ademt hij elke keer méér lucht in dan wanneer hij in rust is. Voor iemand die zich inspant, geldt: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
V = 2500 + 1200 · sin(4,19(t - 0,37)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hierin is
V het longvolume in mL en t de tijd in seconden.
De hoeveelheid lucht die deze persoon elke keer inademt, is gelijk aan het verschil tussen het maximum en het minimum van V. Gedurende één minuut ademt deze persoon meerdere keren in. In totaal ademt hij dan bijna 100 liter lucht in. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken hoeveel liter lucht deze persoon per minuut inademt. Geef je eindantwoord als geheel getal. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28. | Examenvraagstuk VWO Wiskunde
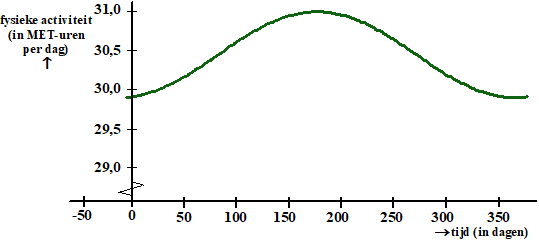
A, 2023-I. Na de feestdagen blijken Amerikanen gemiddeld zwaarder dan daarvoor. Dat zou mede veroorzaakt kunnen worden door de geringe hoeveelheid lichaamsbeweging in die periode. In onderstaande figuur is voor de groep onderzochte Amerikanen het verband geschetst tussen de totale fysieke activiteit per dag en de tijd. Hierbij komt t = 0 overeen met 1 januari. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De totale fysieke activiteit per dag varieert jaarlijks van minimaal 29,4 MET-uren per dag tot 30,5 MET-uren per dag. Op 21 december, de kortste dag, is de totale fysieke activiteit per dag minimaal. De totale fysieke activiteit wordt gemodelleerd met een formule van de vorm: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
F = a + bsin(c(t - d)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hierin is F de totale fysieke activiteit in MET-uren per dag en is t de tijd in dagen met t = 0 op 1 januari. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken de waarden van a, b, c en d. Geef a en b in twee decimalen, c in vijf decimalen en d in gehelen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
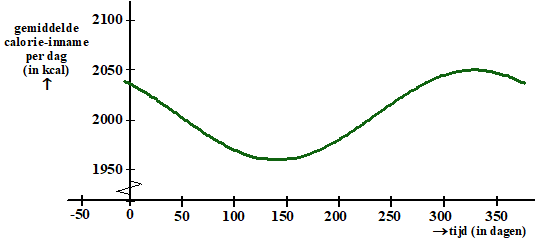
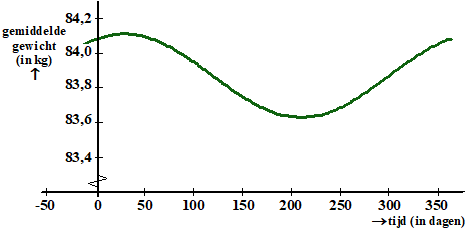
| Men heeft ook bijgehouden hoeveel calorieën de deelnemers gemiddeld per dag gedurende het jaar binnenkregen en hoe het gemiddelde gewicht van de deelnemers gedurende het jaar varieerde. Zie de volgende twee figuren. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De gemiddelde
calorie-inname wordt gemodelleerd met de formule: C(t) = 2005 + 45sin(0,0172t + 2,3756) Hierin is C de gemiddelde calorie-inname in kcal per dag en is t weer de tijd in dagen met t = 0 op 1 januari. Het gemiddelde gewicht wordt gemodelleerd met de formule: G(t) = 83,87 + 0,24sin(0,0172t + 1,1017) Hierin is G het gemiddelde gewicht in kg en is t weer de tijd in dagen met t = 0 op 1 januari. Het grootste verschil in gemiddeld gewicht in een jaar is procentueel gezien kleiner dan het grootste verschil in gemiddelde calorie-inname in een jaar. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Toon dit aan met behulp van de formules. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het gemiddelde gewicht is later maximaal dan de gemiddelde calorie-inname. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Bereken hoeveel dagen later dit volgens de formules is. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29. | De London Eye
is een reuzenrad in Londen. Zie de foto. De London Eye heeft 32 gondels, waarin de bezoekers plaatsnemen. Eén rondgang van een gondel duurt precies 30 minuten. De grafiek in de figuur hoort bij de hoogte van een van de gondels. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bij deze grafiek hoort de formule h(t) = 75 + 60sin(0,209t). Hierbij is h de hoogte van de gondel boven de grond in meters en t de tijd in minuten met t = 0 om 11.00 uur ’s ochtends. Deze grafiek hoort echter niet bij de gondel die zich om 11.00 uur bij het instapplatform in het laagste punt bevindt. De grafiek van de gondel die zich om 11.00 uur in het laagste punt bevindt, heeft een formule van de vorm h(t) = 75 + 60 sin(0,209(t - d)) . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. | Bereken een mogelijke waarde van d. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De gondels draaien met een dusdanig lage constante snelheid dat bij het in- en uitstappen het reuzenrad niet hoeft te worden stilgezet. Deze constante snelheid is even groot als de maximale snelheid waarmee h toeneemt of afneemt. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b. | Bereken deze constante snelheid in km/uur. Geef je antwoord in twee decimalen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hoe hoger je in het reuzenrad komt, hoe verder je kunt kijken. Met de formule | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| waarbij a
de maximale kijkafstand in meters is en h de hoogte boven de
grond in meters, kun je benaderen hoe ver je kunt kijken vanaf een
bepaalde hoogte boven de grond. Windsor Castle ligt hemelsbreed 40 kilometer van de London Eye vandaan. Op een heldere dag kun je vanuit de London Eye Windsor Castle zien liggen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c. | Bereken hoelang je per rondgang vanuit de London Eye op een heldere dag Windsor Castle kunt zien. Geef je antwoord in gehele minuten. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
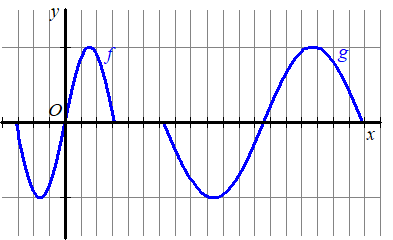
| 30. | In de figuur zie je
de grafieken van twee functies f en g. Welk verband geldt er tussen de functievoor schriften ? a. g(x) = f(2x + 4) b. g(x) = f(0,5x - 2) c. g(x) = f(2x + 2) d. g(x) = f (0,5x + 2) e. g(x) = f(2x - 2) |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© h.hofstede (hhofstede@hogeland.nl) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||