|
|||||||||
| 1. | a. | de lengte is 30 m dus
het uiteinde beschrijft een cirkel met straal 30 m de omtrek daarvan is 2π 30 = 188,5 m de snelheid is 47 m/sec, dus 188,5 m duurt 188,5/47 = 4,01 seconden |
|||||||
| b. | evenwichtslijn 50 amplitude 30 periode 4 sec. dus in de formule staat 2π/4 = π/2 op t = 0 het laagste punt, dus we nemen een cosinusgrafiek die is gespiegeld in de x-as. Dat geeft P(t) = 50 - 30 cos(π/2 t) |
||||||||
| c. | punt Q was 1/3
periode eerder dan P in het laagste punt. je krijgt de grafiek van Q door die van P 1/3 periode (is 4/3 sec) naar links te schuiven Dat geeft P(t) = 50 - 30 cos(π/2 (t + 4/3)) |
||||||||
| d. | 50 - 30 cos(π/2
t) = 70 plot Y1 = 50 - 30 cos(p X/2) en Y2 = 70 intersect geeft t = 1,465 en t = 2,535 daartussen ligt 1,07 seconden en dat is 1,07/4 100% = 27% van de periode |
||||||||
| 2. | a. | evenwichtslijn 0 amplitude 16 periode 4 seconden, dus in de formule staat 2π/4 = π/2 beginpunt x = 0 op t = 0 en die neemt toe, dus we nemen een gewone sinus: P(t) = 16 sin(π/2t) |
|||||||
| b. | evenveel tanden als A, dus de
periode is weer 4 seconden. evenwichtslijn 16 + 6 + 6 + 16 = 40 amplitude 16 beginpunt maximaal op t = 0 dus we nemen een cosinus: R(t) = 40 + 16 cos (π/2 t) |
||||||||
| c. | 48 tanden duurt 4 seconden dan duurt 18 tanden 18/48 4 = 1,5 seconde, dus de periode van B is 1,5 dan staat in de formule 2π/1,5 = 4/3π evenwichtslijn is 0 amplitude is 6 op t = 0 het laagste punt dus we nemen een cosinus die is gespiegeld. Q(t) = -6 cos(4/3πt) |
||||||||
| 3. | a. | als de periode 12 is, dan staat in de formule 2π/12 = 0,52 | |||||||
| b. | het beginpunt is bij
t = 5, dus het maximum is een kwart periode verder, dus 3 uur na
t = 5 dat is op t = 8 (en 12 uur later om t = 20 uur weer) |
||||||||
| c. | 1,2 = 0,5 +
0,9sin0,52(t - 5) plot Y1 = 0,5 + 0,9sin0,52(X - 5) en Y2 = 1,2 intersect levert dan t = 6,71 en t = 9,33 en t = 18,80 en t = 21,41 hoger dan 1,2 m is tussen 6,71 en 9,33 en ook tussen 18,80 en 21,41 samen is dat 5,23 uur. |
||||||||
| 4. | a. | Op t = 0 is de
sinusgrafiek in zijn evenwichtspunt en begint toe te nemen. Dat geldt ook voor de hoogte van punt P. |
|||||||
| b. | Dan gaat P naar beneden bewegen, en zou gelden h(t) = 18 - 14sin(1/4πt) | ||||||||
| c. | Het is dezelfde
formule als die van P alleen het beginpunt (waar de sinus door de
evenwichtslijn omhoog gaat) is anders. S begint in het onderste punt. Je zou er een gespiegelde cosinus van kunnen maken: dat geeft h(t) = 18 - 14cos(1/4πt) |
||||||||
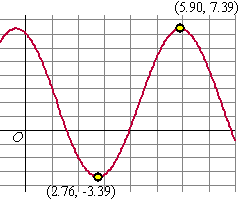
| 5. | Plot de grafiek van
Y1 = 3 - 2·sinx + 5·cosx - 1 Zie de figuur hiernaast. calc - maximum en calc-minimum geeft de punten (2.76, -3.39) en (5.90, 7.39) de evenwichtslijn is dan (-3,39 + 7,39)/2 = 2 de amplitude is 7,39 - 2 = 5,39 de halve periode is 5,90 - 2,76 = 3,14 dus de hele periode is 6,28 (zal wel 2π zijn want dat is ook de periode van y1 en y2) beginpunt is dan (2,76 + 5,90)/2 = 4,33 Formule: y = 2 + 5,39 sin(x - 4,33) |
 |
|||||||
| 6. | a. | Lees twee toppen af:
(1, 70) en (2, 30) Evenwichtslijn is dan (70 + 30)/2 = 50 Amplitude is 70 - 50 = 20 Halve periode is 2 - 1 = 1 dus de periode is 2 en in de formule staat 2π/2 = π Beginpunt is een kwart periode vσσr t = 1, dus dat is t = 0,5 Samen geeft dat h(t) = 50 + 20 sin(π(t - 0,5)) |
|||||||
| b. | Y1 = 50 + 20 sin(p(X
- 0,5)) en Y2 = 60 Intersect geeft t = 0,67 en t = 1,33 Daartussen ligt 1,33 - 0,67 = 0,67 seconden van de periode van 2 Dat is 0,67/2 100% = 33% |
||||||||
| c. | De snelheid is de
helling. Y1 = 50 + 20 sin(π(X - 0,5)) calc - dy/dx en dan X = 0,6 geeft snelheid 59,8 cm/sec. |
||||||||
| 7. | a. | 30 januari is n
= 30 B = 12,3 + 4,6 sin2π/365 (30 - 80) = 8,81 uur en dat is 8 uur en 49 minuten als de om om 8 uur 27 opkomt gaat hij om 17 uur 16 weer onder |
|||||||
| b. | Y1 = 12,3 + 4,6
sin(2*π*(X - 80)/365) en Y2 = 14 intersect geeft als eerste snijpunt X = 101,99 n = 102 is 31 + 28 + 31 + 12 dus dat is inderdaad 12 april |
||||||||
| c. | het maximum ligt bij
n = 170 en is 10,4 het minimum ligt bij n = 352 en is 7,2 Evenwichtslijn is dan (10,4 + 7,2)/2 = 8,8 Amplitude is 10,4 - 8,8 = 1,6 Halve periode is 352 - 170 = 182, dus de periode is 364: zal wel 365 dagen moeten zijn Beginpunt een kwart periode vσσr het maximum: ongeveer 79 B = 8,8 + 1,6 sin2π/365(t - 79) |
||||||||
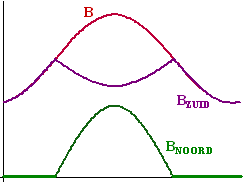
| d. | Bnoord + Bzuid
= B dus Bzuid = B - Bnoord Trek de grafiek van Bnoord van die van B af. Dat geeft de paarse grafiek hiernaast. |
 |
|||||||
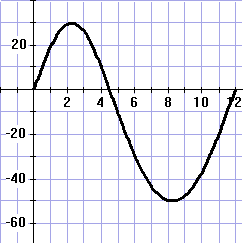
| 8. | a. | De amplitude is 30, De periode is 9, dus in de formule komt 2π/9 Daarmee wordt de formule y = 30 sin (2π/9 x) |
|||||||
| b. | Het deel tussen 4,5 en 12 is wιιr een sinusgrafiek, maar nu met amplitude 50: |
 |
|||||||
| 9. | a. | de
periode is (2π)/(0,88p)
= 2/0,88 = 2,2727 milliseconde, en dat is 0,002727
seconden de frequentie is dan 1/0,002727 = 367 trillingen per seconde. |
|||||||
| b. | De
amplitude ligt tussen 0,14 en 0,28 De periode is kleiner dan die van A en B, dus het getal in de formule voorde t is groter dan 0,88. Bijv. y = 0,2 sin(t) |
||||||||
| 10. | a. | Een
sinus is maximaal 1 en minimaal -1 De hoogte is dan maximaal 3 1 + 7 = 10m en minimaal 3 -1 + 7 = 4 m. |
|||||||
| b. | Plot de
grafiek Y1 = 3*sin(π*X/30) + 7 en
de lijn Y2 = 8 Denk erom dat je rekenmachine op radialen staat (MODE - Radian). window bijv. Xmin = 0, Xmax = 100, Ymin = 0, Ymax = 12 intersect met de juiste twee snijpunten geeft X ≈ 3,245 en X ≈ 86,755 De lengte daartussen is ongeveer 86,755 - 3,245 ≈ 84 m. |
||||||||
| c. | Het
maximum is 8 en het minimum is 4, dus de evenwichtslijn is y
= 6 en de amplitude is 2. De afstand tussen het beginpunt met hoogte 4 en het eindpunt met hoogte 6 is 3/4 periode en dat is 48 m. Een periode is dus 64 m. Kies als oorsprong bijvoorbeeld het punt waar de hoogte 6 meter is (16 meter naast het begin van de sporthalgrafiek) Dan wordt de formule: y = 6 + 2 sin(2π/64 x) |
||||||||
| 11. | 1/2p
= p - 1 + cospx cospx = 1 - 1/2p cospx heeft amplitude 1, dus als er snijpunten moeten zijn, dan moet 1 - 1/2p < 1 en 1 - 1/2p > -1 1 - 1/2p < 1 ⇒ 1/2p > 0 ⇒ p > 0 1 - 1/2p > -1 ⇒ 1/2p < 2 ⇒ p < 4 Als er bovendien minstens 4 snijpunten op het interval [0, 2π] moeten zijn, dan moet de cosinusgrafiek daar dus minstens twee periodes hebben. Dat betekent dat de periode kleiner dan π moet zijn. dus 2p/p < π ⇒ p > 2 Alles samengenomen moet gelden 2 < p < 4 Als p een geheel getal moet zijn is de enige mogelijkheid p = 3 |
||||||||
| 12. | a. | Lees af:
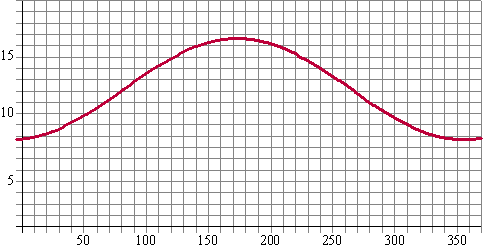
maximum (165, 21) en minimum (348, 16.5) De evenwichtslijn is dan (16,5 + 21)/2 = 18,75 De amplitude is 21 - 18,75 = 2,25 De halve periode is 348 - 165 = 183, dus de periode is 366. Laten we maar 365 van een heel jaar nemen. Een kwart periode vσσr het maximum gaat de sinusgrafiek door de evenwichtsstand omhoog, dus dat is bij ongeveer 165 - 0,25 365 = 74 Dat geeft y = 18,75 + 2,25 sin(2π/365 (x - 74)) |
|||||||
| b. | 4:19 is 4,32
uur en 8:48 is 8,80 uur 17 juni is dagnummer 181 en 30 december is dagnummer 364 Het minimum is dus (181, 4.32) en het maximum is (364, 8.80) De evenwichtslijn is dan (8,80 + 4,32)/2 = 6,56 De amplitude is 8,80 - 6,56 = 2,24 De halve periode is 364 - 181 = 183, dus de periode is 366. Laten we maar weer 365 van een heel jaar nemen. Een kwart periode vσσr het maximum gaat de sinusgrafiek door de evenwichtsstand omhoog, dus dat is bij ongeveer 364 - 0,25 365 = 273 Dat geeft y = 6,56 + 2,24 sin(2π/365 (x - 273)) |
||||||||
| c. | Daglengte: D = 18,75 + 2,25 sin(2π/365 (x - 74)) - (6,56 + 2,24 sin(2π/365 (x - 273))) |
||||||||
|
|
|||||||||
| Lees af (of gebruik
je GR met calc-maximum/minimum): minimum (356, 7.74) en maximum
(173, 16.63) De evenwichtslijn is dan (7,74 + 16,63)/2 = 12,19 De amplitude is 16,63 - 12,19 = 4,44 De periode is uiteraard weer 365 dagen Een kwart periode vσσr het maximum gaat de sinusgrafiek door de evenwichtsstand omhoog, dus dat is bij ongeveer 173 - 0,25 365 = 82 Dat geeft y = 12,19 + 4,44 sin(2π/365 (x - 82)) |
|||||||||
| 13. | a. | De rode grafiek
begint bovenaan en gaat omlaag, dus dat is het hoogste punt van de
ventilator. De blauwe grafiek begint onder de evenwichtslijn en gaat omlaag dus dat is het laagste van de twee linkerpunten van de ventilator. |
|||||||
| b. | De periode is 0,2 seconden, dus dat is 60/0,2 = 300 omwentelingen per minuut. | ||||||||
| c. | evenwichtslijn 80 amplitude 80 periode 0,2 seconden dus in de formule 2π/0,2 = 10π begin punt: na een kwart periode is het punt op de evenwichtslijn, dus een verschuiving van 0,25 0,2 = 0,05 sec. naar rechts. Dat geeft y(t) = 80 + 80sin(10π(t - 0,05)) |
||||||||
| 14. | a. | de
periode is 2π/0,212769
= 29,53054866... dagen Een dag is 24 69 = 1440 minuten Dat is dus 29,53.... 1440 = 42524 minuten |
|||||||
| b. | 22
februari ligt tussen t = 52 en t = 53 Dan is (invullen) P = 22 en P = 14 Dat is dus tussen nieuwe maan en eerste kwartier OF tussen laatste kwartier en nieuwe maan. Maar omdat P van t = 52 naar t = 53 afgenomen is (van 22 naar 14) is het tussen laatste kwartier en nieuwe maan. |
||||||||
| 15. | 2cos(1/2x
- 1/8π)
= 2cos(1/2(x
- 1/4π)) cosx heeft toppen (0, 1) en (π, -1) cos(1/2x) heeft toppen (0, 1) en (2π, -1) cos(1/2(x - 1/4π)) heeft toppen (1/4π, 1) en (9/4π, -1) 2cos(1/2(x - 1/4π)) heeft toppen (1/4π, 2) en (9/4π, -2) De lijn daar doorheen heeft a = Δy/Δx = (-2 - 2)/(9/4π - 1/4π) = -4/(2π) = -2/π 2 = -2/π 1/4π + b = geeft b = 5/2 dus het is de lijn y = -2/π x + 5/2 sin(x) heeft toppen (1/2π, 1) en (3/2π, -1) sin(x - 1/4π) heeft toppen (3/4π, 1) en (7/4π, -1) Liggen die op de lijn? -2/π 3/4π + 5/2 = -3/2 + 5/2 = 1 KLOPT -2/π 7/4π + 5/2 = -7/2 + 5/2 = -1 KLOPT OOK. |
||||||||
| 16. | a. | 3,5 =
7 + 7sin(2π/60
(x - 15)) Y1 = 3,5 Y2 = 7 + 7*sin(2*π*(X - 15)/60) intersect geeft x = 11,513 en x = 48,487 Daartussen ligt dus 36,97 m |
|||||||
| b. | Hoogte
is 12,5 dus evenwichtslijn h = 6,25 en amplitude
6,25 (beiden a) Lengte is 51 m dus in de formule staat 2π/51 = c beginpunt van de sinusgrafiek 60 + 0,25 51 = 72,75 Dat geeft h = 6,25 + 6,25 sin(2π/51(x - 72,75)) |
||||||||
| c. | Maak
er een cosinusgrafiek van die is gespiegeld. De formule wordt dan h = a - acos(2π/39 x) de bovenkant van de verdieping begint bij x = (39 - 24)/2 = 7,5 de cosinusgrafiek moet dus door (7.5, 4.5) gaan invullen: 4,5 = a - acos(2π/39 7,5) 4,5 = a - 0,3546a 4,5 = 0,6454a a = 6,972 De hoogte wordt dan 2 6,972 = 13,9 m. |
||||||||
| 17. | a. | 2 + 3sin(π(x
+ 1/4))
= 7/2 3sin(π(x + 1/4)) = 3/2 sin(π(x + 1/4)) = 1/2 π(x + 1/4) = 1/6π + k2π ∨ π(x + 1/4) = 5/6π + k2π x + 1/4 = 1/6 + 2k ∨ x + 1/4 = 5/6 + 2k x = -1/12 + 2k ∨ x = 7/12 + 2k Tussen 0 en 2 geeft dat de oplossingen x = 23/12 en x = 7/12 |
|||||||
| b. | De amplitude is 2 3 = 6 dus
q = 6 De periode is 4 dus r = 2π/4 dus r = 1/2π De grafiek van f is een sinusgrafiek met evenwichtslijn 3 en amplitude 2 en periode 2 die 1/4 naar links is geschoven, dus heeft beginpunt x = -1/4 De top daarvan bevindt zich een kwart periode naast het beginpunt, dus bij x = -1/4 + 1/2 = 1/4 Het hoogste punt van de grafiek van f is (1/4, 5) g is een cosinusgrafiek, dus die begint bij x = 1/4 dus s = 1/4 de amplitude is 6, dus de evenwichtlijn is de lijn y = -1 dus p = -1 |
||||||||
| 18. | de
snelheid varieert tussen 2,1 en 0,3 dus de evenwichtsstand is (2,1
+ 0,3)/2 = 1,2 =
a de amplitude is de afstand van evenwichtslijn tot maximum dus 2,1 - 1,2 = 0,9 = b de periode is 1 jaar, dus c = 2π/1 = 2π het maximum zit bij 3 maanden en dat is 0,25 jaar, de grafiek gaat een kwart periode daarvσσr door de evenwichtsstand omhoog, dus dat is bij t = 0, dus d = 0. |
||||||||
| 19. | a. |
-1
+ sin(2x
-
1/6π)
= -0,5 sin(2x - 1/6π) = 0,5 2x - 1/6π = 1/6π + k2π ∨ 2x - 1/6π = 5/6π + k2π 2x = 1/3π + k2π ∨ 2x = π + k2π x = 1/6π + kπ ∨ x = 1/2π + kπ Dat geeft de oplossingen x = 1/6π, 7/6π, 1/2π, 3/2π |
|||||||
| b. | De
periode van f is
2π/2
= π
dus de periode van g is 1/3π
dus b = 2π/(π/3)
= 6 = b De amplitude van f is 1, dus de amplitude van g is 0,25 Omdat de grafiek van g in het laagste punt begint, is de cosinusgrafiek gespiegeld, dus a = -0,25 f snijdt de y-as bij y = -1 + sin(2 0 - 1/6π) = -1,5 De evenwichtslijn van g is dan -1,5 + amplitude = -1,5 + 0,25 = -1,25 dus d = -1,25 |
||||||||
| 20. | De
amplitude van de onderste is 50, dus van de bovenste ook. De top van de onderste is bij 100 + 50 = 150 en dat is dus de evenwichtslijn van de bovenste. De sinussen hebben dezelfde periode, dus ook de bovenste heeft factor π/3 De voorlopige formule van de bovenste is dus Sbovenste = 150 + 50sin(π/3(x - d)) waarbij d de horizontale verschuiving is. Voor x = 0,5 is Sonderste gelijk aan 100 + 50sin(1/6π) = 125 De grafiek van Sbovenste moet dus ook door (0.5, 125) gaan. 125 = 150 + 50sin(π/3(0.5 - d)) -25 = 50sin(π/3(0.5 - d)) -0,5 = sin(π/3(0.5 - d)) -π/6 = π/3(0.5 - d)) (meer oplossingen hoeft niet: we hoeven maar ιιn d te vinden) -0,5 = 0,5 - d d = 1 dus Sbovenste = 150 + 50sin(π/3(x - 1)) |
||||||||
| 21. | |||||||||
| 22. | De
toppen zitten tussen y = 1,5 en y = -1 De evenwichtslijn is dus (1,5 + -1)/2 = 0,25 dus d = 0,25 De amplitude is 2,5/2 = 11/4 dus a = 11/4 Punt K: 3sin(1/4πx) = 11/2 sin(1/4πx) = 0,5 1/4πx = 1/6π + k 2π ∨ 1/4πx = 5/6π + k 2π x = 2/3 + k 8 ∨ x = 31/3 + k 8 Dat geeft oplossingen 2/3, 31/3, 82/3, 111/3, ... xK = 2/3 en dat is het beginpunt van de cosinus, dus c = 2/3 en xL = 111/3 dus de periode is 111/3 - 2/3 = 102/3 b = 2π/102/3 = 3/16π |
||||||||
| 23. | a. | De
eerste top van sin(x) is normaal (1/2π,
1) Door de verschuiving 3 wordt dat (1/2π, 3) Door de vermenigvuldiging factor 1/2 wordt dat (1/4π, 3) De eerste top van cos(x) is normaal (π, -1) Door de verschuiving 3 wordt dat (π, -3) Door de vermenigvuldiging factor 1/2 wordt dat (1/2π, -3) De afstand is dan √((1/4π)2 + 62) = 6,05 |
|||||||
| b. | Voer
de formule Y1 = 1 + 3sin(2x) + 1 + 3cos(2x) in
je GR in. Bereken de coφrdinaten van het eerste maximum en het eerste minimum. Dat zijn (0.3927, 6.2426) en (1.9635, -2.2426) de evenwichtslijn is (6.2426 + -2.2426)/2 = 2 de amplitude is 6.2426 - 2 = 4,24 de periode is hetzelfde als van de oorspronkelijke functies, dus in de formule staat nu 2x het beginpunt van cosinus is de top dus x = 0,39 Dat geeft h(x) = 2 + 4,24 cos(2(x - 0,39)) |
||||||||
| 24. | a. | We tellen ongeveer 5 hartslagen in 4 seconden Dat is in een minuut (60 seconden) 5 15 = 75 hartslagen. De hartslag is dus 75 slagen per minuut. |
|||||||
| b. | De evenwichtslijn is (124 + 82)/2 =
103 en dat is a De amplitude is dan 124 - 103 = 21 en dat is b De periode is 60/66 Dan is c = 2π/(60/66) = 2,2π Dat geeft P = 103 + 21sin(2,2πt) |
||||||||
| c. | De formule voor de rechte lijn van de
bloeddrukmeter is P = 170 - 10t Plot die grafiek en bepaal met je GR het eerste en laatste snijpunt van de lijn met de P-sinusoοde Dat geeft P = 128,5... en P = 91,4.... De onderdruk is 91 en de bovendruk is 129 |
||||||||
| 25. | a. | -11 + 38,6 sin(π/244
(x + 122)) = 0 Invoeren in de GR en dan calc - zero Dat geeft xA = -99,55 en xB = 99.55 De afstand daartussen is dan 199 m |
|||||||
| b. | y
= -11 + 38,6 sin(π/244
(x + 122)) herschalen met factor 1,17: y = 1,17 (-11 + 38,6 sin(π/244 (x + 122))) 1,87 omhoog schuiven: y = 1,17 (-11 + 38,6 sin(π/244 (x + 122))) + 1,87 x = 0 geeft met deze laatste formule y = 34,162 x = 0 geeft met de oorspronkelijke formule y = 27,6 De afstand is dan 6,6 m. |
||||||||
| c. | De
boog begint op 11 m onder het wegdek, en een sinusgrafiek begint op de
evenwichtsstand. Dus de evenwichtsstand is a = -11 Het hoogste punt raakt het wegdek dus de amplitude is b = 11 De breedte is 95 m en dat is de halve periode, dus de periode is 190 m, dus c = 2π/190 = 0,033 De boog begint bij x = 244/2 + 7 = 129 m, dus d = 129 y = -11 + 11 sin(0,033(x - 129)) |
||||||||
| 26. |
f(x)
= 3sin(1/2x
-
1/12π)
= 3sin(1/2(x
-
1/6π)) Het beginpunt van f is dus (1/6π, 0) De periode van f is 4π Het eerste maximum is dan (11/6π, 3) en dat is ook het maximum van g Het nulpunt van f dat samenvalt met het minimum van g is (41/6π, 0) g heeft periode 3π g heeft evenwichtslijn y = 1,5 en amplitude 1,5 g heeft beginpunt bijvoorbeeld 41/6π + 3/4π = 59/12π Dat geeft g(x) = 1,5 + 1,5sin(2/3(x - 59/12π)) |
||||||||
| 27. | a. | aflezen: het maximum is 2700 en het minimum is 2200 Dan is de evenwichtlijn gelijk aan y = 2450 dus p = 2450 Dan is de amplitude 2700 - 2450 = 250 dus q = 250 aflezen: de toppen liggen bij x = 0 en x = 5 Dan is een periode gelijk aan 5 Dan is r = 2p/5 dus r ≈ 1,26 |
|||||||
| b. | per
keer ademt hij 2 · 1200 = 2400 mL lucht in de periode is 2p/4,19 = 1,5 seconden in 1 minuut ademt hij dan 60/1,5 = 40 keer in en uit dat is 40 · 2400 mL = 96000 mL lucht Dat is 96 liter. |
||||||||
| 28. | a. | minimum 29,4 en maximum 30,5 dan is de evenwichtslijn het gemiddelde daarvan: a = 29,95 de amplitude is 30,5 - 29,95 = 0,55 dus b = 0,55 de periode is een jaar, dus c = 2p/265 dus c = 0,01721 het minimum ligt op 21 december, en dat is t = -11 het beginpunt ligt 1/4 periode rechts van het minimum, dus bij t = -11 + 91,25 = 80,25 dus d = 80 |
|||||||
| b. | Het
gewicht heeft minimum 83,87-0,24 = 83,63 en maximum 83,87 +
0,24 = 84,11 Neem 83,87 gelijk aan 100% 84,11 · 100/83,63 = 100,574% dus dat scheelt 0,574% De calorie-inname heeft minimum 2005-45 = 1960 en maximum 2005 + 45 = 2050 Neem 1960 gelijk aan 100% 2020 · 100/1960 = 104,59% dus dat scheelt 4,59% 0,574 is inderdaad kleiner dan 4,59 |
||||||||
| c. | Voer
de formules in in de GR en gebruik calc - maximum C is maximaal voor t = 319 G is maximaal voor t = 27 Van maximale C naar het eind van het jaar is 365 - 319 = 46 dagen Dan naar maximale G is nog eens 27 dagen, in totaal dus 73 dagen verschil. |
||||||||
| 29. | a. | h(t) = 75 + 60 sin(0,209(t
- d)) het laagste punt is 75 - 60 = 15 op t = 0 moet er dus 15 uitkomen: 75 + 60 sin(0,209(0 - d)) = 15 60sin(-0,209d) = -60 sin(-0,209d) = -1 -0,209d = -1,57 d = 7,5 |
|||||||
| b. | h(t) = 75 + 60sin(0,209t) h '(t) = 60cos(0,209t) · 0,209 Dat is maximaal als de cosinus gelijk is aan 1 Dan is h ' = 60 · 1 · 0,209 = 12,54 meter per minuut
?? = 3600 ·
12,54/60 = 752,4 meter per uur |
||||||||
| c. | 40000 = √(h2 + 12742000h) Y1 = 40000 Y2 = √(X^2 + 12742000X) intersect geeft h = Y = 125,56... Y1 = 125,56 Y2 = 75 + 60sin(0,209X) Intersect geeft t = 4,79 en t = 10,23 daartussen ligt 10,23 - 4,79 = 5,4 minuten Dat is afgerond 5 minuten. |
||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||