natuurlijke logaritme


De natuurlijke logaritme.	© h.hofstede (h.hofstede@hogeland.nl)

afgeleide van g^xhet getal e

Eerder ontdekten we al dat de afgeleide van g^x gelijk is aan een constante maal g^x waarbij die constante van g afhangt. We hebben de constante toen ln(g) genoemd.

f (x) = g^x ⇒ f '(x) = g^x • ln g

Deze les gaan we verder op zoek naar de eigenschappen van deze ln(g). Hoe hangt hij nou precies van g af?
Eén ding weten we al wel: Als g gelijk is aan e, dan is deze constante gelijk aan 1, ofwel ln e = 1.
Door voor een aantal waarden van g de waarde van ln(g) te benaderen kunnen we alvast een idee krijgen van de grafiek van ln(g). Dat geeft deze tabel en de grafiek ernaast.

g	0,3	0,5	2	e	3	4
ln(g)	-1,20	-0,69	0,69	1	1,10	1,39

We kunnen ontdekken wat deze ln(g) voorstelt door de afgeleide van e^ax op twee manieren op te schrijven:• De afgeleide van e^ax is met de kettingregel gelijk aan a • e^ax

• De afgeleide van e^ax = (e^a)^x dus de afgeleide is (e^a)^x • ln(e^a)
(dat was immers de regel voor de afgeleide van g^x)

Maar die twee moeten natuurlijk wel gelijk zijn!

Dus moet gelden: ln(e^a) = a en ook graag voor élke a !!!!!!
Die lnx functie zorgt ervoor dat e^x teniet wordt gedaan.
Maar dat betekent dat lnx de functie is die e^x opheft......
De inverse ervan.......
Dus moet wel gelden lnx = ^elogx

ln(x) = ^elog(x)

Deze ln(x) is dus de logaritme met grondtal e. Hij heet ook wel de natuurlijke logaritme.

Onze mysterieuze constante factor blijkt dus gewoon een logaritme te zijn; en wel de logaritme met grondtal e.
Dat betekent dat alle rekenregels voor logaritmen en eigenschappen van grafieken van logaritmen ook voor lnx gelden.
Hier zijn ze nog een keer in hun "ln-vorm";


lna + lnb = ln(ab) lna - lnb = ln(^a/_b) p • lna = ln(a^p)

OPGAVEN

Los algebraïsch op en rond je antwoord niet af:

ln(4x) = 2

x = ¹/₄e²

2 + lne² = lnx

x = e⁴

ln(x + 6) = 2lnx

x = 3

lnx + ln2x = ln(x + 1)

x = 1

ln(√x) = lnx + 2

x = e^-4

e^x^{- 1} = 4

x =1 + ln4

3lnx = lnx + 2

x = e

ln(¹/_x) = 3 + lnx

x = e^-1,5

2 • e^x = 6

x = ln3

ln(e^{2x + 1}) = x - 5

x = -6

e^ln^x = 3x - 8

x = 4

e²^x + 2 = 3e^x

x = 0 of ln2

Tussen de grafieken van y = lnx en y = ln(2x) wordt een rechthoekige driehoek getekend zoals in de figuur hiernaast. A en B zijn de snijpunten van de lijn y = p met de grafieken. C ligt op de grafiek van y = ln(2x) en hoek ABC is recht.

Bereken voor welke p de oppervlakte van driehoek ABC gelijk is aan 4ln2.

p = ln16

Gegeven zijn de functies: f(x) = e^2x en g(x) = 1 - e^-xBeiden hebben domein [-2,3]

Bereken exact een vergelijking van de raaklijn aan de grafiek van f in het punt waarvoor x = -1. Rond de getallen in je antwoord niet af!

y = 2e^-2 x + 3e^-2

Bepaal in 2 decimalen nauwkeurig de lengte van de grafiek van g(x)

10,01

De horizontale lijn y = p snijdt de grafiek van f in punt A en die van g in punt B.
Voor de lengte L van lijnstuk AB blijkt te gelden: L = -ln(√p - p√p)

Toon aan dat deze formule juist is.

is vreemd genoeg altijd een constante! Toon dat aan.

Examenopgave HAVO Wiskunde B, 2002

Wijken in een stad die dicht bij het centrum liggen zijn dichter bevolkt dan wijken verder van het centrum af.
In 1950 begon men een onderzoek naar het verband tussen de bevolkingsdichtheid in een stad en de afstand tot het stadscentrum.
De bevolkingsdichtheid D in een punt P is het aantal inwoners in een cirkelvormig gebied rond P met een oppervlakte van 1 km².
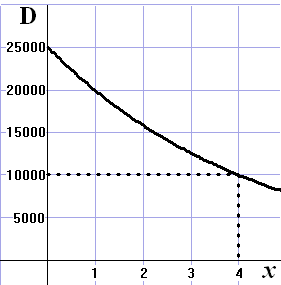
In de figuur hiernaast zie je een grafiek die voor een bepaalde stad het verband tussen de afstand x tot het stadscentrum (in km) en de bevolkingsdichtheid D weergeeft.
Uit deze grafiek kun je aflezen dat op een afstand van 4 kilometer van het stadscentrum de bevolkingsdichtheid gelijk is aan 10000 inwoners per km².

Bij de grafiek hiernaast hoort de exponentiële formule
D = a · e ^-bx. Hierin zijn a en b constanten

Bereken met behulp van de grafiek hierboven de waarden van a en b. Rond in je antwoord gevonden waarden die niet geheel zijn af op twee decimalen.

Voor een tweede stad heeft men het volgende lineaire verband tussen ln(D) en x gevonden:
ln(D) = 10 - 0,2x.

Toon algebraïsch aan dat bij benadering geldt: D = 22000 · e ^-0,2x

Examenopgave VWO Wiskunde B, 2010

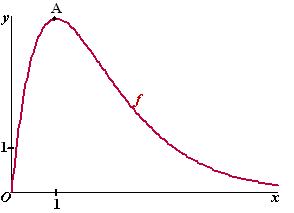
In de onderstaande figuur is voor x ≥ 0 de grafiek getekend van de functie f die gegeven is door: f (x) = ^8x/_ex

Deze grafiek heeft één top, die we A noemen.

Bereken exact de x-coördinaat van A.

x = 1

We bekijken nu voor positieve waarden van n met n ≠1 de functie g_n die is gegeven door g_n(x) = ^8nx/_ex

De grafieken van g_n snijden de grafiek van f in het punt (0, 0). Ook is er voor elke positieve waarde van n met n ≠ 1 nog een ander snijpunt.

In de volgende tabel staat voor enkele waarden van n de x-coördinaat van dit andere snijpunt.

n	2	3	4	5
x_snijpunt	ln2	¹/₂ln3	¹/₃ln4	¹/₄ln5

Voor de vier waarden van n uit de tabel geldt: x_snijpunt = ¹/_(n-1) • ln n
Hieruit ontstaat het vermoeden dat deze formule voor snijpunt x klopt voor elke positieve waarde van n met n ≠1.

Toon aan dat dit vermoeden juist is.

De longinhoud (I in liters) van mensen tot 25 jaar blijkt af te hangen van hun geslacht (man/vrouw) en hun leeftijd (J in jaren) en hun lengte (L in meters). Voor meisjes onder de 25 geldt bij benadering de formule:

I = 0,245 • e^{1,488 • L + 0,0119 •
L • J}

Bereken algebraïsch de lengte van een meisje van precies 15 jaar met een longinhoud van 2,5 liter.

1,31 m

Examenvraagstuk HAVO Wiskunde B, 2000.

Gegeven is de functie f(x) = x · e^5xDe lijn met vergelijking y = 3x snijdt de grafiek van f behalve in (0,0) ook nog in een punt A.

Bereken zonder je rekenmachine te gebruiken de x-coördinaat van A.

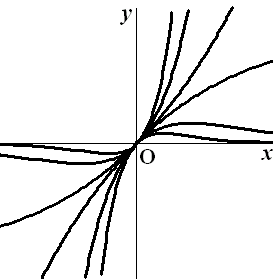
Voor elke waarde van a is gegeven de functie f_a(x) = x · e^axVoor een aantal waarden van a is in een rechthoekig assenstelsel Oxy de bijbehorende grafiek getekend. Zie de figuur hieronder.

De grafieken in de figuur hierboven lijken in (0,0) allemaal dezelfde helling te hebben.

Toon aan dat voor elke waarde van a de grafiek van f_a in (0,0) dezelfde helling heeft.

Examenvraagstuk VWO Wiskunde B, 2006

Om 15.00 uur wordt het verwarmingselement van een sauna aangezet. Vanaf dat moment wordt de sauna opgewarmd. Dan geldt: S(t) = 200 - 180 • e^-0,29t
Hierin is S de temperatuur in de sauna in graden Celsius en t de tijd in uren vanaf 15.00 uur.

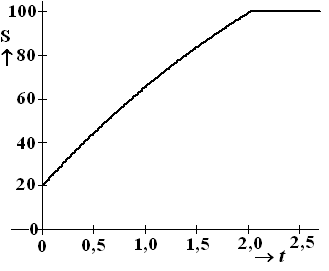
De thermostaat van de sauna is ingesteld op 100ºC. Zodra die temperatuur bereikt is, wordt het opwarmen gestopt. Vanaf dat moment wordt de temperatuur constant gehouden. In onderstaande figuur staat de grafiek van S.

Bereken hoe laat het opwarmen wordt gestopt. Geef het tijdstip in minuten nauwkeurig.

17:02

Bereken met behulp van differentiëren de snelheid waarmee de temperatuur in de sauna toeneemt om 16.00 uur. Geef je antwoord in tienden van graden Celsius per minuut.

0,7

Om bij een ingestelde temperatuur van de thermostaat uit te rekenen hoe lang de sauna nodig heeft om deze temperatuur te bereiken, kun je een formule gebruikten die t uitdrukt in S.

Druk t uit in S.