| |
 |
| Ontbinden
(1) |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
| Ontbinden in factoren
betekent: "Schrijven als vermenigvuldiging" en dat gaan
we doen door haakjes IN een vergelijking te zetten.
"WAAAAT?" hoor ik je al denken; "Wat is dit voor
flauwekul? Eerst moesten we met veel pijn en moeite leren om haakjes weg
te werken, en nou zeker weer haakjes terugzetten??? Waar is dat nou weer
goed voor? Werkverschaffing?
Het zit hem allemaal in de volgende eenvoudige vergelijking: |
|
|
|
|
|
|
In plaats van die A of die B mag
er van alles staan. Hier staat dus eigenlijk `twee dingen met elkaar
vermenigvuldigd geven als resultaat NUL.
De oplossing is eenvoudig: als twee getallen met elkaar vermenigvuldigd
NUL opleveren, dan moet minstens één van beide 0 zijn. Dus in dit
geval is de oplossing A = 0 of B = 0.
(met "of" bedoelen we in dit geval dus óf de één,
óf de ander, óf allebei. Conclusie: |
|
|
|
A • B = 0 ⇒
A = 0 of B = 0 |
|
|
|
|
|
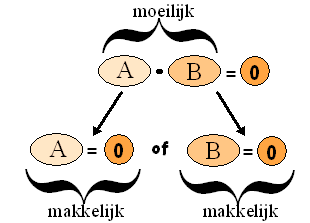
| Hiernaast zie je hoe één
moeilijke vergelijking op deze manier gesplitst kan worden in twee
(misschien) makkelijkere vergelijkingen.
Voorbeeld:
x • (x3 - 8) = 0 kun je splitsen
in
x = 0 of
x3 - 8 = 0
en x3 - 8 = 0 geeft x3
= 8 dus x = 2
Als je de haakjes in de oorspronkelijke opgave zou wegwerken krijg
je x4 - 8x = 0 en die is veel en
veel moeilijker op te lossen. |
|
|
|
| Conclusie: Soms kun je
vergelijkingen mét haakjes wel oplossen, en dezelfde zónder haakjes
niet! Elke keer als er mét haakjes alleen maar blokjes met elkaar
vermenigvuldigd staan kunnen we ons probleem splitsen in eenvoudigere
problemen. Denk erom dat dit alleen werkt als er "= 0"
staat!! Overtuigd van het feit dat haakjes best handig kunnen zijn?
Mooi.
Laten we daarom de zaak omdraaien:
Stel dat de vergelijking is x3
- 8x = 0, hadden we er dan misschien haakjes ín
kunnen zetten????? |
|
|
Het antwoord zal je
niet verbazen: Ja, natuurlijk kan dat!
Dat kun je het beste zien door je te realiseren wat er gebeurde bij het
wegwerken van de haakjes. Bij bovenstaand voorbeeld zou dat er zó
hebben uitgezien: |
|
|
|

|
|
|
De grote vraag is dus:
"Is dit proces om te keren?" ofwel: "Kunnen we
blauwe pijlen ook in omgekeerde richting volgen?"
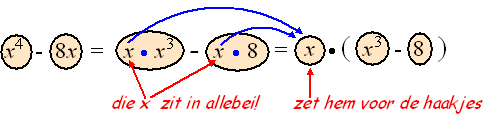
En dat is vrij makkelijk: de x vóór de haakjes heeft zich
verdeeld over alle blokjes erbinnen. Daarom staat er in elk blokje aan
de rechterkant (minstens) een x. Maar dan kunnen we vanaf al die x-en
ook de pijlen wel weer terug nemen en er weer haakjes inzetten: |
|
|
|
|
|
|
| Wat je dus moet doen als je een
vergelijking zoals die aan de linkerkant ziet, is je afvragen: "Kan
ik ook 'dubbelen' vinden:
dingen die in álle blokjes staan?"
|
| Als dat lukt (zoals met de x hierboven) dan kun je die dubbelen
uit alle blokjes halen en vóór de haakjes zetten.
Wat er overblijft staat dan nog binnen de haakjes.
Dat dubbelen zoeken kan met letters, maar ook met getallen.
Hier zijn een paar voorbeelden.
|
 |
| |
|
voorbeeld 1.
2x4 + 5x7
x4 is dubbel, kijk maar:
2x4
+ 5x4 • x3
haal x4 buiten de haakjes:
x4 • (2 + 5x3) |
voorbeeld 2. 2x2 - 4x3 heeft als
dubbele 2x2, kijk maar:
2x2 •
1 - 2x2 • 2x
haal 2x2 buiten de haakjes:
2x2 • (1 - 2x) |
voorbeeld 3.
12x3 - 8x6 + 24x4
4x3 is dubbel, kijk maar:
4x3 • 3 - 4x3 •
2x3 + 4x3 • 6x
haal 4x3 buiten de haakjes:
4x3 • (3 - 2x3 + 6x)
|
|
|
|
|
| |
|
|
|
|
|
|
|
 |
|
|
 |
|
hogere machten |
|
|
meer haakjes |
|
| |
|
|
|
|
|
|
|
|
OPGAVEN |
|
|
|
|
|
|
|
|
| 1. |
Ontbind in factoren: |
|
|
|
|
|
|
|
|
|
a. |
x6 - 2x4 |
|
f. |
4x7 + 8x5 + 12x8 |
|
|
b. |
3x5 + 6x4 |
|
g. |
9x5 + 9x4 -
18x7 |
|
|
c. |
25x5 - 5x2 |
|
h. |
12x - 3x4 |
|
|
d. |
8x6 - 12x4 + 4x5 |
|
i |
26x5 - 39x8 |
|
|
e. |
x5 + 3x6
- 2x2 |
|
j. |
2x10 - 4x3
-
14x4 |
|
|
|
|
|
|
|
|
|
| 2. |
Ontbind in factoren: |
|
|
|
|
|
|
|
|
|
a. |
21xy2 + 12x3y |
|
d. |
16p4q2
- 8qp2 |
|
|
b. |
14a3b5
- 2a3b4 |
|
e. |
2a2b2c2
- 8ab2c3 |
|
|
c. |
4pq6 - 6p2q2
|
|
f. |
12x2y2 + 6x3y4
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 3. |
Los algebraïsch op: |
| |
|
|
|
|
|
|
|
| |
a. |
x2 + 4x = 0 |
|
c. |
p5 - 4p3 = 0
|
|
| |
b. |
2x3 - 4x2
= 0 |
|
d. |
y2 = 6y |
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|
|