| |
 |
| De
balansmethode |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
Het wordt de hoogste tijd al dat
"eenvoudiger schrijven" ook eens in praktijk te gaan
toepassen.
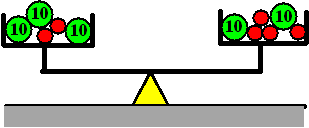
We beginnen met een verhaaltje over een weegschaal. Neem een weegschaal
met twee soorten ballen erop: groene, die 10 gram wegen en rode waarvan
we niet weten hoe zwaar ze zijn. De weegschaal is in evenwicht, kijk
maar. |
|
|
|
 |
|
|
De vraag is: Hoeveel
weegt zo'n rode bal?
Stel dat zo'n rode bal x gram weegt. Dan staat in het plaatje
eigenlijk: |
|
|
3 groene ballen plus 2 rode gelijk zijn aan 2 groenen
plus 4 roden
3 • 10 plus 2 roden = 2 • 10 plus 4 roden
30 + 2 • x = 20 + 4 • x |
|
|
Dat laatste noemen we een vergelijking.
Een vergelijking is eigenlijk elke wiskunderegel waar "=" in
staat. We zijn op zoek naar de oplossing van deze
vergelijking, ofwel wat x moet zijn zodat het klopt wat er staat.
De vergelijking die we hier moeten oplossen is dus: |
|
|
|
|
|
|
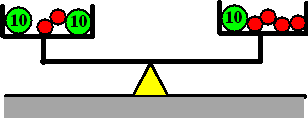
| Laten we de zaak vereenvoudigen
door van elke schaal een groene bal weg te pakken. We weten dat de
schaal daardoor in evenwicht blijft. De schaal wordt dan als hieronder.
De bijbehorende vergelijking staat er naast. |
|
|
|
 |
|
|
|
Dat ziet er al ietsje simpeler
uit.
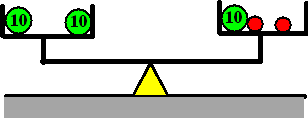
Maar wacht eens even...wat met groene ballen kan, kan natuurlijk ook met
rode ballen. Laten we van beide kanten van de weegschaal in één keer 2
rode ballen weghalen! Zolang dat maar van beide kanten gebeurt, blijft hij in evenwicht. Dat geeft het
volgende plaatje: |
|
|
|
 |
|
|
|
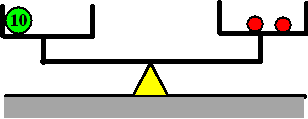
| Nou kun je niet zo veel meer aan
beide kanten weghalen. Het enige dat nog zou kunnen is één groene bal
verwijderen,. dus laten we dat maar doen: |
|
|
|
 |
|
|
|
Ik denk dat je nu wel ziet wat de
oplossing van onze vergelijking is; x moet gelijk zijn aan
5.
Als je het heel netjes en precies doet, dan moet je eigenlijk zeggen:
"We nemen nu van beide kanten van de weegschaal de helft. Dan
blijft aan de ene kant één rode bal over en aan de andere kant een
halve groene: die weegt 5 gram. Dus x = 5"
Deze methode heet heel toepasselijk de "BALANSMETHODE"
Wat is er nou stap voor stap wiskundig gezien gebeurd? |
|
|
| vergelijking |
wat is er gebeurd? |
nieuwe vergelijking |
eindresultaat |
|
|
|
|
| 30 + 2x = 20 + 4x |
beide kanten "min 10" |
30 + 2x - 10 = 20 + 4x
- 10 |
20 + 2x = 10 + 4x |
| 20 + 2x = 10 + 4x |
beide kanten "min 2x" |
20 + 2x - 2x = 10 + 4x - 2x |
20 = 10 + 2x |
| 20 = 10 + 2x |
beide kanten "min 10" |
20 - 10 = 10 + 2x
- 10 |
10 = 2x |
| 10 = 2x |
beide kanten "de helft nemen" |
5 = x |
5 = x |
|
|
|
|
|
| Het had natuurlijk ook wel wat
efficiënter gekund. In de eerste stap haalden we 10 weg en in de derde
stap nog een keer. Dat had ook wel in één keer gekund, dus direct 20.
Dan zou de balansmethode er zó uit hebben gezien: |
|
|
| vergelijking |
wat is er gebeurd? |
nieuwe vergelijking |
eindresultaat |
|
|
|
|
| 30 + 2x = 20 + 4x |
beide kanten "min 20" |
30 + 2x - 20 = 20 + 4x
- 20 |
10 + 2x = 4x |
| 10 + 2x = 4x |
beide kanten "min 2x" |
10 + 2x - 2x = 4x
- 2x |
10 = 2x |
| 10 = 2x |
beide kanten "de helft nemen" |
5 = x |
5 = x |
|
|
|
|
|
 |
|
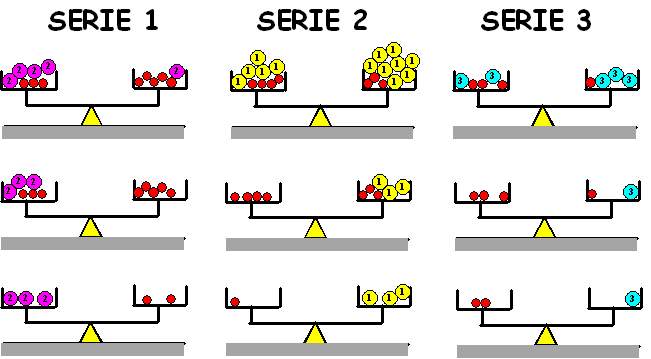
| 1. |
Hieronder staan drie series balansen
(bijbehorende onder elkaar) Leg uit welke vergelijking bij elke
balans hoort en hoe die vergelijking werd opgelost, en wat nou
de uiteindelijke oplossing is. |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
| 2. |
Los de volgende vergelijkingen met de
balansmethode op: |
|
|
|
|
|
|
|
|
|
|
a. |
6x + 2 = 4x + 10 |
|
|
d. |
10x + 1 = 5 + 8x |
|
|
b. |
5x + 3 = 4x + 8 |
|
|
e. |
1 + 2x = 6 + x |
|
|
c. |
3 + 7x = 5x + 5 |
|
|
f. |
8 + 6x = 3x + 12 |
|
|
|
|
|
|
|
|
|
|
|
| Hoe
zit dat nou precies met die laatste stap? |
|
Na het heen en weer
verplaatsen van de blokjes eindigen we altijd met aan beide kanten nog
één blokje; aan de ene kant met een letter, aan de andere kant een
getal.
Dat ziet er altijd ongeveer zó uit: |
|
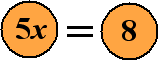 |
|
|
Er staan nog maar
twee blokjes, dus heen en weer schuiven met blokjes helpt niet meer.
Toch willen we graag het getal 5 bij de x weghalen (ons doel is
immers te krijgen x = ....).
De oplossing is vrij eenvoudig: deel beide blokjes door 5: Neem van
beide schalen één-vijfde deel!!!!!
Dan krijg je aan de linkerkant 5x/5
en dat is gelijk aan x.
Aan de rechterkant krijg je 8/5 en dat is
1,6.
Conclusie: x = 1,6
|
| Als je van "a
• x" het getal a weg wilt
halen, dan deel je beide kanten door a |
|
|
|
| Kan
het ook met negatieve getallen? |
|
|
| Jazeker! Kijk maar naar het
volgende voorbeeld. |
|
|
|
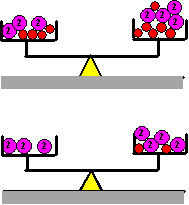 |
Zoals je ziet was de
oorspronkelijke vergelijking
6 + 4x = 8 + 6x
Eerst is op elke schaal 4x weggehaald.
Dan blijft de onderste figuur over: 6 = 2x + 8.
Maar nu willen graag die 8 daar bij de x weg hebben, dus zouden
we graag gewoon van beide schalen 8 afhalen. Helaas ligt op de andere
schaal maar 6!
De oplossing is eenvoudig: gewoon tóch 8 weghalen!
Wat krijg je als je 6 hebt en je haalt er 8 vanaf? Juist!
-2 natuurlijk. |
|
|
De vergelijking wordt dan -2
= 2x
Als je nu beide kanten deelt door 2 dan geeft dat x = -1. De balansmethode werkt nog
steeds!
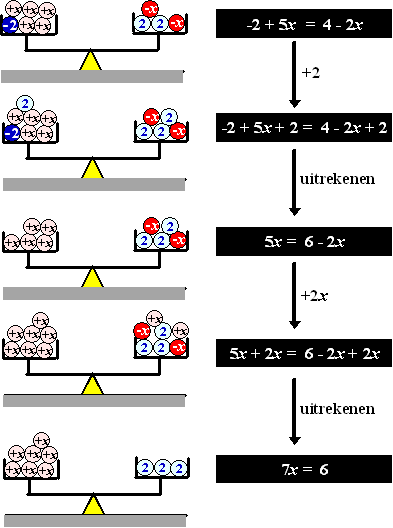
En ook als er op de schalen al negatieve getallen liggen blijft de
balansmethode geldig. Het ziet er misschien een beetje raar uit, maar
zó zou zo'n balans eruit zien met negatieve getallen, bijvoorbeeld met
de vergelijking -2 + 5x = 4 - 2x: |
|
|
|
 |
|
|
Van de eerste balans naar de
tweede zie je dat je, om een bal -2 weg te krijgen, gewoon bij beide
schalen +2 optelt. Die +2 en -2 vallen op die linkerschaal tegen elkaar
weg: worden samen nul!
Op dezelfde manier is van de derde naar de vierde schaal -2x
weggehaald door bij beide schalen +2x op te tellen.
De uiteindelijke oplossing wordt natuurlijk x = 6/7
(laatste stap: beide kanten delen door 7). |
| Dat gedoe met die schalen wordt
wel een beetje overdreven en gezocht op deze manier. Wat moet je je
voorstellen bij een negatief getal op een weegschaal? Misschien een
soort ballonnetje dat hem omhoogtrekt of zo?
Laten we ophouden met die flauwekul en het voortaan gewoon in
wiskundetaal formuleren.
Onthoud gewoon dat je vergelijkingen zó kunt vereenvoudigen: |
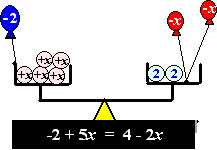 |
|
|
|
om PLUS weg te halen moet je beide kanten
MIN doen.
om MIN weg te halen moet je beide kanten PLUS doen.
om KEER weg te halen moet je beide kanten GEDEELD DOOR doen |
|
|
|
| Misschien is het (zeker in het
begin) handig om tussen de vergelijkingen te schrijven wat je doet. Dat
zou er bijvoorbeeld zó uit kunnen zien: |
|
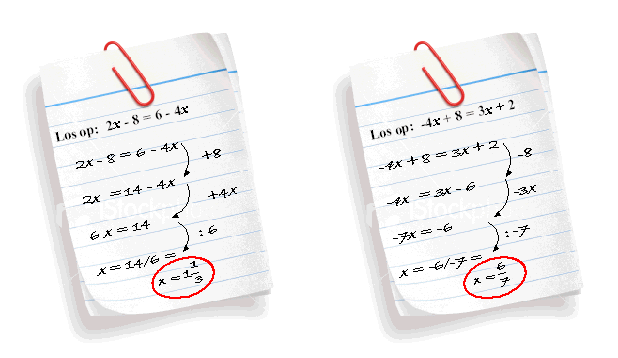 |
|
|
| 3. |
Los op: |
|
|
|
|
|
|
|
|
|
a. |
2x - 4 = 5 + 6x |
|
|
g. |
4x + 2x + 5 = x
- 7 |
|
|
b. |
3x + 12 = 8x - 3 |
|
|
h. |
3x = 1 - 2x + 6 |
|
|
c. |
-2x + 5 = 10 + 4x |
|
|
i. |
0 = 4x + 3 - 5x |
|
|
d. |
3 + 2x + 1 = 6x + 2 |
|
|
j. |
-2x - 5 = -6
- 4x |
|
|
e. |
5 - 5x = 2 + 2x |
|
|
k. |
2x + 3x - 4 = 5 + 7x
- 2 |
|
|
f. |
2x + 3 = 1/2x
+ 12 |
|
|
l. |
x + 4 = 6x - 12 |
|
|
|
|
|
|
|
|
|
|
| |
|
| 4. |
Kyra en Gwen beginnen tegelijk, en in hetzelfde
tempo getallen op te noemen.
Kyra begint bij 2012 en neemt elk volgend getal steeds 7 lager.
Haar rij is dus 2012 - 2005 - 1998 - ....
Gwen begint bij 80 en neemt elk volgens getal steeds 3 hoger.
Haar rij getallen is dus 80 - 83 - 86 - ...
Wat is het kleinste verschil tussen de getallen die zij tegelijk
noemen dat zal voorkomen? |
| |
|
|
|
|
|
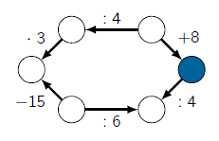
| 5. |
Vlaamse
Olympiade.
Welk getal hoort thuis in de gekleurde cirkel? |
| |
 |
| |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| Kunnen
er nog rare dingen gebeuren? |
|
|
|
|
|
|
|
|
Hûh?
|
|
Het kan gebeuren dat
tijdens de balansmethode alle x-en verdwijnen! Raar hé?
Neem bijvoorbeeld de volgende vergelijking:
Los op: 4x + 8 = x + 3 + 3x |
|
|
|
⇒
4x + 8 = 4x + 3
⇒ 8 = 3 |
|
|
|
|
|
|
Wat moet je in zo'n geval doen?
Ik zou in paniek raken.....
Er zijn twee mogelijkheden: |
|
|
|
|
|
|
| Mogelijkheid
1: Je krijgt iets wat niet klopt. |
|
Zoals in het voorbeeld
hierboven: 8 is duidelijk niet gelijk aan 3.
In dat geval is de enige conclusie: "Er is geen enkele x
waarvoor dit klopt"
Conclusie: |
| |
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Mogelijkheid
2: Je krijgt iets wat altijd klopt. |
| |
Als de opgave was geweest los
op: 4x + 8 = x + 8 + 3x dan had je
gevonden 8 = 8
Dat is duidelijk altijd waar! Kennelijk doet het er niet toe wat
je kiest voor x. Alles mag.
Conclusie: |
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
 |
|
|
 |
|
mintekens |
|
|
haakjes |
|
|
|
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|