© h.hofstede (h.hofstede@hogeland.nl)
 
Ik hoop dat je verzonnen hebt dat die 3x2 - 2x precies de afgeleide is van  x3 - x2 .
Als dat gelukt is, dan heb je de essentie van deze les door! (als het niet gelukt is heb je te vroeg geclickt!!!)

Als je dat eenmaal gezien hebt, dan vergeet je die  3x2 - 2x voorlopig even. Immers als je x3 - x2 als een blokje X ziet, dan komt met de kettingregel straks vanzelf  3x2 - 2x tevoorschijn.
Dan staat er  1/X.
De primitieve daarvan is ln│X│,  in dit geval dus:    F(x) = ln│x3 - x2│ + c

Controleer zelf maar door te differentiëren dat alles precies goed komt. Maar dat wisten we natuurlijk al.....
       
Soms moet je eerst wat werk verrichten.
Soms staat die afgeleide er niet helemaal maar wel bijna.
In die gevallen kun je proberen om die afgeleide compleet te maken.

Voorbeeld 1.
Neem de functie  f(x) = x • √(x2 + 3)
Die x is ongeveer de afgeleide van x2 + 3, maar net niet helemaal, het zou 2x moeten zijn.
Nou; dan maken we dat er van:  f(x) = 1/2 • 2x • √(x2 + 3)
Nu is 2x de afgeleide van  x2 + 3, dus we kunnen die 2x even vergeten en doen alsof er staat 1/2 • √X,  en de primitieve van √X  dat is  2/3X√X
De primitieve is dan 1/2 • 2/3 • X√X = 1/3 •(x2 + 3)√(x2 + 3)
       
Voorbeeld 2:  Een beroemde toepassing.

Neem de functie f(x) = tanx
Dat is hetzelfde als  f(x) = sinx/cosx 
Maar die sinx is ongeveer de afgeleide van cosx!  Op een minteken na.
Dus als je schrijft  f(x) = - - sinx/cosx   dan kun je die -sinx even vergeten, en als je cosx als X ziet staat er  f(X) = -1/X
De primitieve daarvan is  uiteraard  -ln│X│ + c
Dus dat wordt hier:    F(x) = -ln│cosx│ + c.  Een resultaat om trots op te zijn:
       

de primitieve van f(x) = tanx    is    F(x) = -ln│cosx│+ c
       
Voorbeeld 3:  Een gemeen voorbeeld.
       
Neem de functie  f(x) = lnx/x  .  Zie je dat onze methode hier ook werkt?
Misschien zie je het beter als je schrijft  f(x) = lnx • 1/x  ???
Precies! Die 1/x is de afgeleide van lnx.  Dus kun je de functie zien als f(X) = X
De primitieve is  F(X) = 1/2X2 + c  dus dat wordt hier  F(x) = 1/2ln2x + c
       
             
 OPGAVEN
             
1. Geef primitieven van de volgende functies:
             
  a. f(x) = (2x - 1)√(x2 - x)   h. f(x) = x • ln(2x2 + 1)  
             
  b.  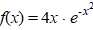 i.  
             
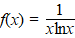  c. f(x) =  x2 •(x3 - 1)4   j. f(x) = 2cosx • sin3x  
             
  d. f(x) = sin(2x) • cos(2x)   k.  
             
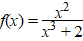  e. f(x) = sin3x   l.  
             
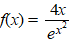  f. f(x) = (1 - 1/x ) • cos(x - lnx)   m. f(x) = x2 • (3 - 10x3)4  
             
  g.  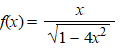 n.  
             
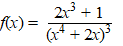2. Geef primitieven van de volgende functies:
             
  a. sin(1 - x) • (2 - cos(1 - x))4
             
  b. cos(3x) • sin10(3x)
             
  c.
             
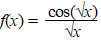  d.
             
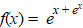  e
             
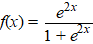3. Bereken algebraïsch de volgende integralen:
             
  a.    

15484/5
             
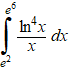  b.    

sin(1)
             
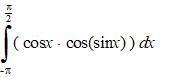  c.    

-1/2(e1 - e100)
             
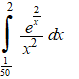4. examenvraagstuk VWO , 1983
             
  Gegeven zijn de functies met domein R+:
 

             
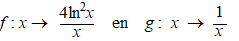  a. Los op:  f(x) ≥  g(x).
             
  b. Bereken de oppervlakte van het vlakdeel, ingesloten door de grafieken van f en g.
             
5. examenvraagstuk VWO, 1984
             
  Met domein [0, 2π] is voor elke p ∈ R gegeven de functie: fp(x) = sin2x cosx - pcosx
Bereken de oppervlakte van het vlakdeel ingesloten door de grafiek van f4 en de x-as.
             
6. examenvraagstuk VWO Wiskunde B, 1990.
             
 
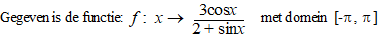  Ten opzichte van een rechthoekig assenstelsel Oxy is K de grafiek van f.
             
  a. Bereken de oppervlakte van het vlakdeel ingesloten door K en de x-as.
             
  b. Los op:  f(x) • f(-x) = 9/7.
             
7. examenvraagstuk VWO Wiskunde B, 1999.
             
 
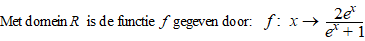  Hieronder is de grafiek van f getekend.
             
 

             
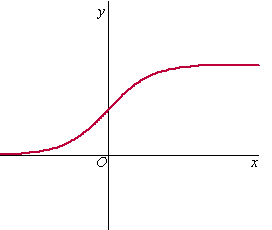  Voor a > 0 is Va het vlakdeel begrensd door de grafiek van f, de lijnen x = -a en x = a  en de x-as.

Bewijs dat de oppervlakte van Va gelijk is aan 2a.
             
8. examenvraagstuk VWO Wiskunde B, 2000.
             
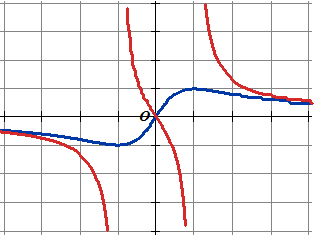
  Voor  p > 0 zijn gegeven de functies:
 

         
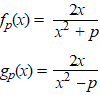  Hiernaast staan de grafieken van f1 en g1 getekend.

De raaklijn aan de grafiek van fp in O(0,0) snijdt de grafiek van gp in het punt A met positieve x-coördinaat.
De projectie van A op de x-as is het punt B.

Bewijs dat de oppervlakte van het vlakdeel dat ingesloten wordt door de grafiek van fp, de x-as en de lijn AB onafhankelijk is van p.
             
             
9. De primitieve van  √(1 + cosx) is niet zomaar makkelijk te vinden. Maar met een beetje hulp is er toch een kettingregel te ontdekken.
             
  a. Vermenigvuldig √(1 + cosx)  met   √(1 - cosx)/√(1 - cosx)
Toon daarmee aan dat  √(1 + cosx) = sinx/√(1 - cosx) 
             
  b. Geef een primitieve van √(1 + cosx)
             
10. Het vlakdeel, ingesloten door de grafiek van  g(x) = lnx/√x en de x-as en de lijn x = e  wordt gewenteld om de x-as.
Bereken de inhoud van het omwentelingslichaam dat zo ontstaat.
           

π/3
             
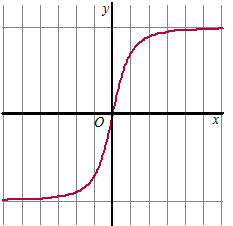
11.

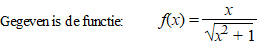  Zie de grafiek hiernaast.

V is het vlakdeel, ingesloten door de grafiek van f, de x-as en de lijn x = p.  (p > 0)
         
  Bereken p als de oppervlakte van V gelijk is aan 1
         
   

√3
             
             

© h.hofstede (h.hofstede@hogeland.nl)