Wat is kans?

© h.hofstede (h.hofstede@hogeland.nl)
Het woord kans kom je eigenlijk overal tegen:  in het dagelijks leven, in de kranten, in de reclame, noem maar op.
Een paar typische kans-uitspraken:
1.  Deze loterij geeft U de grootste kans om miljonair te worden!
2.  De kans om bij mens-erger-je-niet tweemaal achter elkaar 6 te gooien is 1 op de 36.
3.  De kans op een ongeluk bij een vliegtuigvlucht is bij onze maatschappij slechts 1 op de 1.000.000.
4.  De kans om betrapt te worden als je je belastingformulier vals invult is ongeveer 20%.
5.  De kans dat iemand van 30 jaar oud nog 90 wordt is slechts  4%.
6.  De kans op Full-House bij poker is, als je vijf kaarten krijgt, ongeveer 0,0014.
7.  De betrouwbaarheid van deze test is 95%. Dus de kans dat het klopt is 95%
8.  Zwartrijders hebben een kans van  12% om in een jaar gepakt te worden.
9.  Ik heb een letter in gedachten. De kans dat jij die letter raadt is ongeveer 0,0385.
10.De kans dat het op een dag in maart in Nederland regent is 80%.
Wat betekent dat allemaal?
Deze kansen zijn eigenlijk steeds twee getallen op elkaar gedeeld. We tellen steeds hoe vaak iets voorkomt. Als iets vaak voorkomt is de kans erop groot, als iets minder vaak voorkomt is de kans erop klein. Om de kans ergens op te krijgen delen we het aantal keer dat het voorkomt door het totaal aantal keer dat we bekeken hebben..
Dat geeft een getal tussen 0 en 1 (een percentage als je het met 100 vermenigvuldigt).
Voor de 10 voorbeelden hierboven zou dat het volgende kunnen betekenen:
   
1 Bij onze loterij is de verhouding  aantal prijzen/totaal aantal loten  het grootst.
2 Voor twee keer gooien met een dobbelsteen zijn er 36 mogelijke uitkomsten. Ik heb ze allemaal opgeschreven.
Eén van die 36 is de worp 6-6.  kans  = 1/36
3 aantal vluchten met een ongeluk/totaal aantal vluchten = 0,000001
4 We hebben een enquête gehouden en mensen gevraagd of ze hun formulier eerlijk invulden en of ze betrapt zijn.
Van de 2000 vals-invullers waren er 400 betrapt.  kans = 400/2000
5 We hebben 12000 mensen van 30 jaar oud nog 60 jaar lang in de gaten gehouden.
Na die 60 jaar leefden nog  480 mensen van hen.   kans = 480/12000
6 We hebben een computer 10000000 pokerhanden willekeurig laten schudden. Bij 14000 handen had je Full-House.
kans = 14000/10000000
7 Van elke 100 tests die we doen geven er gemiddeld 5 een foute uitslag.
Dus geven 95 een goede uitslag:  kans = 95/100
8 We hebben een groep van 1000 mensen gevraagd expres een jaar zwart te gaan rijden (dus geen wegenbelasting te betalen). We beloofden ze om de eventuele boete voor hen te zullen betalen. We moesten dat jaar 120 boetes betalen.  kans = 120/1000
9 Ik heb dit spelletje met  2000 mensen gespeeld en 77 hadden het goed.  kans  = 77/2000
10 Het KNMI heeft de afgelopen jaren van alle dagen bijgehouden of het regende of niet. Daarvan waren 1500 dagen in maart en op 1200 van die getelde dagen regende het.  kans = 1200/1500
   
Een adder onder het gras!
Kleine Graddus gooit met twee dobbelstenen en telt de aantallen ogen bij elkaar op. Hij wil de kans berekenen dat er 8 uit zal komen. Zijn redenering gaat als hiernaast.

Wat is daar fout aan?

Het zit hem erin dat niet alle 11 uitkomsten even hard meetellen. Bijvoorbeeld 5 kun je gooien op vier manieren (1,4)(4,1)(2,3)(3,2), en  7 kun je gooien op zes manieren (1,6)(6,1)(2,5)(5,2)(3,4)(4,3). De regel van gunstig/mogelijk geldt alleen bij "gelijkwaardige" uitkomsten.

Wanneer zijn uitkomsten gelijkwaardig? Je mag natuurlijk niet zeggen "als de kans erop even groot is" want dan gebruik je het begrip kans in de definitie van kans, en dat mag natuurlijk niet. Meestal wordt "gelijkwaardig" beredeneerd vanuit symmetrie-eigenschappen. Zoals hier, dat elk aantal ogen gelijkwaardig is, dus elk paar ook.

TWEE SOORTEN BEREKENINGEN:  Theoretisch en Experimenteel.
Om kansen te berekenen of te schatten hebben we hierboven gezien dat je moet uitrekenen

Maar hoe bereken of bepaal je die aantallen mogelijkheden?
Daarvoor zijn twee manieren:

De eerste is de experimentele manier (heet ook wel empirisch). Je gaat gewoon veel gegevens verzamelen (steekproeven houden, enquêtes laten invullen, metingen verrichten, noem maar op). Dan tel je gewoon het gunstige aantal gevallen dat is voorgekomen, en deelt dat door het totaal aantal gevallen. Als je maar genoeg gegevens verzamelt (hoe meer hoe beter) zal dat vrij nauwkeurig de gevraagde kans opleveren.
voorbeeld:
Je wilt graag weten hoe groot de kans is dat iemand die bij Albert Hein zijn boodschappen doet meer dan €40,- uitgeeft. Nou, ga een AH-winkel in en vraag gewoon heel vele klanten voor hoeveel geld ze hebben gekocht.
Als van de 500 gevraagde mensen er  120 meer dan €30 hebben uitgegeven, dan zal de kans dus ongeveer 120/500 = 0,24 zijn.
De tweede is de theoretische manier. Vanachter je bureau kun je de kans ergens op beredeneren. Je hoeft er geen "veldwerk" voor te verrichten, geen stap buiten de deur te zetten. Je kunt beredeneren wat het aantal gunstige mogelijkheden is en ook wat het totaal aantal mogelijkheden is. 
voorbeeld:
 Je wilt graag weten hoe groot de kans is, dat drie muntstukken die je laat vallen alle drie op "KOP" terechtkomen. Omdat een muntstuk nou eenmaal niet op zijn rand terechtkomt, en omdat KOP en MUNT gelijkwaardige mogelijkheden zijn, komen alle mogelijkheden voor drie muntstukken,  KKK, KKM, KMK, MKK, KMM, MKM, MMK, MMM,  even vaak voor. Dat zijn 8 gelijkwaardige mogelijkheden waarvan er eentje KKK is. De kans is daarom  1/8 = 0,125.
1. Welke van de 10 hierboven genoemde kansen zijn (in principe) theoretische kansen en welke zijn experimentele kansen?
       
2. Iemand kiest willekeurig één van de 64 velden van een schaakbord en zet er een witte koning op.
Daarna kiest hij willekeurig één van de overgebleven velden en zet er een zwarte toren op.

Wat is de kans dat de koning niet schaak staat? 
     

14/63
3. Drie studenten,  Albert, Berend en Chris, hebben een aantal keren een muntstuk gegooid, en telkens genoteerd of er KOP of MUNT uitkwam. Ze hebben per serie van 10 worpen het aantal keer KOP in een tabel gezet.
Dat gaf de volgende drie tabellen:
Albert
worp nr. 1 - 10 11 - 20 21 - 30 31 - 40 41 - 50
aantal 6 4 8 7 6
Berend
worp nr. 1 - 10 11 - 20 21 - 30 31 - 40 41 - 50 51 - 60 61 - 70 71 - 80 81 - 90
aantal 6 5 3 6 9 4 2 4 6
Chris
worp nr. 1 - 10 11 - 20 21 - 30 31 - 40 41 - 50
aantal kop 2 1 6 8 7
a. Na 20 worpen was één van de drie ervan overtuigd dat hij een valse munt had. Wie was dat?
Hoe was zijn conclusie na 50 worpen?
   

Chris
b. Wie heeft er na afloop de meeste reden om te concluderen dat hij een valse munt heeft?
   

Albert
c. Wie heeft er na afloop de meeste reden om te concluderen dat hij een zuivere munt heeft?
Welke twee redenen heeft hij daarvoor?

Berend
4. Om de polishoogte voor hun levensverzekeringen te kunnen berekenen maken veel verzekeringsmaatschappijen gebruik van sterftetabellen.
Hiernaast staat een tabel waarin voor 1000000 pasgeborenen is bijgehouden hoeveel er op een bepaalde leeftijd nog in leven waren (de gegevens hiernaast zijn afkomstig uit België)
leeftijd aantal nog in leven
0 1000000
5 993664
10 992839
15 992081
20 988964
25 983332
30 977567
35 971869
40 964700
45 953871
50 935934
55 909457
60 869793
65 814609
70 731998
75 613710
80 455616
85 275347
90 117039
95 29030
100 3516
a. Hoe groot is de kans dat een pasgeboren baby de leeftijd van  65 jaar haalt?

0,8146
b. Hoe groot is de kans dat een pasgeboren baby vóór zijn 40ste sterft?

0,0353
c. Hoe groot is de kans dat een Belg van 30 jaar ook nog 80 jaar wordt?

0,4661
     
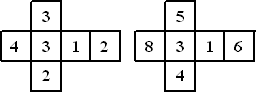
5. De Sicherman Dobbelstenen.

Hiernaast zie je de uitslagen van twee Sicherman- dobbelstenen.
Kijk wat er gebeurt als je beide stenen tegelijk gooit en het totaal aantal telt.
Maak een tabel met alle mogelijkheden en hun uitkomsten en vergelijk die met twee ""normale" dobbelstenen.

       
6. Stel dat je een aap hebt geleerd om toetsen van een keyboard met 26 toetsen, met daarop de letters van het alfabet, één voor één in te drukken.
Laat die aap een aantal toetsen indrukken.
Hoe groot is de kans dat de zin van de aap begint met IKBENEENAAP?
     

8,4  • 10-8
       
7.

Olympiadevraagstuk
Vijf klanten moeten elk een ander bedrag betalen aan een bedrijf. 
Een niet aandachtige boekhouder schrijft de vijf namen in willekeurige volgorde op de rekeningen. 
Een slaperige secretaresse steekt de vijf rekeningen in willekeurige volgorde in vijf geadresseerde enveloppen. 
Een luie koerier steekt de vijf enveloppen in willekeurige volgorde in de brievenbussen van de vijf klanten. 

Wat is de kans dat elke klant het juiste bedrag op de rekening in zijn brievenbus vindt?
     

5,8  • 10-7
       
8. Van een houten kubus kiest men willekeurig twee zijvlakken en schildert die rood.
Hoe groot is de kans dat de twee geschilderde zijvlakken aan elkaar grenzen?
     

0,8 
       
9. Twee koppels gaan samen naar het theater.
Ze gaan willekeurig op 4 naast elkaar liggende plaatsen zitten.
Hoe groot is de kans dat niemand naast zijn eigen partner zit?
     

1/3

       
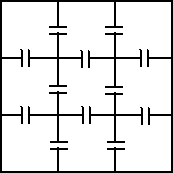
10. Een huisbaas heeft 9 kamers te huur, allemaal via deuren met elkaar verbonden (zie hiernaast).
Je huurt er willekeurig 3 van.
Hoe groot is de kans dat je door jouw drie kamers kunt lopen zonder in een andere kamer te komen?

     

22/84

   
 
   
Kansen uit Kruistabellen.

Het mooiste is natuurlijk dat iemand anders al alle gegevens voor jou heeft verzameld en dat jij uit die gegevens alleen nog maar de kansen hoeft uit te rekenen.
Neem de volgende tabel waarvoor iemand aan heel veel mensen (om precies te zijn 4800) de schoenmaat en de lengte heeft gevraagd, en dat heeft gesplitst in de mogelijkheden  lengte > 185 cm en lengte £ 185 en schoenmaat ³ 43 en schoenmaat < 43.
Dat gaf het volgende resultaat:
   
  lengte tot.
> 185 cm  ≤185 cm
schoenmaat ≥ 43 1250 993 2243
< 43 302 2305 2607
tot. 1552 3298 4850
   
Zo'n tabel waar twee grootheden tegen elkaar zijn uitgezet heet een kruistabel.
Daaruit kun je allerlei kansen berekenen.
Bijvoorbeeld:
       
  vraag: hoe groot is de kans dat iemand langer dan 185 cm is?
  antwoord: dat zijn er  1552  van de  4850  dus de kans is  1552/4850 = 0,32
           
  vraag: hoe groot is de kans dat iemand schoenmaat kleiner dan 43 heeft?
  antwoord: dat zijn er  2607  van de 4850 dus de kans is 2607/4850 ≈ 0,54
           
  vraag: hoe groot is de kans dat iemand kleiner of gelijk aan 185 cm is, en schoenmaat minder dan 43 heeft?
  antwoord: dat zijn er  2305  van de 4850 dus de kans is  2305/4850 ≈ 0,48 
           
Allemaal direct uit die tabel af te lezen.

Het wordt interessanter als je wat "ingewikkelder" vragen gaat stellen, bijvoorbeeld:
           
  vraag: hoe groot is de kans dat iemand, die langer 185 cm is, schoenmaat  groter of gelijk aan 43 heeft?
           
Het venijn van deze vraag zit hem in het stukje  "die langer 185 cm is". 
Dat betekent namelijk dat al vaststaat dat de persoon langer dan 185 cm is. Het gaat niet om de kans op langer dan 185 cm, nee, we weten vooraf al zeker dat de persoon langer is dan 185 cm. Dat betekent dat alle personen kleiner dan 185 uit de tabel niet meer meedoen voor het berekenen van deze kans. De tabel ziet er dan zo uit:
           
  lengte    
> 185 cm  
schoenmaat ≥ 43 1250    
< 43 302    
tot. 1552    
           
Groter of gelijk aan schoenmaat 43 zijn er dus nu  1250 van de 1552, dus de kans is  1250/1552 ≈ 0,81.
Omdat dit een kans is die onder een bepaalde voorwaarde (> 185 cm) geldt, noemen we dit een voorwaardelijke kans. Later zullen we daar nog uitgebreid wat lessen aan besteden.

De volgende  vraag kan natuurlijk ook:
Ik kom iemand tegen, en zie meteen dat zijn schoenen minstens maat 43 hebben. Hoe groot is de kans dat hij langer is dan 185 cm?
Nu is de voorwaarde (dat wat al vast ligt) dat zijn schoenmaat minstens 43 is, dus nu valt iedereen met schoenmaat kleiner dan 43 af. Dan blijft dit over van de tabel:
           
  lengte tot.
> 185 cm  £185 cm
schoenmaat ³ 43 1250 993 2243
         
       
           
Langer dan 185 cm dat zijn er nu 1250 van de 2243, dus de kans is  1250/2243 ≈ 0,56
           
           
11. In de volgende tabel staan van de leerlingen van drie brugklassen de leeftijden.
           
 
  klas
B1A B1B B1C totaal
leeftijd 10 jaar 2 0 4 6
11 jaar 8 7 4 19
12 jaar 12 14 9 35
13 jaar 5 8 8 21
totaal 27 29 25 81
           
  a. Hoe groot is de kans dat een willekeurige leerling ouder dan 11 jaar is?
         

56/81
  b. Hoe groot is de kans dat een leerling die niet in B1A zit, 12 jaar oud is?
         

23/54
  c. Hoe groot is de kans dat een willekeurige leerling niet in B1A zit en 12 jaar oud is?
   

23/81
  d. Hoe groot is de kans dat een leerling, die jonger dan 12 jaar is, in klas B1C zit?
         

8/15
           
12. Bij een verkeerstelling op een druk kruispunt is van een aantal auto's bijgehouden uit welke richting ze het kruispunt naderden en in welke richting ze het kuispunt verlieten. Dat geef de volgende tabel.
           
 
  VAN richting:
Noord Oost Zuid West totaal
NAAR
richting:		 Noord 0 54 32 92 178
Oost 43 0 15 45 103
Zuid 89 12 0 4 105
West 102 88 23 0 213
totaal 234 154 70 141 599
           
  a. Hoe groot is de kans dat een willekeurige auto van Noord naar West gaat?
         

102/599
  b. Hoe groot is de kans dat een auto die in richting Zuid vertrekt, uit richting Oost kwam?
         

12/105
  c. Hoe groot is de kans dat een willekeurige auto op de kruising rechtdoor rijdt?
         

254/599
  d. Hoe groot is de kans dat een willekeurige auto die vanuit het Noorden aankomt  niet naar het Oosten vertrekt?
         

191/234
           
13. Vier mensen gaan samen uit eten. Ze gaan elk een maaltijd bestellen, bestaande uit een voorgerecht, een hoofdgerecht en een nagerecht. Het restaurant heeft de beschikking over  6 verschillende voorgerechten, 9 hoofdgerechten en 5 nagerechten.

Hoe groot is de kans dat ze allemaal verschillende gerechten kiezen?
         

0,0246
           
14. Gooi zes dobbelstenen.
Vermenigvuldig de aantallen ogen met elkaar.
Hoe groot is de kans dat er 36 uitkomt?
         

0,0061
15. examenvraagstuk HAVO wiskunde A, 1989

Bij een helderziendheidstest wordt een stapel van 25 kaarten gebruikt, waarin elk van onderstaande kaarten vijf keer voorkomt.
           
 

           
  De kaarten worden goed geschud en vervolgens worden er drie kaarten tegelijk uit de stapel getrokken. De proefpersonen moeten voorspellen welke kaarten getrokken zullen worden.

Een proefpersoon raadt op goed geluk dat er 2 sterren en 1 cirkel worden getrokken.
Bereken de kans dat zijn 'voorspelling' uitkomt.
         

0,0282
           
         

© h.hofstede (h.hofstede@hogeland.nl)