| |
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
| 1 |
Een schip vol olie is gestrand in zee en door
een gat in de romp loopt er olie de zee in.
Per minuut stroomt 50 liter olie de zee in, te beginnen op
tijdstip t = 0
Die olie vormt op het zeewater een grote vlek. Neem aan dat die
vlek (bij benadering) cirkelvormig is. De dikte van de olielaag
is gelijk aan 2 mm. Neem verder aan dat alle olie zich direct
tot een cirkelvormige vlek met dikte 2 mm verspreidt.
Voor de straal van die cirkelvormige olievlek geldt dan ongeveer
r(t) = 2,82√t
met r in meters en t in minuten. |
| |
|
|
|
|
| |
a. |
Leg uit waar deze formule vandaan
komt. |
| |
|
|
|
|
| |
b. |
Onderzoek hoe snel de straal van de
olievlek groeit (in m/min) op tijdstip t = 20 min.
|
| |
|
|
|
|
| 2. |
Met een cilinder gevuld met helium
kun je ballonnen opblazen. Per seconde perst de cilinder 0,2
liter helium in een ballon. Neem aan dat de ballon op elk moment
bolvormig is. De inhoud van een bol is gelijk aan
4/3pr3.
Op t = 0 begint men een ballon op te blazen.
Voor de diameter (d in cm) van die ballon geldt (met t
de tijd in seconden): |
| |
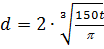 |
| |
|
|
|
|
| |
a. |
Toon deze formule aan. |
| |
|
|
|
|
| |
b. |
Hoe snel (in cm/sec) neemt de
diameter toe op t = 2? |
| |
|
|
|
|
| |
|
|
|
|
| 3. |
Een punt P beweegt over de x-as,
waarbij voor de x-coördinaat van P geldt: xP
= 2t3 - 10t2 + 6t - 4 |
| |
|
|
|
|
| |
a. |
Beweegt het punt op t = 2
naar rechts of naar links? |
| |
|
|
|
|
| |
b. |
Wanneer staat het punt stil? |
| |
|
|
|
|
| |
c. |
Met welke snelheid passeert P de
oorsprong? |
| |
|
|
|
|
| |
|
| 4. |
Examenvraagstuk HAVO Wiskunde B,
2004 De luchtdruk in de atmosfeer
is afhankelijk van de hoogte boven het zeeniveau.
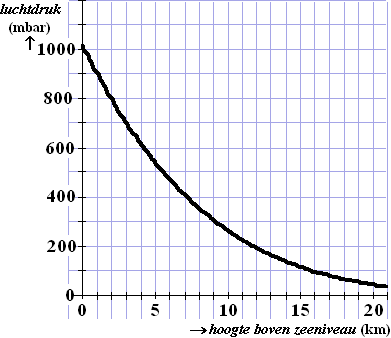
De grafiek hieronder geeft het verband weer tussen de luchtdruk in
millibar (mbar) en de hoogte boven het zeeniveau in kilometer (km).
De luchtdruk op zeeniveau is gelijk aan 1014 mbar. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
In deze figuur is te zien dat
de luchtdruk afneemt als de hoogte toeneemt.
Er is een hoogte waarop de snelheid waarmee de luchtdruk afneemt gelijk
is aan 5 mbar per 100 meter. |
| |
|
|
|
|
| |
a. |
Onderzoek met behulp van de
figuur op welke hoogte dit het geval is.
Licht je werkwijze toe. |
| |
|
|
|
|
| |
Voor het verband tussen de
luchtdruk D (in mbar) en de hoogte h (in km) geldt bij benadering
de formule:
D = 1014 • (-0,0226h + 1)5,26
Met behulp van differentiëren is de snelheid (in mbar/km) te
berekenen waarmee de luchtdruk verandert. |
| |
|
|
|
|
| |
b. |
Bereken deze snelheid op een hoogte van 3 km.
Rond je antwoord af op één decimaal. |
| |
|
|
|
|
| |
|
|
|
|
| 5. |
Twee
politieagenten zitten in hun patrouillewagen langs een lange
rechte weg. Opeens komt er met enorme vaart een auto
langsgereden. Hij rijdt met constante, maar veel te hoge
snelheid.
De agenten schrikken wakker en zetten de achtervolging in.
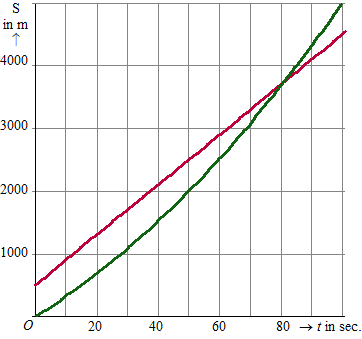
In onderstaande grafiek zie je de afstand van de politiewagen én
de afstand van de overtreder, gemeten vanaf het punt waar de
politieauto stond, als functie van de tijd.
t is de tijd in seconden met t = 0 het
moment dat de politieauto begint te rijden.
S is de afstand in meters. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Voor de
overtreder blijkt te gelden S(t) = 40t + 500 |
| |
|
|
|
|
| |
a. |
Hoeveel km/uur rijdt de
overtreder? |
|
|
| |
|
|
|
|
| |
b. |
Bepaal met
de grafiek op welk moment de overtreder en de politieauto even
hard reden. |
| |
|
|
|
|
| |
Voor de
politieauto blijkt te gelden: S = 0,2t2
+ 30t |
| |
|
|
|
|
| |
c. |
Teken een toenamendiagram voor de politieauto voor t tussen 0 en
100 met stapgrootte 20. |
| |
|
|
|
|
| |
d. |
Op welk
moment haalt de politieauto de overtreder in? Geef je antwoord
in twee decimalen nauwkeurig. |
| |
|
|
|
|
| |
|
|
|
|
| 6. |
Men laat
een reservoir met daarin 8000 liter water leegstromen door een
kraan aan de onderkant open te zetten.
Voor de hoeveelheid water in het reservoir geldt V = 8000
• (1 - t/270)2 met
t de tijd in minuten vanaf het moment van openzetten en V
het watervolume in liters. |
| |
|
|
|
|
| |
a. |
Hoe lang
duurt het voordat het reservoir leeg is? |
| |
|
|
|
|
| |
b. |
Hoeveel
liter stroomt er per seconde op t = 30 uit het reservoir? |
| |
|
|
|
|
| |
|
|
|
|
|
7. |
Men laat een reservoir met daarin 8000 liter water leegstromen
door een kraan aan de onderkant open te zetten.
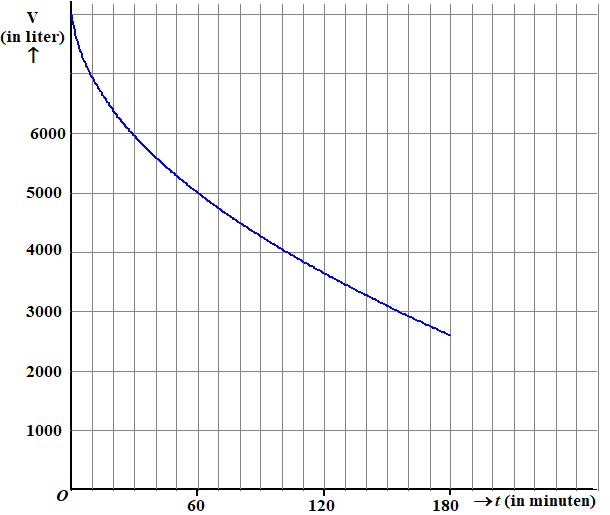
Voor de hoeveelheid water in het reservoir geldt V = 8300
- 300√(2t
+ 1)
Daarin is t de tijd in minuten vanaf het moment van
openzetten en V het watervolume in liters.
Hieronder
zie je een grafiek van V. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
a. |
Bereken het differentiequotiënt van V op interval [0, 75] en
leg duidelijk uit wat dit getal voorstelt. |
| |
|
|
|
|
| |
Op een gegeven moment berekent een medewerker dat het vat, vanaf
het begin gerekend, een gemiddelde leegstroomsnelheid van 50
liter per minuut heeft gehad. |
| |
|
|
|
|
| |
b. |
Onderzoek m.b.v. de grafiek hoeveel water er op dat moment
nog in het vat zit |
| |
|
|
|
|
| |
Men wil graag weten wat de uitstroomsnelheid (in liter/minuut)
op tijdstip t = 120 nog is. |
| |
|
|
|
|
| |
c. |
Benader deze snelheid m.b.v. de grafiek. |
| |
|
|
|
|
| |
Het vat stroomt steeds langzamer leeg.
Men heeft echter ook de mogelijkheid om de uitstroomopening niet
open te laten, maar om er een pomp op aan te sluiten.
Deze pomp haalt per minuut constant 16 liter water uit het
vat en men besluit om op t = 180 de pomp aan te zetten,
omdat het vat op dat moment ook ongeveer leegliep met een
snelheid van 16 liter/minuut. |
| |
|
|
|
|
| |
d. |
Bereken die snelheid op t = 180 in twee decimalen
nauwkeurig. |
| |
|
|
|
|
| |
Door de pomp aan te sluiten is het vat eerder leeg dan wanneer
het alleen via de uitstroomopening zou leeglopen. |
| |
|
|
|
|
| |
e. |
Bereken algebraïsch hoeveel tijdwinst men boekt door de pomp
op t = 180 aan te zetten. Geef je antwoord in minuten en
seconden nauwkeurig. |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |