 |
|
ę
h.hofstede (h.hofstede@hogeland.nl) |
|
Andere projecties. |
| |
|
|
|
| |
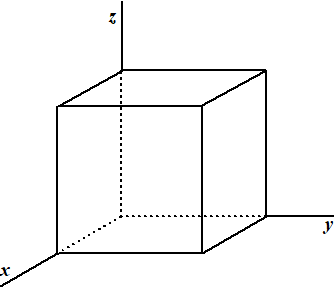
| De meest gebruikelijke manier om
een ruimtelijk assenstelsel (met een x-as en een y-as en
een z-as) te tekenen is om de y-as en de z-as in
het vlak van het papier loodrecht op elkaar te tekenen, en de x-as
een stompe hoek met de y-as te laten maken, zoals hiernaast. |
 |
| |
|
|
|
|
Militaire projectie. |
|
| |
|
|
|
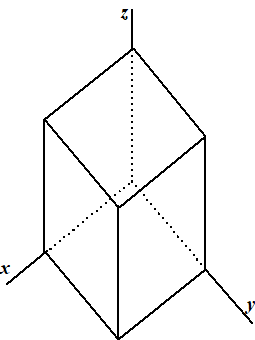
| Bij de militaire
projectie worden de x-as en de y-as loodrecht op
elkaar in het vlak van het papier getekend, maar wel verdraaid ten
opzichte van de verticaal. De z-as wordt vervolgens
verticaal getekend. De hoeveelheid draaiing kun je vrij kiezen. |
 |
| |
|
|
|
|
Loodrechte projecties. |
| |
|
|
|
|
1. Isometrische
projectie. |
| |
|
|
|
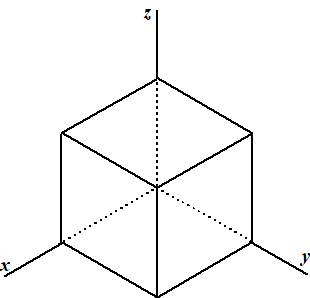
In de isometrische
projectie maken de drie assen hoeken van 120║ met elkaar. De eenheden op
de drie assen zijn hier even groot.
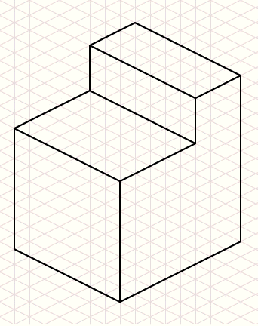
Om figuren in isometrische projectie te tekenen kun je handig gebruik
maken van isometrisch papier. Dat is papier dat bestaat uit
allemaal gelijkzijdige driehoekjes. Hieronder zie je een voorbeeld. |
 |
| |
|
|
|
 |
| |
|
|
|
|
2. Ingenieursprojectie. |
| |
|
|
|
Bij de
ingenieursprojectie maken de y-as en de z-as een hoek van
97,2║ met elkaar en deelt de x-as de hoek tussen y-as en
z-as doormidden. (Dat geeft dus twee hoeken van 131,4║)
De lengteverhoudingen zijn hier 1 : 2 : 2. |
 |
| |
|
|
|
| |
|
|
|
Het algemene geval.
Bij beide vorige projecties (en eigenlijk bij alle loodrechte
projecties) hebben we te maken met drie assen (x, y,
z) die loodrecht op elkaar staan, en een vlak T (het tafereel)
waarop de figuur geprojecteerd moet worden.
In het algemeen ziet dat er zˇ uit: |
| |
 |
| |
|
|
|
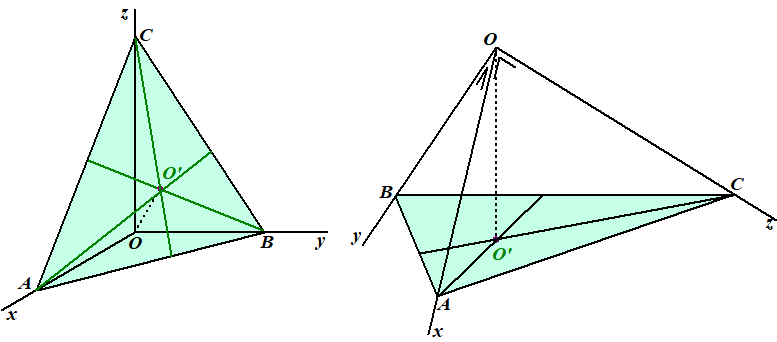
Hier staat twee keer
dezelfde tekening, met het groene tafereel ABC.
Het blijkt dat O' het hoogtepunt is van driehoek ABC.
Dat is logisch, want: |
| |
AO staat loodrecht op vlak
OBC dus loodrecht op alle richtingen van dat vlak, dus AO
staat loodrecht op BC |
| |
OO' staat loodrecht op
vlak ABC dus loodrecht op alle richtingen van dat vlak, dus OO'
staat loodrecht op BC |
| |
BC staat
loodrecht op AO en op OO' dus op het hele vlak AOO' |
| |
Dus BC staat
loodrecht op AO' dus AO' is hoogtelijn van driehoek ABC |
| |
Op dezelfde manier
zijn ook CO' en BO' hoogtelijnen van ABC. |
| q.e.d. |
|
|
|
| |
|
|
|
In de projectie worden de lijnen
OA, OB en OC verkort op het tafereel afgebeeld als
O'A, O'B en O'C.
De verkortingsfactoren v zijn dan: vx
= O'A/OA en vy
= O'B/OB en vz
= O'C/OC
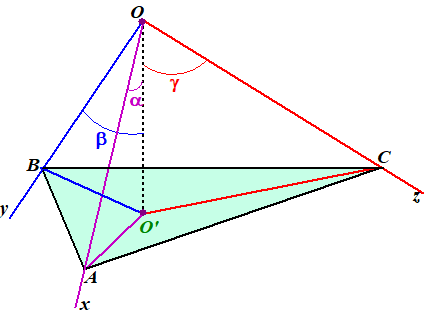
Maar dat zijn precies de sinussen van de drie hoeken
α,
β en
γ die OO' maakt
met de assen!! Kijk maar, een simpel gevalletje van overstaande/aanliggende
zijden: |
| |
|
|
|
|
 |
| |
|
|
|
| Nou is OO' een vector, en daarvan
bekijken we de drie hoeken
(α,
β en
γ) die die vector met
drie loodrecht op elkaar staande assen maakt. Daar ken ik toevallig een
leuke stelling voor! |
| |
|
|
|
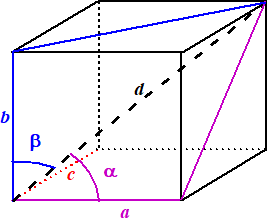
Kijk naar de figuur
hiernaast (een balk). De diagonaal d maakt drie hoeken met de
zijden a en b en c
Omdat ik alleen iets over de hoeken wil ontdekken, neem ik d = 1
(ik teken gewoon met de richting van d een lengte 1, en
daarna a, b en c).
Ruimtelijk Pythagoras zegt dan dat a2 + b2
+ c2 = 1
Maar in de figuur hiernaast zie je dat cosα
= a/d = a/1 =
a
en cosβ = b/d
= b/1 = b en cosγ
= c/d = c/1
= c
Dat geeft cos2α
+ cos2β + cos2γ
= 1 |
 |
Omdat cos2x
= 1 - sin2x geldt dus :
1 - sin2α + 1 - sin2β
+ 1 - sin2γ = 1
sin2α + sin2β
+ sin2γ = 2
ofwel: |
| |
|
|
|
|
|
| |
|
|
|
Bedenk dat deze regel altijd
geldt, ongeacht van de keuze van het tafereel. (Een speciaal geval is
als het tafereel loodrecht op een co÷rdinaat-as staat, dan is de factor
v in die richting 0, en in de andere twee richtingen is v =
1)
Even kijken wat dat tot gevolgen heeft voor de twee projecties
hierboven: |
| |
|
|
|
|
1. Isometrische projectie. |
| |
|
|
|
Nu is driehoek ABC gelijkzijdig.
dus de verkortingsfactor is voor alle zijden gelijk,
Dus v2 + v2 + v2
= 2 dus v = 1/3√6
(≈ 0,82) |
| |
|
|
|
|
2. Ingenieursprojectie. |
| |
|
|
|
Als de verkortingsfactor in de
x-richting gelijk is aan v, dan zijn die factoren in de
y- en z-richting beiden gelijk aan 2v
Dat geeft v2 + (2v)2 + (2v)2
= 9v2 = 2
Dus v = 1/3√2
(≈ 0,47) |
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
| 1. |
examenvraagstuk HAVO Wiskunde B, 1989. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Van de kerk op de foto wordt de toren
nader bekeken. De plattegrond van deze toren is een vierkant van 6
bij 6 m. Het dak wordt gevormd door vier even grote, ruitvormige
dakdelen. De laagste hoekpunten van de dakdelen liggen op een hoogte
van 18 m. De top ligt op een hoogte van 26 m. De vier hoekpunten van
het dak liggen op 22 m hoogte, elk op de symmetrieas van een van de
zijmuren. In de volgende tekening is een begin gemaakt met een
tekening van de toren in zogenaamde ingenieursprojectie. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Voltooi de projectiefiguur
van de toren. Teken de lijnen die in werkelijkheid niet zichtbaar
zijn als stippellijnen. |
| |
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|