De Hoofdstelling.

© h.hofstede (h.hofstede@hogeland.nl)


afgeleide benaderen
differentiëren van machtsfuncties
Na alle methodes om een oppervlakte te berekenen met rechthoekjes, lijsten, Riemann-sommen en de Grafische rekenmachine knaagt er bij de echte wiskundige natuurlijk de vraag:
Kan het ook algebraïsch?
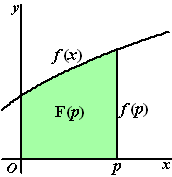
Neem de oppervlakte onder de één of andere grafiek van functie f(x)
Bereken die oppervlakte vanaf x = 0 tot  x = p
Laten we de uitkomst F(p) noemen., dus:

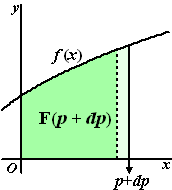
Om te bekijken hoe F(p) van p afhangt, gaan we p een klein beetje groter maken, en kijken we wat dat verandert aan F(p).
Hiernaast hebben we p veranderd in p + dp  en dat heeft tot effect dat er aan de oppervlakte het lichtgroene deel wordt toegevoegd.

Je ziet dat geldt:  F(p + dp) = F(p) + lichtgroene deel.

Maar als we dp maar klein genoeg kiezen, dan is dat lichtgroene deel ongeveer een rechthoek met breedte dp en lengte f(p)
De oppervlakte daarvan is  f(p) • dp

Kennelijk geldt:     F(p + dp) = F(p) + f(p) • dp
Doe F(p) naar de linkerkant, en deel daarna alles door dp, dan vind je:
En daar aan de linkerkant staat een oude bekende!  De Afgeleide!!!
Conclusie:

F' =  f
Kunnen we dat ook zonder al die moeilijke formules beredeneren?
We kunnen het proberen:
F' is de afgeleide van F, en de afgeleide van een functie geeft aan hoe snel die functie verandert.
Dus F'  zegt hoe snel de oppervlakte verandert als p toeneemt.
f is de hoogte van de grafiek op het punt p waar je nu bent.
Dus de regel F' = f is eigenlijk precies hetzelfde als:
Hoe snel de oppervlakte verandert  =  Hoe hoog de grafiek is

Hopelijk vind je deze regel logisch als je dat extra lichtgroene rechthoekje in gedachten hebt. Immers als f groter is, dan ligt de grafiek hoger, dus is de lengte van het extra lichtgroene rechthoekje ook groter, dus groeit F sneller.

Hoe passen we dit toe?

De vraag is eigenlijk:  "Kunnen we F vinden als f  gegeven is?"
Neem bijvoorbeeld  f(x) = 3x2  dan is dus de vraag:  "Voor welke functie F geldt dat  F' = 3x2?"
Ofwel; je hebt een functie F, en als je hem gaat differentiëren dan is 3x2 de uitkomst.
Om die functie F te vinden moet je dus eigenlijk  "TERUG-DIFFERENTIËREN"
Dat is niet een officiële wiskundige term; wiskundigen noemen het "primitiveren", en die gezochte functie F heet de "primitieve" van f  (net het omgekeerde van de afgeleide).

Heb je hem intussen al gevonden?
De functie waarvan de afgeleide gelijk is aan 3x2   is natuurlijk F(x) = x3 .
1. Zoek (door gewoon een beetje te proberen) de primitieven F  van de volgende functies  f:
a. f(x) = 2x d.   f(x) = 5
b. f(x) =  x2 e.   f(x) = 3x2
c. f(x) = 6x2 f.    f(x) = 2x3 
Een Complicatie! Er klopt iets niet!!
In het bovenstaande verhaal hebben we steeds gesteld dat F(p) de oppervlakte is onder de grafiek van f(x) tussen x = 0 en x = p.  Maar daarna zijn we alleen maar bezig geweest met hoe snel F verandert aan de rechterkant bij de bovengrens x = p. Die x = 0 is nergens meer gebruikt.......

Is dat erg dan?

Nou ja......eigenlijk WEL!
Als je in het hele verhaal hierboven de 0 vervangt door bijvoorbeeld -2, dan VERANDERT ER NIETS! We vinden dezelfde primitieve F. Toch is de oppervlakte dan anders!!!!!!!

Hoe zit dat?  Hebben we een fout gemaakt?

Nou nee, gelukkig hebben we in ons verhaal dat leidde tot  F' = f geen fout gemaakt. Dat klopt inderdaad en is ook geheel onafhankelijk van die ondergrens. Dat komt omdat we bij het primitiveren iets zijn vergeten.
We vonden dat de primitieve van 3x2 gelijk was aan  x3  omdat de afgeleide van x3 gelijk is aan 3x2
Maar er zijn méér functies waarvan de afgeleide gelijk is aan 3x2 .
Neem maar x3 + 1 of x3 + 2  of  x3 + 3  of  x3 + 4  of x3 - 1  of....... Die geven allemaal dezelfde afgeleide.
Zo'n constant getal kun je altijd aan de primitieve toevoegen want bij het differentiëren verdwijnt dat toch.
Eigenlijk hadden we moeten zeggen dat  F(x) = x3 + c  met c een constant getal.
Primitieven zijn op een constante na bepaald.

Hoe lossen we dat op?

Helaas is het niet zo dat als de ondergrens nul is, dat dan ook c gelijk aan nul is.
Kijk bijvoorbeeld naar de oppervlakte onder de grafiek van y = sinx tussen x = 0 en x = π.
De primitieve van  f(x) = sinx  is  F(x) = -cosx + c  (ga maar na door te differentiëren)

Als je voor de oppervlakte tussen 0 en π neemt c = 0 dan geeft dat  F(π) = -cosπ = --1 = 1

Maar als je invoert  Y1  = sin(X) en dan  CALC - integraal dan vind je dat de oppervlakte gelijk is aan 2.
Dat klopt dus niet!

Er is voor dit probleem een prachtige eenvoudige oplossing, en die is:

Het doet er allemaal niet toe!

Omdat we steeds de oppervlakte tussen twee x-grenzen willen weten maakt het niets uit wat c is.
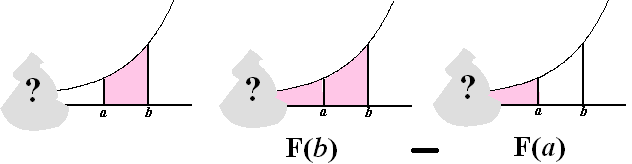
Stel dat we in een ideale wiskundewereld leven en precies hebben gevonden welke c bij welke ondergrens hoort. Als we dan de oppervlakte tussen x = a  en x = b willen uitrekenen, dan gelden de volgende plaatjes (er staat expres geen y-as bij omdat die er niet toe doet, en het grijze gedeelte aan de linkerkant is een groot vraagteken): 

De oppervlakte tussen twee grenzen a en b in is altijd gelijk aan F(b) - F(a)
En dan doet die constante c  in de F er helemaal niet meer toe.
Immers als je een gevonden F vervangt door F + c dan geeft dat:
F(b) - F(a)  wordt  (F(b) + c) - (F(a) + c) = F(b) + c - F(a) - c  =  F(b) - F(a)
Precies weer dezelfde oppervlakte! Die c's vallen gewoon tegen elkaar weg.

We noteren dit voortaan als volgt:
Als je het zo opschrijft dan is de waarde van c onbelangrijk. Ik stel voor om bij het primitiveren voor het gemak steeds maar c = 0 te nemen (dus eigenlijk gewoon c vergeten). Maar ja, als je graag hebt c = 4  of  c = √2  of zoiets:  ga vooral je gang, maar je maakt het jezelf  alleen maar moeilijk.
2. Schrijf als één integraal:
a. b.
3. Leg duidelijk uit waarom voor kleine dp geldt dat:
   

 
4.
Hiernaast staat een gebied gekleurd, dat aan de rechterkant wordt begrensd door de lijn x = p en aan de bovenkant door de lijn y = 3 + 0,75x.
De twee andere grenzen zijn de x-as en de y-as.

De oppervlakte A van dit gebied hangt natuurlijk af van p, dus is  A(p).

   
a. Stel een formule op voor A(p) door het gebied in een rechthoek en een driehoek te verdelen.
   
b. Hoe kun je A' (p) in de figuur terugvinden?
 

© h.hofstede (h.hofstede@hogeland.nl)