| In deze les is de verzameling die
we bestuderen die van de punten in het platte vlak. Die kun je door twee
coördinaten (x, y) weergeven. We zullen in dat platte vlak
groepen van afbeeldingen bekijken die bepaalde eigenschappen van die
punten en de lijnstukken ertussen (afstanden, hoeken e.d.) onveranderd
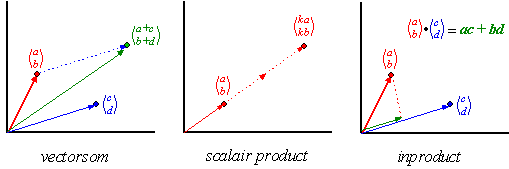
laten. Als je een punt als een vector ziet, dan kun je met die vectoren drie verschillende dingen uitvoeren. |
|||||||||
 |
|||||||||
|
Denk erom dat die eerste twee als resultaat weer een vector hebben, maar dat die derde als resultaat een getal heeft (in dit geval de lengte van de groene en blauwe vectoren met elkaar vermenigvuldigd). |
|||||||||
|
Isometrieën. |
|||||||||
| We gaan nu
afbeeldingen bekijken die het platte vlak op zichzelf afbeelden
(bijecties; één-op-één) met als voorwaarde dat afstanden ongewijzigd
blijven. Dus de afstand tussen twee punten A en B is hetzelfde als de
afstand tussen hun beeldpunten A' en B'. Zo'n afbeelding heet een
isometrie. Als bovendien de oorsprong óók nog op zichzelf wordt
afgebeeld, dan heet zo'n afbeelding een orthogonale afbeelding.
Verder heet een punt dat op zichzelf wordt afgebeeld (waarvoor dus
A' = A) een dekpunt. Voorbeelden van isometrieën:
|
|||||||||
|
|||||||||
| Bewijs in
drie stappen. (we hebben het eventjes niet over het "flauwe" geval van de identiteit: de afbeelding waarbij er niets gebeurt) Stap 1. Als een isometrie precies twee dekpunten heeft, dan is het een spiegeling in de lijn door die twee punten. |
|||||||||
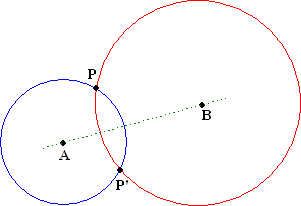
| Dat kun je in het
plaatje hiernaast zien. Als A en B dekpunten zijn, dan
moeten alle afstanden van andere punten tot A en B gelijk blijven
(anders is het geen isometrie). Kies een willekeurig punt P; dan moet
dus gelden AP = AP', dus moet P' op de blauwe cirkel hiernaast
liggen. Maar ook moet gelden dat BP' = BP dus moet P' ook op de rode cirkel hiernaast liggen. Omdat P' niet gelijk kan zijn aan P (er waren immers maar 2 dekpunten) moet P' wel het punt dat hiernaast is getekend zijn. Dat is inderdaad P gespiegeld in de lijn door A en B. |
|
||||||||
| Stap 2. Een orthogonale afbeelding is een rotatie, eventueel gevolgd door een spiegeling in de x-as. |
|||||||||
|
|
|||||||||
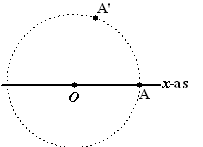
| Kies een willekeurig
punt A op de x-as. Kies een willekeurige orthogonale afbeelding f waardoor A wordt afgebeeld op A'. Bij een orthogonale afbeelding blijft O op zijn plaats, en omdat afstanden gelijk moeten blijven moet dus gelden OA = OA'. Dat betekent dat A' ergens op een cirkel met middelpunt O en straal OA moet liggen (zie hiernaast) Maar dat betekent dat A' uit A te krijgen is door één of andere rotatie R om de oorsprong: A' = R(A) f(A) = A' = R(A) pas daar nu de inverse rotatie op toe: R-1o f(A) = R-1(R(A)) = A Dat betekent dat R-1f twee dekpunten heeft: A en de oorsprong, dus volgens stap 1 hierboven is R-1f een spiegeling in de x-as (of de identiteit; in dat geval is f gewoon de rotatie R). Dan is RR-1f = f een spiegeling in de x-as gevolgd door een rotatie R. |
 |
||||||||
| Stap 3. Neem nu een nieuwe willekeurige isometrie f en noem het beeld van de oorsprong f(O) = O'. Neem nu de translatie T over vector OO' T-1 o f laat dan O op zijn plaats, dus is een orthogonale afbeelding, dus is volgens stap 2 hierboven te schrijven als een rotatie, gevolgd door evt een spiegeling in de x-as. Dan is T o (T-1 o f) = f dus een rotatie gevolgd door evt een spiegeling in de x-as plus een translatie. q.e.d. samengevat: |
|||||||||
|
|||||||||
| Volgende Stelling: | |||||||||
|
|||||||||
| Bewijs (uit
het ongerijmde) Stel dat er verschillende T en φ zijn zodat T1 o φ1 = T2 o φ2 Omdat T en φ bijecties zijn bestaan hun inversen, dus mogen we daar wel mee vermenigvuldigen: Eerst met T2-1 vermenigvuldigen T2-1o T1 o φ1 = T2-1 o T2 o φ2 = φ2 En dan met φ1-1 vermenigvuldigen: T2-1 o T1 o φ1 o φ1-1 = T2-1 o T1 = φ2 o φ1-1 Links staat een translatie, rechts een orthogonale afbeelding. Maar de enige translatie die gelijk kan zijn aan een orthogonale afbeelding is de translatie met vector NUL: de identiteit. Rechts en links hierboven staat dus twee keer de identiteit!! Maar als T2-1 o T1 en φ2 o φ1-1 de identiteit zijn, dan is T2 = T1 en φ1 = φ2. q.e.d. |
|||||||||
| Een belangrijk gevolg
van het feit dat elke isometrie als T o f te
schrijven is, is dat elke isometrie een bijectie is, immers T en
φ
zijn beiden bijecties, dus hun
samenstelling ook. Toen we begonnen over isometrieën stelden we al dat
het bijecties zijn, maar we zien nu dat dat geen eis is, maar dat dat
gewoon volgt uit hun eigenschappen. En dan nu waar het eigenlijk allemaal om ging: |
|||||||||
|
|||||||||
| Bewijs: • we zagen al dat een isometrie is opgebouwd uit bijecties, dus zelf ook een bijectie is. • de identiteit is een isometrie en fungeert als eenheidselement e • als een bijectie afstanden bewaart doet zijn inverse dat ook, dus is dat ook een isometrie. (Het bewijs voor O als ondergroep gaat precies zo) q.e.d. |
|||||||||
|
De ondergroep O van de
orthogonale afbeeldingen. Zoals we al zagen is elke orthogonale afbeelding weer te geven door een rotatie plus eventueel een spiegeling in de x-as. We kunnen zo'n orthogonale afbeelding in het algemeen schrijven als O = Rα o Sx (een draaiing om de oorsprong over een hoek α en een spiegeling in de x-as) Deze orthogonale afbeeldingen zijn samen eigenlijk niets anders dan de symmetriegroep van de eenheidscirkel. (net zoals we al eerder de symmetriegroepen V4 van de ruit en D4 van het vierkant vonden). Ze vertegenwoordigen alle afbeeldingen waarbij de eenheidscirkel met zijn beeld samenvalt. Immers wat kun je nou helemaal met zo'n eenheidscirkel doen? Je kunt hem draaien over een aantal graden (rotatie) of je kunt hem omklappen zodat de oriëntatie verandert (spiegeling). That's All Folks! |
|||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||