| |
 |
| Grafieken. |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
| Een grafiek is een erg mooie
manier om een "plaatje" te maken van een tabel met getallen. |
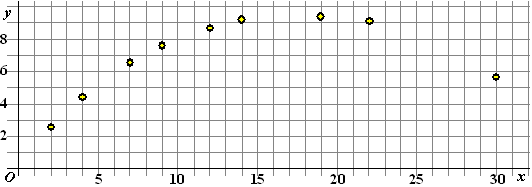
Neem de tabel hiernaast. Daar
staat het één of andere getal P (ik zeg expres niet wat het voorstelt)
en elke keer het bijbehorende getal Q.
Als je nu het getal P elke keer x noemt en het getal Q
allemaal y, dan staan daar negen paren (P, Q) = (x, y)
en die kun je in een assenstelsel tekenen. Kijk maar: |
|
P |
2 |
4 |
7 |
9 |
12 |
14 |
19 |
22 |
30 |
|
Q |
2,7 |
4,5 |
6,6 |
7,7 |
8,8 |
9,2 |
9,3 |
9,1 |
5,8 |
|
| |
|
|
|
|
 |
| |
|
|
|
Maar daarbij komen er
toch een aantal vragen naar boven. Tenminste bij mij wel....
Hier is de eerste:
Wat is x en wat is y
?
Tja, dat is niet altijd zomaar duidelijk. |
Je zou de grafiek
hierboven bijvoorbeeld net zo goed kunnen tekenen met P op de y-as
en Q op de x-as. In sommige gevallen is er wel iets over te
zeggen.
1. Als in de opgave erbij staat wat x en wat y
moeten zijn.
Soms heb je niets te kiezen maar zegt degene die de opgave maakte (de
auteur van het boek, of jouw docent(e) wiskunde) gewoon botweg wat je
moet doen. Meestal doen ze dat nog wel redelijk netjes, en staat er: |
 |
| |
|
|
|
|
| |
|
|
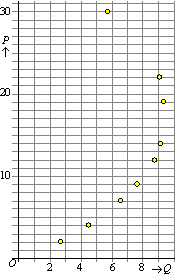
Als er bij de
oorspronkelijke tabel met P en Q zou staan "Zet Q uit tegen P" dan
moet dus Q op de y-as en P op de x-as en krijg je de
grafiek hierboven. maar als er staat "Zet P uit tegen Q" dan gaat het
net andersom en krijg je de grafiek hiernaast.
|
2. Oorzaak en
Gevolg.
Soms is duidelijk één van beiden de oorzaak en de andere het
gevolg ervan. We noemen het ook wel de onafhankelijke variabele
(oorzaak) en de afhankelijke variabele (gevolg). De
onafhankelijke variabele is degene waar je mee begint, waar je als
experimenteerder vaak een waarde voor kiest. De afhankelijke variabele
is wat je daarbij meet voor de andere grootheid. In zulke gevallen kies
je: |
|
|
|
onafhankelijk (oorzaak): x-as
afhankelijk (gevolg): y -as |
|
| |
|
|
|
Voorbeeld.
Stel dat ik een tabel met meetwaarden heb van een aantal keer de
temperatuur (T) en de bijbehorende luchtdruk (P), dan hangt er soms van
af hoe mijn experiment is geweest. Kijk maar naar de volgende drie
gevallen: |
| 1. |
Ik ben in een
afgesloten kamer gaan zitten en heb langzaam de thermostaat omhoog
gedraaid. Bij een aantal temperaturen heb ik steeds de luchtdruk
gemeten.
In dit geval is degene waar je mee begint de temperatuur. Je stelt zélf
een aantal temperaturen in en meet elke keer de bijbehorende luchtdruk.
Ik zou daarom de temperatuur als onafhankelijke variabele kiezen (x-as)
en de luchtdruk als afhankelijke (y-as) |
| 2. |
Onder een glazen
stolp zuig ik langzaam met een pomp de lucht weg.
Daardoor wordt de luchtdruk eronder steeds lager en bij een aantal van
die luchtdrukken noteer ik de temperatuur.
In dit geval begin je met een luchtdruk in te stellen en meet je daarna
de daarbij horende temperatuur. Ik zou daarom nu de luchtdruk op de x-as
zetten (begin je mee) en de temperatuur op de y-as |
| 3. |
Ik laat een
luchtballon langzaam opstijgen en meet elke 100 meter de temperatuur en
de luchtdruk.
In dit geval.... weet ik het niet! Doe maar wat!!! |
| |
|
|
|
|
nog twee vage tips: |
|
- |
Vaak wordt gemeten hoe een bepaalde grootheid
in de loop van de tijd verandert. In zulke gevallen zou ik de tijd
op de x-as zetten (maar weer niet als je bijvoorbeeld iemands
reactievermogen meet en het aantal glazen wijn dat hij heeft gedronken,
dan zou ik de tijd toch op de y-as zetten. Jij ook?) |
|
- |
De onafhankelijke variabele wordt vaak door de
onderzoeker ingesteld en bestaat vaak uit mooie gehele waarden. De
afhankelijke is resultaat van een meting en komt vaak niet zo mooi uit.
In het allereerste voorbeeld van deze les zou ik daarom, zonder verdere
informatie, P op de x-as zetten (mooie getallen) en Q op de y-as. |
| |
|
|
|
|
Moet ik de stippen met lijntjes
verbinden of niet? |
| |
|
|
|
Soms wel, soms niet.
Dat hangt er van af of de gegevens van de x-as en van de y-as
discreet of continu zijn. Daar wordt het
volgende mee bedoeld: |
| • |
Gegevens zijn
discreet als ze bestaan uit "losse", "alleenstaande" getallen,
waarbij de tussenliggende waarden niet allemaal mogelijk zijn. Bekijk
bijvoorbeeld het aantal glazen bier dat ik in een week in de kroeg koop.
Dat kan gelijk zijn aan 8 of aan 15, maar het is niet gelijk aan 14,672
dat is onmogelijk. |
| • |
Gegevens zijn
continu als de tussenliggende waarden in principe ook mogelijk
zijn. Bekijk bijvoorbeeld het aantal liter bier dat ik in een week
drink. Dat kan gelijk zijn aan 20 of aan 3. Maar het kan ook best
16,2354 zijn. In principe zijn alle tussenliggende waarden mogelijk
(alhoewel we daarvoor vaak niet nauwkeurig genoeg kunnen meten; daarom
staat er ook in principe). |
| |
|
|
|
| Om de verschillen
duidelijk te maken vier voorbeelden. |
| |
|
|
|
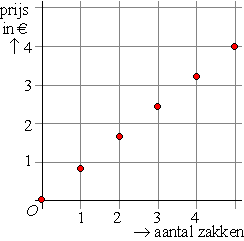
| voorbeeld 1.
Ik koop in de supermarkt een aantal zakken chips voor 0,80 per
stuk. Maak een grafiek van het aantal zakken en het bedrag dat ik
daarvoor moet betalen. |
Ik vind dat het
aantal zakken dat ik koop de oorzaak is van het bedrag dat ik moet
betalen, dus ik kies ervoor om het aantal zakken op de x-as te
zetten en het bedrag op de y-as.
Het aantal zakken kan zijn 0, 1, 2, 3, ... en is dus discreet
Het bedrag kan zijn 0, 0.80, 1.60, 2.40, ... en is ook discreet.
Tussenliggende waarden zijn in beide gevallen niet mogelijk.
Dat geeft de grafiek hiernaast, die dus bestaat uit alleen maar losse
stippen.
Merk nog op dat, alhoewel de stippen op een mooie rechte lijn liggen,
het toch grote onzin is om die lijn te tekenen! Al die punten daar
tussen de rode stippen in bestaan gewoon niet! |
 |
| |
|
|
|
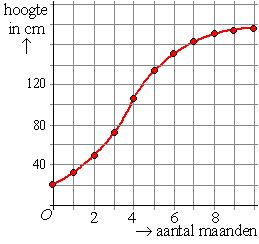
| voorbeeld 2.
Ik plant een boompje in mijn tuin en ik meet elke maand hoe hoog het is. |
| |
|
Omdat de tijd de oorzaak is en de lengte het gevolg kies ik de tijd op
de x-as en de lengte op de y-as.
Stel dat ik de meetpunten (rode stippen) hiernaast heb gevonden.
Dan zou ik daar nu wel zo goed mogelijk een lijn doorheen trekken,
immers het aantal maanden en de hoogte zijn beiden continu: alle
tussenliggende waarden zijn in principe mogelijk. |
 |
| |
|
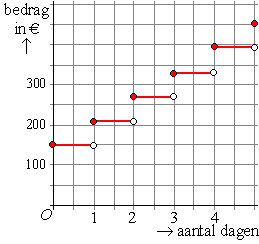
| voorbeeld 3.
Ik moet verhuizen en heb daarvoor een aantal dagen een busje nodig. Het
verhuurbedrijf vraagt een basisbedrag van €150
en daarbovenop nog eens €60 per dag
of gedeelte van een dag. Maak een grafiek tussen de benodigde tijd en
het verschuldigde bedrag. |
Omdat de tijd oorzaak is en het huurbedrag het gevolg zet ik de
benodigde tijd op de x-as en het bedrag op de y-as.
De tijd is continu, maar het bedrag niet, want dat begint bij
€150 en gaat alleen in sprongen van
€60 omhoog. Tussenliggende waarden
kunnen in principe niet voorkomen.
Dat geeft de grafiek hiernaast.
Merk nog even op dat een "open" stip betekent dat het randpunt aan die
kant er niet bij hoort, en een dichte stip dat het randpunt zelf er wel
bij hoort. |
 |
| |
|
|
|
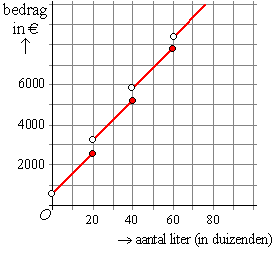
| voorbeeld 4. |
Een benzinestation
bestelt een aantal liters benzine bij een olieraffinaderij. De benzine
moet in tankauto's vervoerd worden.
In zo'n tankauto kan 20000 liter benzine. Het rijden van een auto kost
€600 per auto, en de benzine kost
€0,10 per liter.
Maak een grafiek voor de bestelde hoeveelheid benzine en de prijs. Neem
aan dat elk bedrag mogelijk is. |
| |
|
De oorzaak is de bestelde hoeveelheid benzine (x-as) en
het gevolg de prijs (y-as).
Het aantal liters benzine is duidelijk continu. Kan alles zijn.
Met de prijs is iets vreemds aan de hand. Die is in principe
continu want die hangt af van het aantal liters. Maar de prijs maakt
elke keer een sprong van €600 als er
weer een nieuwe autorit nodig is. Dus zijn sommige waarden toch niet
mogelijk (zoals bijv. €3000)
Dat geeft de grafiek hiernaast. |
 |
| |
|
|
|
Het
schemergebied.....
Vaak maken wij continue variabelen
zelf door onze manier van meten toch discreet.
Neem bijvoorbeeld het gewicht van een aantal leerlingen van de brugklas.
Dat lijkt een continue variabele, immers tussen twee gewichten kunnen
alle tussenliggende waarden in principe ook aangenomen worden. Iemand
kan 62 kg wegen maar ook 63,456 kg of 66,334521 kg
of noem maar op. |
Maar als we de gewichten wegen met
een digitale weegschaal dan zijn opeens die tussenliggende
waarden niet meer mogelijk!
Bij één cijfer achter de komma zijn bijvoorbeeld alleen de
gewichten 126,4 en 145,3 en dergelijke mogelijk, maar niet
meer 126,42 of 145,288897.
Zo maken we eigenlijk in praktijk (bij metingen) alle waarden
discreet. We ronden immers altijd af op een vast aantal cijfers
achter de komma. Zodoende worden getallen die in theorie continu
zijn toch eigenlijk altijd gepresenteerd als discreet. |
 |
|
Bij de opgaven van deze les hoef je daar
niet op te letten. Als een waarde in theorie continu is, mag je
hem ook continu tekenen, en hoef je je niet druk te maken over
de manier waarop hij gemeten wordt. |
| |
|
|
|
| |
|
|
|
|
Zijn er verder nog dingen om op te
letten? |
| |
|
|
|
| We zijn d'r bijna.
Een paar kleinigheden nog....... |
| |
|
|
|
|
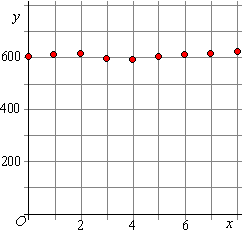
1. |
scheurlijn.
Soms zijn de getallen waar je mee te maken hebt erg groot en variëren ze
helemaal niet zoveel. Als je dan een grafiek tekent, dan zie je
eigenlijk niet zoveel. Neem de volgende tabel links waarvan twee
grafieken zijn gemaakt: |
| |
|
|
|
| |
| x |
y |
0
1
2
3
4
5
6
7
8 |
600
608
611
595
592
598
610
615
621 |
|
 |
 |
| |
|
|
|
| |
In de grafiek in het
midden is niet veel te zien, omdat alle y-waarden zo rond de 600
liggen. Het hele stuk van 0 tot 500 op het grafiekpapier wordt eigenlijk
niet gebruikt.
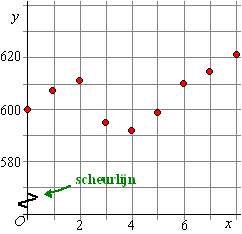
In de rechtergrafiek is dat stuk weggelaten, en is de schaalverdeling
van de y-as uitgerekt. Dat er een stuk is weggelaten geven we aan
met dat zigzagfiguurtje op de y-as. Dat heet een "scheurlijn".
Je ziet dat daardoor de variatie in de y-waarden veel duidelijker
te zien is. |
| |
|
|
|
|
2. |
twee verticale assen. |
|
|
| |
|
|
|
| |
Soms wil je twee
dingen met elkaar vergelijken (vooral hun toename of afname) die erg in
grootte verschillen. |
| |
|
|
|
| |
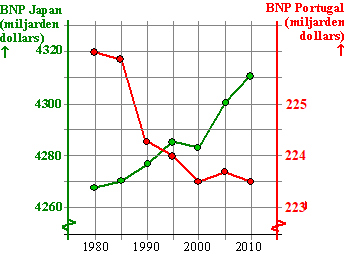
Hiernaast zie je het
BNP (Bruto Nationaal Product) van de landen Japan en Portugal beiden in
miljarden dollars. Omdat dat nogal verschilt is het niet handig om
dezelfde schaalverdeling te gebruiken; dan zou je van Portugal helemaal
niets zien!!
Daarom is Japan getekend met de linker y-as en Portugal met de
rechter y-as. Zo kun je toch de veranderingen vergelijken met
elkaar.
Bedenk wel dat dat snijpunt daar helemaal niets voorstelt!
Bedenk ook dat de hellingen niet met elkaar te vergelijken zijn. Die
"steile" afname van Portugal tussen 1985 en 1990 is bijvoorbeeld
absoluut veel kleiner dan de "lichte" afname van Japan tussen 1995 en
2000....... |
 |
| |
Omdat beide verticale
assen ook nog scheurlijnen hebben is er zelfs niets over de
procentuele toename of afname te zeggen! |
| |
|
|
|
| |
|
|
|
|
|
OPGAVEN |
| |
|
|
|
|
| 1. |
Leg van de
volgende waarden uit of ze (in principe) discreet of continu
zijn: |
| |
|
|
|
| |
a. |
Het cijfer dat je op je volgende
natuurkunde proefwerk gaat halen. |
| |
|
|
|
| |
b. |
De temperatuur die het morgenochtend
als je naar buiten stapt zal zijn. |
| |
|
|
|
| |
c. |
De afstand die iemand elke dag naar
zijn werk toe aflegt. |
| |
|
|
|
| |
d. |
De afstand die iemand volgens zijn
stappenteller op een wandeling heeft afgelegd. |
| |
|
|
|
| |
e. |
Het aantal letters op een bladzijde
van een boek. |
| |
|
|
|
| |
f. |
De tijd die je de komende week zult
doorbrengen achter jouw computer. |
| |
|
|
|
| |
g. |
De totale prijs voor de boodschappen
die iemand in de supermarkt doet. |
| |
|
|
|
| |
|
|
|
| 2. |
Maak grafieken bij de volgende verhaaltjes: |
| |
|
|
|
| |
a. |
Iemand doet mee aan een spelshow en
moet zo snel mogelijk een vastgesteld aantal liters water van
een zwembad naar een aquarium brengen. Hij heeft daarvoor een
kan waar 2 liter water in kan. Elke keer heen en weer lopen plus
de kan legen en vullen kost samen 30 seconden. Hij begint bij
het aquarium met een lege kan. Maak een grafiek voor het
benodigde aantal liters en de tijd die het kost. |
| |
|
|
|
| |
b. |
Een groot aantal
leerlingen gaat op schoolreis. Ze gaan in busjes, en in elke
busje passen 12 leerlingen. Het huren van een busje kost €65,-
Maak een grafiek voor de totale prijs als functie van het aantal
leerlingen. |
| |
|
|
|
| |
c. |
Een supermarkt verkoopt appeltaarten voor
€2,30 per stuk. Maar men heeft vandaag de actie: “3
halen, 2 betalen”. Maak een grafiek van de prijs als functie
van het aantal taarten. |
| |
|
|
|
| |
d. |
Een groot aantal liters
verf moet in blikken worden gegoten. Het zijn blikken van 10
liter. Maak een grafiek voor het aantal benodigde blikken als
functie van het aantal liters verf. |
| |
|
|
|
| |
|
|
|
| 3. |
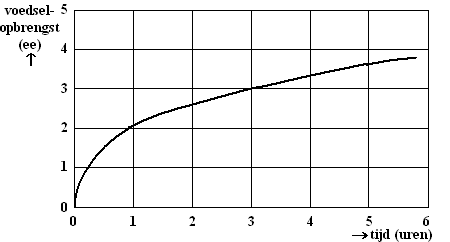
Examenopgave VWO Wiskunde A, 2006.
De meeste roofdieren proberen
iedere dag hun voedsel zo snel mogelijk te vangen. Naarmate meer voedsel
is gevangen wordt het vaak moeilijker om nog nieuw voedsel te vangen. Deze
opgave gaat over het wiskundige model dat daarbij gemaakt kan worden. In
dat model geeft de opbrengstfunctie het verband aan tussen de
hoeveelheid voedsel (de voedselopbrengst) en de tijd die nodig is om die
hoeveelheid voedsel te vangen.
In de volgende figuur is de grafiek getekend van de opbrengstfunctie
voor roofdiersoort A. De voedselopbrengst is uitgedrukt in
energie-eenheden (ee) en de benodigde tijd in uren. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
We bekijken een roofdier van
soort A. Na 0,5 uur heeft dit roofdier een bepaalde hoeveelheid energie
aan voedsel gevangen. Om de dubbele hoeveelheid te vangen is meer dan het
dubbele van 0,5 uur nodig.
Bepaal met behulp van de figuur hoeveel maal
zo groot de daarvoor benodigde tijd is. |
| |
|
|
|
|
| 4. |
Examenopgave VWO
Wiskunde A, 2008.
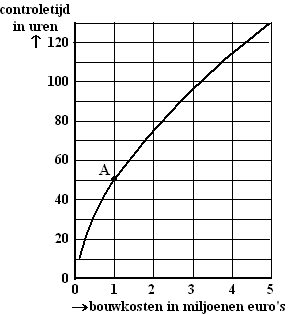
Bij de bouw
van woningen en gebouwen controleert de overheid of de constructie
veilig is. Deze controle kost tijd. Hoe duurder het gebouw, hoe meer
controletijd men denkt nodig te hebben. Het verband tussen
de benodigde controletijd en de bouwkosten is
weergegeven in de volgende figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
Van een
gebouw A zijn de bouwkosten 1 miljoen euro. In de figuur hierboven is af
te lezen dat de controletijd van gebouw A 50 uren
is. Een gebouw B is twee keer zo duur als
gebouw A.
Hoeveel
keer zo groot is de controletijd van gebouw B ten opzichte van de controletijd
van gebouw A? Licht je werkwijze toe. |
| |
|
|
|
|
| |
|
|
|
|
| 5. |
Examenopgave HAVO
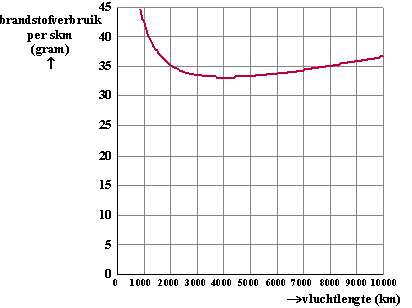
Wiskunde A, 2010. Om het brandstofverbruik van verschillende typen vliegtuigen te kunnen
vergelijken, kijkt men naar het brandstofverbruik per kilometer per
passagier. Men gaat er daarbij van uit dat alle plaatsen (stoelen) in
het vliegtuig bezet zijn.
Dit brandstofverbruik per kilometer per passagier wordt
brandstofverbruik per skm (stoelkilometer) genoemd en wordt
uitgedrukt in gram. |
| |
Men kan
soms brandstof besparen
door zo weinig mogelijk brandstof voor de vlucht mee te nemen. Als bij
een vliegtuig de brandstoftanks helemaal vol zijn, gebruikt het
vliegtuig veel meer brandstof dan wanneer de tanks halfvol zijn. Het
vliegtuig is dan immers veel zwaarder. Een vliegtuig neemt dan ook
altijd precies de hoeveelheid brandstof mee die
voldoende is voor de lengte van de vlucht.
In de figuur hiernaast is voor een bepaald type vliegtuig het brandstofverbruik
per skm uitgezet tegen de vluchtlengte in km.Bij een vlucht van 9000 km zou
na elke 3000 km een tussenlanding gemaakt kunnen worden. |
 |
| |
Als de
vliegmaatschappij daartoe besluit, hoeft het vliegtuig bij elk
vertrek maar voor 3000 km aan brandstof mee te nemen en niet in
één keer voor 9000 km. Bereken hoeveel procent het
vliegtuig op deze manier aan brandstof per skm kan besparen. |
| |
|
|
|
|
| 6. |
Examenopgave HAVO Wiskunde A, 2017-II |
| |
|
|
|
|
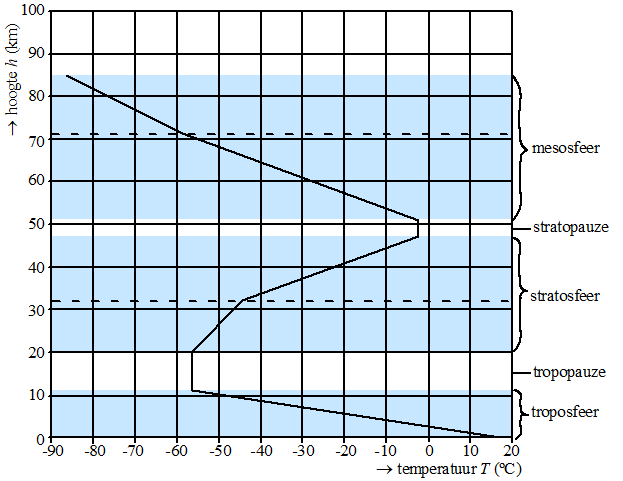
| |
De atmosfeer, ook wel dampkring
genoemd, is het gasvormige omhulsel van de aarde en is opgebouwd uit
verschillende lagen. De onderste drie lagen zijn de troposfeer, de
stratosfeer en de mesosfeer. De overgangszone tussen de onderste
twee lagen wordt de tropopauze genoemd, de overgangszone daarboven
de stratopauze. Zie de figuur.
De hoogtes waarop de verschillende lagen en overgangszones zich
bevinden, zijn niet overal op aarde gelijk en kunnen door de tijd
heen variëren. Om zaken toch goed te kunnen vergelijken heeft men
een model voor de onderste drie lagen en overgangszones vastgesteld:
de standaardatmosfeer. De temperatuur op een bepaalde hoogte is in
de figuur af te lezen. Daarin zie je het verband tussen de
temperatuur T in °C en de hoogte h in km. Zo kun je
aflezen dat op een hoogte van 10 km de temperatuur –50 °C is. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
In elk van de drie sferen is er een
laagste en hoogste temperatuur.
Bepaal in welke van de drie sferen het verschil
tussen de hoogste en laagste temperatuur het kleinst is. Licht je
antwoord toe. |
| |
|
|
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|