|
|||||||||
| 1. |
In een stad is het gewoonlijk warmer dan
op het platteland. Dit effect heet het “Island-Effect” en is door de
Wageningse onderzoeker
Gert-Jan Steeneveld
onderzocht. Hij heeft aangetoond dat er een lineair verband is tussen
de hoeveelheid groenbedekking (G, in procenten) van een stad en het
temperatuursverschil (T, in
°C)
tussen die stad en het platteland. Hij ontdekte de formule T = 2,7 – 0,058G Het gemiddelde verschil tussen stad en platteland in Nederland was 2,4°C. |
||||||||
| a. | Hoe groot is de groenbedekking in Nederland van een gemiddelde stad? | ||||||||
|
|||||||||
| b. | In een stad met oppervlakte 38 km2 is de hoeveelheid groenbedekking 6%. Bereken hoeveel km2 groen men bij moet planten om het temperatuursverschil met het platteland één graad lager te maken. | ||||||||
|
|||||||||
| Je kunt deze formule makkelijk gebruiken om bij een gegeven temperatuursverschil het groenpercentage van een stad te bepalen. Daarvoor is het handiger als je de formule schrijft als G = ….. | |||||||||
| c. | Druk G uit in T. | ||||||||
| Een collega onderzoeker uit Duitsland vond de formule T = 3,0 – 0,084G | |||||||||
| d. | Voor welke groenbedekking geven beide formules het zelfde temperatuursverschil? | ||||||||
|
|||||||||
| 2. |
In de volgende tabel vind je een aantal wereldrecords op de 800 meter atletiek voor mannen. |
||||||||
|
|||||||||
| In deze opgave nemen
we de tijd (t) in jaren met t = 0 in 1900 Verder rekenen we de tijd van een record (R) in seconden. Een record van 1:51,9 betekent dus 111,9 seconden Het blijkt dat er ongeveer een lineair verband bestaat tussen record R en tijdstip t. |
|||||||||
| a. | Stel met de gegevens van 1912 en 2010 zo’n lineaire formule op. | ||||||||
|
|||||||||
| b. |
Ook in
1951 is er een record gelopen, maar dat staat niet in deze tabel. Bereken door lineair interpoleren wat dit record ongeveer zal zijn geweest, |
||||||||
|
|||||||||
| Voor het vervolg van deze opgave nemen we de formule R = -0,125t + 113,4 | |||||||||
| c. | Bereken met deze formule algebraïsch wanneer het record voor het eerst onder de 95 seconden zal komen | ||||||||
|
|||||||||
| Het record van de
dames op deze afstand ligt wat lager. Daarvoor geldt de formule R = -0,212t + 163,9 |
|||||||||
| d. | Hoe kun je aan deze formules zien dat het damesrecord sneller verbetert dan het herenrecord? | ||||||||
| Als deze formules in de toekomst blijven gelden, dan zou er in theorie een jaar komen waarop de records voor de dames en heren gelijk zouden zijn | |||||||||
| e. | Bereken algebraïsch wanneer dat in theorie zal gebeuren | ||||||||
|
|||||||||
| 3. | In het Brabants
Dagblad van 28 mei 1997 beschrijft de bioloog Midas Dekkers hoe je een
krekel als thermometer kunt gebruiken. Het blijkt namelijk dat een
krekel meer sjirpen per minuut maakt als het warmer wordt! Dekkers heeft de volgende formule ontwikkeld: T = 0,2 · S + 10 Daarin is T de temperatuur en S het aantal sjirpen per minuut. |
||||||||
| a. | Johan zit op een zomeravond in zijn tuin en telt 40 sjirpen per minuut. Hoe warm is het? | ||||||||
|
|||||||||
| b. | Een week later telt hij weer het aantal sjirpen, en berekent dat het 15°C is. Hoeveel sjirpen telde hij per minuut als zijn berekening klopt? | ||||||||
|
|||||||||
|
Een andere
bioloog gebruikt de volgende regel om de temperatuur te berekenen: ”Trek 25 af van het aantal sjirpen, deel daarna door 5 en tel er tenslotte 10 bij op” |
|||||||||
| c. | Maak een formule die bij deze regel past en onderzoek daarna of deze regel dezelfde antwoorden geeft als de formule van Dekkers. | ||||||||
| 4. | Mevrouw Hak is voorlichter van een fabrikant van diepvriesgroenten. Met de formule H = 12 – 1,2T berekent ze de houdbaarheid van de groenten. Hierin is H de houdbaarheid in dagen, en T de bewaartemperatuur in graden Celsius. | ||||||||
| a. | Hoe kun je in één keer en zonder berekeningen te maken aan deze formule zien dat bij een lagere temperatuur een hogere houdbaarheid hoort? | ||||||||
| b. | Bij welke temperatuur zal de houdbaarheid precies één week zijn? | ||||||||
|
|||||||||
| 5. |
Een
werknemer wil in verband met zijn nieuwe baan gaan verhuizen van
Groningen naar Maastricht. Daarvoor zoekt hij een verhuisbedrijf. Hij
heeft berekend dat alles wel in één verhuiswagen kan, en leest de
offertes van twee verhuisbedrijven. Het betreft de bedrijven Budget
Verhuisservice, Mast BV. Elk bedrijf vraagt voor het gebruik van een verhuiswagen een vast bedrag per dag. Verder komt daar nog bovenop een bedrag per kilometer. Budget Verhuisservice vraagt voor de wagen €400,- en verder per km nog €2,50. Mast BV vraagt voor de wagen €550,- en verder per km nog €1,60. |
||||||||
| a. | Stel formules op voor de totale vervoerkosten K als functie van de afstand a | ||||||||
| b. | Bereken algebraïsch bij welke afstanden Mast BV het goedkoopst is. | ||||||||
|
|||||||||
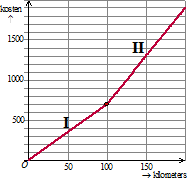
| Een derde bedrijf, Nieuwenhuis Verhuizingen, vraagt alleen een kilometervergoeding: de eerste 100 km kost een verhuizing €7,- per km en elke km daarboven kost het meer per km. Hiernaast staat de grafiek voor de kosten van Nieuwenhuis. Die bestaat uit twee delen |
|
||||||||
|
|
|||||||||
| c. | Welk van beide delen beschrijft een evenredig verband? Leg uit. | ||||||||
| d. | Geef een formule voor het tweede deel. | ||||||||
| 6. | Examenvraagstuk HAVO Wiskunde A, 2010. | ||||||||
| Een gasleverancier heeft onderzocht hoe de hoeveelheid
te leveren gas afhangt van de buitentemperatuur. Uit dat onderzoek blijkt dat er altijd een vaste hoeveelheid gas gebruikt wordt voor koken, douchen en dergelijke. Deze constante hoeveelheid is 5,5% van de maximale capaciteit van het netwerk (het constante deel). De hoeveelheid gas die wordt gebruikt voor het verwarmen van huizen en andere gebouwen, is afhankelijk van de buitentemperatuur (het temperatuurafhankelijke deel). In deze opgave bekijken we het percentage van de maximale capaciteit van het netwerk dat gebruikt wordt voor het gastransport. Dit percentage P wordt gegeven door de volgende formule. Hierin is T de buitentemperatuur in °C. |
|||||||||
|
|
|||||||||
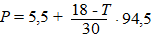| a. | De formule is niet meer bruikbaar boven een bepaalde buitentemperatuur, omdat het percentage altijd minstens 5,5 is. Bereken deze buitentemperatuur. | ||||||||
|
|||||||||
| b. | De formule is ook niet bruikbaar voor lagere temperaturen dan T = –12 °C. Toon dit met behulp van de formule aan. | ||||||||
| De formule voor P kun je herleiden tot de bekende vorm: P = a • T + b | |||||||||
| c. | Bereken a en b. | ||||||||
|
|||||||||
| 7. | Examenvraagstuk HAVO Wiskunde A, 2010. | ||||||||
| Duinwaterbedrijf Zuid-Holland is
een bedrijf dat de levering van drinkwater verzorgt. Het bedrijf bepaalt
ieder jaar opnieuw de tarieven van het drinkwater dat zij leveren. In 2007 werd het tarief per m3 drinkwater verlaagd met €0,14 ten opzichte van het tarief van 2006. Het nieuwe tarief in 2007 werd €1,10. Tegelijkertijd werd het vastrecht verhoogd van €47,52 in het jaar 2006 tot €52,80 in het jaar 2007. |
|||||||||
| a. | Bereken met deze gegevens bij welk drinkwaterverbruik je in 2007 goedkoper uit bent dan in 2006. | ||||||||
|
|||||||||
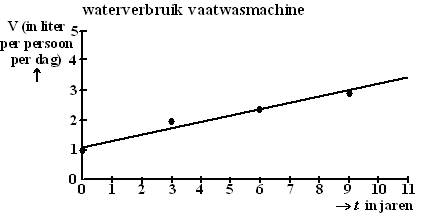
| Lang niet al het
drinkwater wordt gebruikt om te drinken.
Een gedeelte van het drinkwater wordt gebruikt voor de vaatwasmachine. Gegevens daarvan staan in de figuur hiernaast, waarbij geldt dat 1995 overeenkomt met t = 0. In deze grafiek kun je bijvoorbeeld aflezen dat er in 2001 (t = 6) gemiddeld over alle Nederlanders ongeveer 2,4 liter water per persoon per dag wordt gebruikt voor vaatwasmachines. Het lijkt erop dat V, het waterverbruik van de vaatwasmachine in liter per persoon per dag, bij benadering lineair toeneemt. |
 |
||||||||
| Daarom is een lijn
getekend die zo goed mogelijk bij de gegevens past. De formule van de lijn is V = a • t + b , waarbij t de tijd is in jaren na 1995. |
|||||||||
| b. | Bereken a en b en rond af op één decimaal. | ||||||||
|
|||||||||
| Voor de berekening
van het waterverbruik deelt men het totale waterverbruik voor de vaatwasmachine
in een bepaald jaar door het aantal dagen van het betreffende jaar en
door het totaal aantal Nederlanders in dat jaar. Als in de berekening alleen rekening gehouden wordt met personen die werkelijk de beschikking hebben over een vaatwasmachine, valt het verbruik per persoon per dag hoger uit. Dit verbruik wordt het gecorrigeerde waterverbruik van de vaatwasmachine (in liter per persoon per dag) genoemd. In 2004 beschikte 58% van de 16 miljoen Nederlanders over een vaatwasmachine. |
|||||||||
| c. | Bereken het gecorrigeerde waterverbruik voor de vaatwasmachine (in liter per persoon per dag) in dat jaar. | ||||||||
|
|||||||||
| 8. |
|
||||||||
| 9. | Examenvraagstuk HAVO Wiskunde A, 2011. | ||||||||
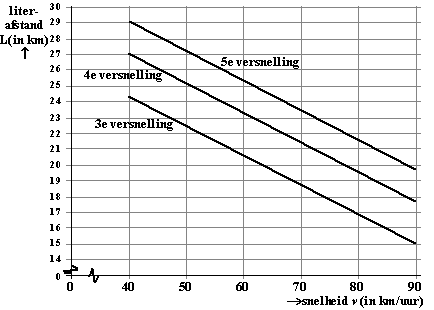
| De Literafstand (L) is het
aantal km dat je met een auto met 1 liter benzine kunt afleggen. Deze
literafstand hangt af van de snelheid waarmee er gereden wordt. De
literafstand hangt ook af van in welke versnelling er gereden wordt. De resultaten van een onderzoek daarnaar zijn in de figuur hiernaast grafisch weergegeven. |
 |
||||||||
| In de figuur kun je voor de derde, vierde en de vijfde versnelling bij iedere snelheid de literafstand aflezen. De figuur bestaat uit drie evenwijdige rechte lijnen. | |||||||||
| Je rijdt 70 km per uur in de vierde versnelling. | |||||||||
| a. | Bepaal met behulp van de figuur met welke snelheid je in de derde versnelling kunt rijden bij dezelfde literafstand. Licht je werkwijze toe. | ||||||||
|
|||||||||
| Voor de vierde en de vijfde
versnelling worden deze lineaire verbanden beschreven door de formules: Lvierde versnelling = −0,1838 • v + 34,33 Lvijfde versnelling = −0,1838 • v + 36,38 Hierin is L de literafstand in km en v de snelheid in km per uur. De formule voor de literafstand in de derde versnelling Lderde versnelling ontbreekt in het bovenstaande. |
|||||||||
| b. | Stel op basis van bovenstaande gegevens deze formule op. | ||||||||
| c. | Als je wilt weten met welke
snelheid je mag rijden in de vijfde versnelling om een bepaalde
literafstand te halen, is het handig het gegeven verband tussen de
literafstand en de snelheid te schrijven in de vorm: v =
a • Lvijfde versnelling + b Leid uit het gegeven verband tussen Lvijfde versnelling en v een formule van bovenstaande vorm af. Rond a en b af op één decimaal. |
||||||||
|
|||||||||
| 10. | Examenvraagstuk
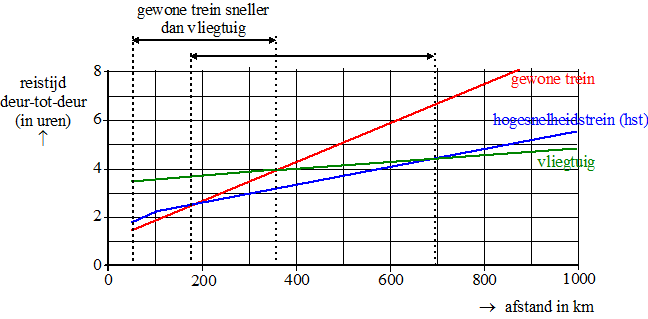
VWO Wiskunde C, 2011. In 2010 stond in NRC Handelsblad een artikel waarin de prestaties van vliegtuig, hogesnelheidstrein (hst) en gewone trein met elkaar vergeleken werden. Bij het artikel stond onderstaande figuur. In deze figuur staat horizontaal de reisafstand in kilometers en verticaal de totale reistijd van-deur-tot-deur in uren. De reistijd van-deur-tot-deur is de totale tijd die nodig is voor de trein- of vliegreis zelf en voor de verplaatsingen van en naar het station of vliegveld. |
||||||||
|
|
|||||||||
| Uit de figuur blijkt dat men voor reizen met een afstand van meer dan 100 km bij elk vervoermiddel uitgaat van een constante snelheid | |||||||||
| a. | Bereken deze snelheid voor de hogesnelheidstrein in km/u. | ||||||||
|
|||||||||
| Voor een reis met de auto is er geen reistijd van en naar een station of vliegveld. Neem daarom aan dat we bij autoreizen ook bij afstanden beneden de 50 km uit mogen gaan van een constante snelheid. | |||||||||
| b. | Teken in de figuur de grafiek van het reizen met de auto met een snelheid van 100 km/u en bepaal daarmee tot welke afstand de auto sneller is dan het vliegtuig. | ||||||||
| Naar aanleiding van de figuur heeft men de volgende formules opgesteld. Hierbij is a de afstand in km en r de reistijd in uren: | |||||||||
| Vliegtuig: r = 0,00137a + 3,43 | |||||||||
| Gewone trein: r = 0,00793a + 1,10 | |||||||||
| c. | Onderzoek met behulp van deze formules vanaf welke afstand de reistijd met het vliegtuig kleiner is dan de reistijd met de gewone trein. | ||||||||
|
|||||||||
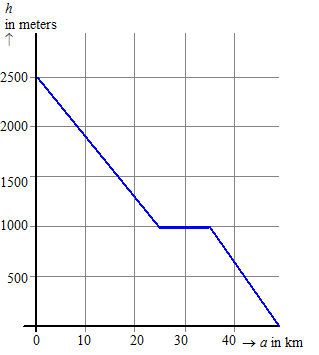
| 11. | Hiernaast zie de de grafiek van
de hoogte h (in meters) van een landend vliegtuig. Op de x-as
staat de horizontale afstand tot het punt vanaf waar de landing is
begonnen. Er zijn drie fasen bij de landing. In de eerste 25 km daalt het vliegtuig 1500 meter, en de tweede fase blijft de hoogte constant. In deze fase wordt afgeremd, wat met veel geluidsoverlast gepaard gaat. In de laatste fase daalt het vliegtuig tot de landingsbaan. |
|
|||||||
| a. | Stel formules op bij fase 1 en fase 3. | ||||||||
| Om geluidsoverlast te beperken
wordt tegenwoordig een glijvluchtlanding gepropageerd. Zo'n
glijvluchtlanding begint op 35 km van de landingsbaan (horizontaal). Tot
daar vliegt het vliegtuig op 2500 m hoogte. Vanaf dat punt daalt het vliegtuig in één rechte lijn naar de landingsbaan. |
|||||||||
| b. | Stel een formule op voor een glijvluchtlanding. Rond de constanten in je formule af op één decimaal. | ||||||||
| 12. |
|
||||||||
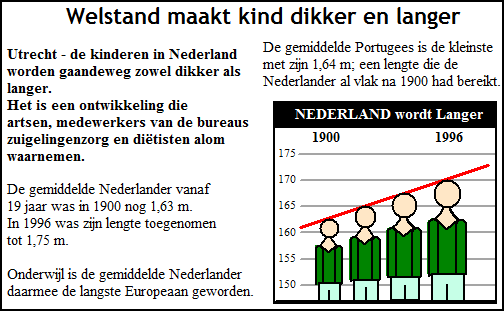
| In de grafiek zie je hoe de
gemiddelde lengte van de Nederlander sinds 1900 is toegenomen. Deze
groei blijkt lineair te zijn. Voor de gemiddelde lengte geldt:
L(t) = 163 + 0,125t Daarbij is t = 0 in 1900 en t in jaren en L in cm. |
|||||||||
| a. | Leg duidelijk uit hoe die formule is af te leiden uit het krantenartikel. | ||||||||
| b. | De gemiddelde Griek heeft een lengte van 168 cm. In welk jaar had de gemiddelde Nederlander deze lengte bereikt? | ||||||||
|
|||||||||
| De Nederlander is nu het langst,
maar de Duitsers zijn in aantocht! Voor hun gemiddelde lente geldt: D(t) = 161,5 + 0,138t |
|||||||||
| c. | Als deze groei zo doorgaat, in welk jaar haalt Duitsland Nederland dan in? | ||||||||
|
|||||||||
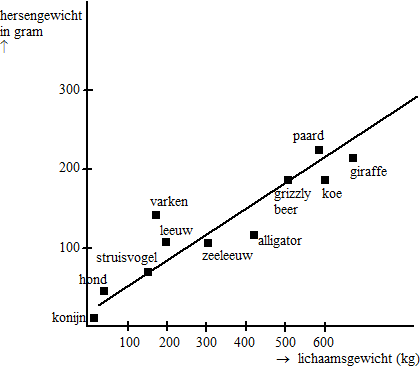
| 13. | In de figuur hiernaast zie je het
hersengewicht (H, in gram) van een aantal diersoorten als functie van
hun lichaamsgewicht (L, in kg). Er is een rechte lijn getekend die zo goed mogelijk bij de gegevens past. De meetwaarden van de struisvogel (150 kg, 70 gram) en de grizzlybeer (520 kg, 180 gram) liggen precies op die lijn. |
 |
|||||||
| a. | Geef een vergelijking van deze lijn. | ||||||||
| Natuurlijk zijn er door deze
punten meer lijnen te trekken. Twee onderzoekers komen met twee
verschillende modellen: I: H = 0,32L + 24,2 II: H = 0,28L + 26,5 |
|||||||||
| b. | Bereken hoeveel procent de werkelijke herseninhoud van een varken zwaarder is dan die volgens model II | ||||||||
| c. | Bereken algebraïsch voor welk lichaamsgewicht beide formules dezelfde herseninhoud voorspellen. | ||||||||
|
|||||||||
| 14. | Recente studies wijzen uit dat de
gemiddelde oppervlaktetemperatuur van de aarde langzaamaan aan het
toenemen is. Een aantal Amerikaanse wetenschappers heeft een lineair
model opgesteld, namelijk T = 0,016t + 8,48 Daarin is T de gemiddelde oppervlaktetemperatuur (in ºC) en t de tijd in jaren met t = 0 in 1900. |
||||||||
| a. | Wat stelt het getal 0,016 in praktijk voor? | ||||||||
| b. | Bereken algebraïsch wanneer volgens dit model de temperatuur gelijk zal zijn aan 12ºC | ||||||||
|
|||||||||
| Een groep Russische wetenschappers gebruikt het model T = 0,018t + 7,90 | |||||||||
| c. | Bereken algebraïsch voor welk jaar beide modellen dezelfde temperatuur voorspellen. | ||||||||
|
|||||||||
| 15. | De aanbevolen hoeveelheid van een
geneesmiddel is voor een kind altijd minder dan voor een volwassene. Men hanteert de volgende vuistregel: K = 0,053 • V • (L + 2) Daarbij is K de hoeveelheid voor een kind in mg, V de hoeveelheid voor een volwassene in mg, en L de leeftijd in jaren. |
||||||||
| a. | Stel dat de hoeveelheid voor een
volwassene gelijk is aan V = 200 mg. Schets dan de grafiek van K en leg duidelijk uit wat de helling voorstelt. |
||||||||
| b. | Op welke leeftijd ben je volgens deze formule volwassen? | ||||||||
|
|||||||||
| c. | Op welke leeftijd krijgt een kind de helft van de dosis van een volwassene? | ||||||||
|
|||||||||
| 16. | Examenvraagstuk
VWO Wiskunde A, 2018-I. |
||||||||
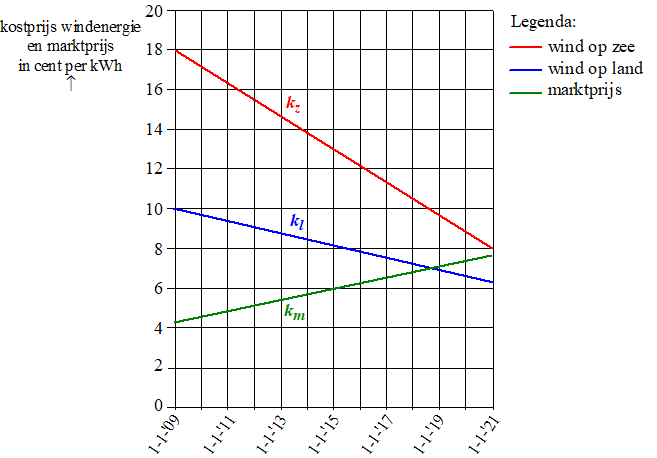
| In een krant stond eind 2013 bij een artikel over de toekomst van windenergie de onderstaande figuur. In de figuur wordt de kostprijs voor het produceren van windenergie vergeleken met de kosten voor het produceren van energie in een traditionele kolencentrale (de marktprijs) | |||||||||
|
|
|||||||||
| De grafieken zijn
gebaseerd op een model van de werkelijkheid. Met behulp van dit model is
het mogelijk om op ieder willekeurig tijdstip de kostprijs van energie
uit te rekenen.
De formule voor de marktprijs
km
luidt:
km
=
0,28 •
t +
4,3 |
|||||||||
|
Voor beide formules geldt: k is de prijs in cent per kWh (kilowattuur) en t is de tijd in jaren met t = 0 op 1 januari 2009. We nemen in deze opgave aan dat de prijzen zich ook na
2020 volgens deze lineaire verbanden blijven ontwikkelen. |
|||||||||
| a. | Stel met behulp van de figuur een formule op voor de kostprijs kz van windenergie van windmolens op zee en bereken daarmee in welk jaar de windenergie van land en die van zee evenveel kosten. | ||||||||
|
|||||||||
| Rond 2011 was de kostprijs van windenergie van windmolens op land nog tweemaal zo hoog als de marktprijs. | |||||||||
| b. | Bereken in welk jaar de marktprijs tweemaal zo hoog zal zijn als de kostprijs van windenergie van windmolens op land. | ||||||||
|
|||||||||
| 17. |
|
||||||||
|
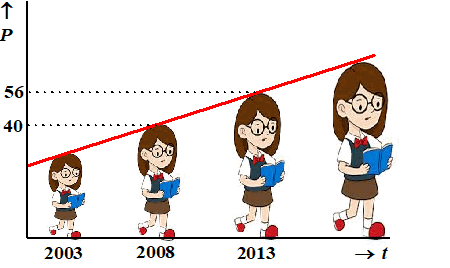
Het volgende berichtje stond in het NRC in 2013 Amsterdam - De meisjes in Nederland gaan gaandeweg meer en meer een bètaprofiel kiezen. Het is een ontwikkeling die alom op middelbare scholen wordt waargenomen. Niet alleen kiezen de meisjes steeds vaker een bétaprofiel, ze zijn daarin ook steeds succesvoller. Het zal niet lang meer duren totdat ook bij universitaire bétastudies de meisjes de overhand zullen krijgen.
In 2008 koos nog slechts 40% van de meisjes een bètaprofiel, maar in
2013 was dat aantal gegroeid tot 56%. |
|||||||||
| a. | Neem aan dat de groei in het percentage meisjes lineair was, en stel een formule op voor het percentage van de meisjes (P) en de tijd t in jaren. | ||||||||
|
Vanaf 2013 bleef het aantal meisjes groeien, alhoewel het iets minder
snel ging. |
|||||||||
| b. | Bereken algebraïsch wanneer het percentage jongens minder dan 50% zal zijn. | ||||||||
| c. |
Als deze groei zo doorgaat, in welk jaar zal het percentage van de meisjes dan voor het eerst meer dan dubbel zo groot zijn als het percentage van de jongens? |
||||||||
| 18. | Examenvraagstuk VWO Wiskunde
A, 2022-III In Nederland drukken we temperaturen meestal uit in graden Celsius (°C), maar er bestaan veel meer temperatuurschalen. In deze opgave bekijken we een aantal van deze temperatuurschalen. In de Verenigde Staten wordt de temperatuur uitgedrukt in graden Fahrenheit (°F). De Fahrenheitschaal is in 1724 ontwikkeld door de Duitser Gabriel Fahrenheit. Hij gebruikte bij het bedenken van deze schaal de volgende drie referentiepunten: |
||||||||
| 1. | Hij maakte een
mengsel van ijs, water en een bepaald soort zout. Dat was in die tijd de
manier om een zo laag mogelijke temperatuur te verkrijgen. Die temperatuur noemde hij 0 °F. |
||||||||
| 2. | Het vriespunt van water. Dat noemde hij 32 °F. | ||||||||
| 3. | De lichaamstemperatuur van een gezond mens. Die noemde hij 96 °F | ||||||||
| In graden Celsius is de lichaamstemperatuur van een gezond mens gelijk aan 37 °C en is het vriespunt van water 0 °C. Zowel de Celsiusschaal als de Fahrenheitschaal is lineair. En ook het verband tussen de temperatuur in graden Celsius en die in graden Fahrenheit is lineair. | |||||||||
| a. | Bereken met behulp van de bovenstaande referentiepunten de temperatuur in °C van het ijsmengsel dat Fahrenheit gebruikte. | ||||||||
|
|||||||||
| De metingen van
Fahrenheit waren vrij onnauwkeurig en daarmee was zijn temperatuurschaal
dat ook. Inmiddels is de Fahrenheitschaal nauwkeuriger vastgesteld en
geldt tussen graden Celsius (C) en graden Fahrenheit (F) het volgende
verband: C = 5/9 • (F - 32). |
|||||||||
| b. | Bereken bij welke temperatuur beide temperatuurschalen dezelfde temperatuur aangeven. | ||||||||
|
|||||||||
| In de wetenschap
werkt men meestal met de Kelvinschaal. Deze schaal is afgeleid van de
Celsiusschaal, maar heeft een ander nulpunt, namelijk het zogenoemde
absolute nulpunt. Dat is de laagst mogelijke temperatuur. In graden Celsius is dat −273,15 °C. Er geldt: K = C + 273,15 met K in Kelvin. Door de twee bovenstaande formules te gebruiken, kun je een formule opstellen die de temperatuur in Kelvin uitdrukt in graden Fahrenheit. Deze formule heeft de vorm K = aF + b |
|||||||||
| c. | Bereken de waarden van a en b. Geef je antwoorden in twee decimalen. | ||||||||
|
|||||||||
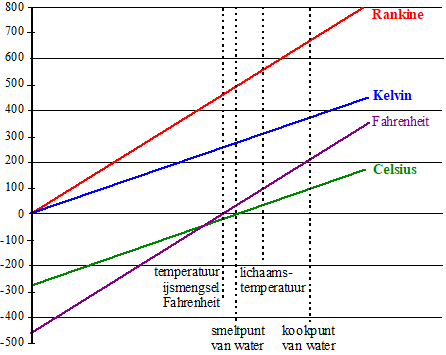
| In de figuur zijn de grafieken getekend van verschillende temperatuurschalen: Celsius, Fahrenheit en Kelvin. Beide assen hebben een lineaire schaalverdeling. Op de horizontale as is echter geen schaalverdeling weergegeven: daar staan enkele natuurkundige verschijnselen die bij de betreffende temperaturen plaatsvinden. In de figuur is ook de grafiek getekend van de schaal van Rankine. Deze schaal is in de negentiende eeuw afgeleid van die van Fahrenheit, maar heeft, net als de Kelvinschaal, het absolute nulpunt als nulpunt. De grafieken die horen bij Fahrenheit en Rankine zijn evenwijdig. | |||||||||
|
|
|||||||||
| Met behulp van deze
grafieken en/of de voorgaande formules is het mogelijk om een verband op
te stellen tussen de temperatuur in °C en die in graden Rankine (°Ra).
Dat verband heeft de vorm: C = pR + q met C de temperatuur in °C en R de temperatuur in °Ra. |
|||||||||
| d. | Stel deze formule op. Licht je antwoord toe en geef de waarden van p en q in twee decimalen. | ||||||||
| 19. | Examenvraagstuk HAVO Wiskunde
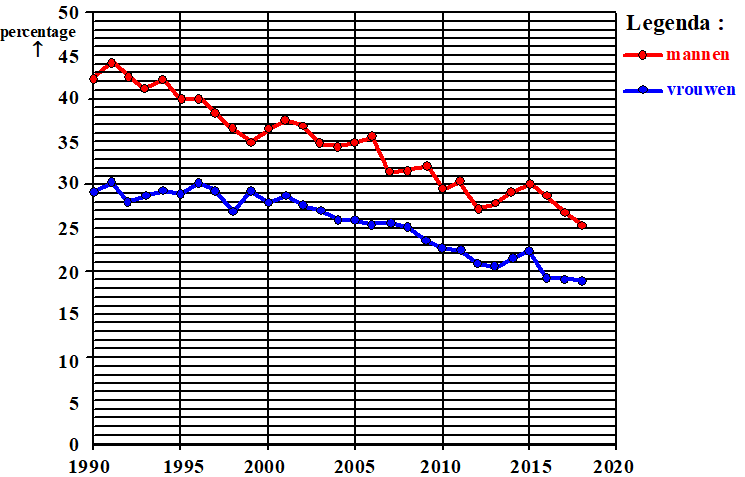
A, 2023-II De onderstaande iguur komt uit het rapport Volksgezondheid Toekomst Verkenning 2018 van het RIVM (Rijksinstituut voor Volksgezondheid en Milieu). In deze figuur zijn voor Nederland het percentage van de mannen dat rookt en het percentage van de vrouwen dat rookt op 1 juli voor de jaren 1990 tot en met 2018 weergegeven. |
||||||||
|
|
|||||||||
| Voor de periode vanaf 2018 heeft het RIVM een formule opgesteld om de ontwikkeling van het percentage van de mannen dat rookt te voorspellen. Men gaat uit van een lineaire afname volgens de volgende formule: | |||||||||
|
Pm = -0,61t + 25,93 (formule 1) |
|||||||||
| Hierin is Pm
het percentage van de mannen dat rookt en t het aantal jaren
vanaf 1 juli 2018. Het RIVM beweert dat volgens formule 1 het percentage van de mannen dat rookt voor de start van het jaar 2040 gehalveerd is ten opzichte van 1 juli 2018. |
|||||||||
| a. | Onderzoek of deze bewering juist is. | ||||||||
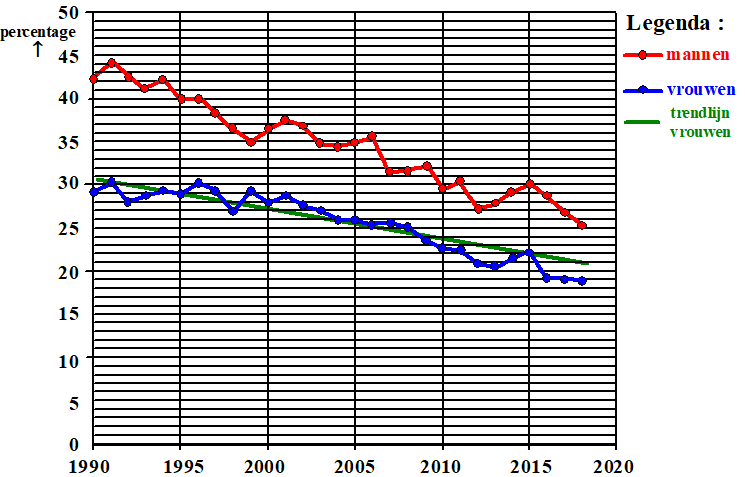
| De onderstaande figuur is ontstaan door in de vorige figuur de trendlijn te tekenen voor het percentage van de vrouwen dat rookt. | |||||||||
|
|
|||||||||
| De percentages van
de vrouwen die roken op 1 juli in 1995 en 2004 liggen precies op de
trendlijn. Met deze gegevens kan een formule voor de trendlijn worden opgesteld: |
|||||||||
|
Pv = -0,33t + 30,67 (formule 2) |
|||||||||
| Hierin is Pv
het percentage van de vrouwen dat rookt en t het aantal jaren
vanaf 1 juli 1990. De percentages van de vrouwen die roken in 1995 en 2004 zijn gehele getallen. |
|||||||||
| b. | Bereken met deze percentages de getallen in formule 2 in drie decimalen. | ||||||||
| Het percentage van de mannen dat rookt, kan vanaf 1 juli 2018 worden berekend met formule 1. Het percentage van de vrouwen dat rookt, kan vanaf 1 juli 1990 worden berekend met formule 2. | |||||||||
| c. | Onderzoek in welk jaar het percentage van de mannen dat rookt en het percentage van de vrouwen dat rookt gelijk zullen zijn. | ||||||||
|
|||||||||
 |
|||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||
