Extremen.

© h.hofstede (h.hofstede@hogeland.nl)
Extremen van de grafiek zijn toppen en dalen van die grafiek. De maxima en minima.
't Is een verzamelnaam voor beiden.
Extremen van een grafiek zijn erg interessant....

Waarom?

Nou, droom maar even mee, stel je voor.....

• ...dat je een formule voor de winst van je bedrijfje hebt als functie van het aantal producten dat je gaat produceren. Dan is het toch wel érg interessant bij welke productiegrootte die winst maximaal is.
• ...dat je weet hoe de oppervlakte van een literblik afhangt van de hoogte. Dan wil je graag weten bij welke hoogte die oppervlakte minimaal is, want dan heb je het minste materiaal nodig om je blik te maken.
• ...dat je  een formule hebt ontdekt die zegt hoe goed gistcellen werken bij een bepaalde temperatuur. Dan wil je natuurlijk meteen weten bij welke temperatuur hun werking maximaal is. Toch?
Geef maar toe: extremen zijn gewoon interessant!
Wiskundig is het gelukkig erg makkelijk zulke maxima en minima van een grafiek op te sporen. Je ziet het vast meteen in de volgende grafiek. Daar is bij elk maximum en elk minimum de raaklijn getekend.
De quizvraag van vandaag is natuurlijk:  "Wat valt je op????????"
Nou ik kan me haast niet voorstellen dat iemand het niet ziet:  Die raaklijnen zijn allemaal horizontaal.
Maar dat betekent dat de helling van die lijnen nul  is.
Maar dat betekent dat de heling van de grafiek zélf daar ook nul is.

AHA.......  dat is f '!!!

Dat geeft ons een manier om maxima en minima  (extremen) op te sporen:

Bij een maximum of minimum van  f  geldt  f ' = 0
Maar ehmm.... Hoe weet je nou of 't een maximum of een minimum is ?

De simpelste manier om daar achter te komen is om de grafiek te plotten en gewoon te kijken of er een top of een dal zit bij de x die je hebt berekend. 
De tweede (en iets nettere) manier is om een zogenaamd tekenbeeld van de afgeleide functie te maken.
Dat komt later.

   
  OPGAVEN
1. Bereken algebraïsch welke extremen de volgende functies hebben. Geef elke keer ook aan of het om een maximum of een  minimum gaat.
         
a. f(x) = 2x2 + 8x + 7 d. f(x) = 1/x + 3x2
b. y = x3 - 9x2 + 24x - 24 e. f(x) = 8/x² + 2x - 3
c. y = √x - 2x f. y =  x√x - 0,75x2
2. Vroeger heb je ooit geleerd dat de top van de parabool y = ax2 + bx + c  ligt bij  x = - b/2a
Toon dat aan met behulp van de afgeleide.
3. Een ijsverkoper merkt dat het aantal ijsjes dat hij op een dag verkoopt toeneemt als hij de prijs ervan verlaagt (ja dûh). Op dit moment verkoopt hij zijn ijsjes voor €1,50 per stuk en hij verkoopt 250 ijsjes per dag, dus dat levert hem een omzet van  250 • 1,50 = €375,- per dag
Hij experimenteert een beetje en komt tot de conclusie dat voor elke 10 cent dat hij van de prijs afhaalt, hij 20 ijsjes extra verkoopt.
Stel dat hij uiteindelijk besluit om d dubbeltjes van de prijs af te halen.
Dan is zijn totale omzet (het bedrag dat hij per dag binnenkrijgt) gelijk aan O = 375 + 5d  - 2d2
     
a. Toon aan dat die formule klopt.
     
b. Bij welke prijs is de omzet van deze verkoper maximaal?

€1,375
   
4. Ik kocht op 1 januari 2000 een pakket aandelen. In de dagen die volgden hield ik goed de waarde van mijn pakket in de gaten. Het ging geweldig! Er bleek te gelden:
W(t) = 0,7t3 - 35t2 + 500t + 1000
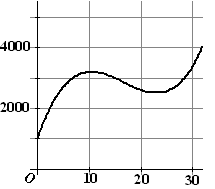
Daarbij is t de tijd in maanden met t = 0 op 1 januari 2000, en W de waarde van mijn aandelenpakket in euro.
De grafiek van deze functie staat hiernaast gegeven.
Beantwoord de volgende vragen algebraïsch.

a. Ik heb een poosje slecht geslapen toen de waarde van mijn aandelen daalde. Hoe lang duurde dat poosje?
 

≈12,6 maand
b. Op welk tijdstip nam de waarde van mijn aandelen toe met  een snelheid van €100,- per maand?

7,3  en 26,0
   
5. Gegeven zijn de functies:  fa(x) = 2ax - 8√x
     
a. Geef de vergelijking van de raaklijn aan de grafiek van f1 in het punt waarvoor x = 1.
   

y = -2x - 4
b. Er is een functie fa die een minimum heeft bij x = 16. Bereken de y-coördinaat van dat minimum.
     

y = -16
       
6. Gegeven is de functie  f(x) = x - a√(x + 1)
Voor welke waarde van a heeft deze functie een extreme waarde -3?
     
a = 2√2
7. Een luie wiskundige moet de wortel trekken uit een groot aantal getallen tussen 0 en 1. Hij heeft geen rekenmachine en besluit om gewoon te doen alsof de wortel van een getal gelijk is aan het getal zelf.
Zo zegt hij bijvoorbeeld gewoon √0,8 = 0,8. Het scheelt niet eens zoveel.
De fout die hij maakt is dus gelijk aan √0,8 - 0,8.
Wat is de maximale fout die hij op deze manier kan maken?  
 

≈0,1338
   
8. De verkoopcijfers van een bepaald product zijn lange tijd constant, maar de fabrikant wil graag meer gaan verkopen. Op tijdstip t = 5 lanceert men daarom een reclamecampagne. Het blijkt dat de verkoopcijfers direct vanaf dat tijdstip sterk stijgen. Echter het is een bekend verschijnsel in de reclamewereld dat dit effect maar van korte duur is: het publiek raakt gewend aan de reclames en het effect ervan neemt af. De verkoopcijfers naderen weer langzaam tot hun oude niveau.
Voor de toename van de verkoopcijfers (in procenten) blijkt te gelden:
T = 1680/t - 8400/t²  
Daarin is t de tijd in weken en T de toename van de verkoopcijfers. De formule geldt voor t > 5.
     
a. Toon met behulp van differentiëren aan dat de verkoopcijfers op t = 5 inderdaad stijgen.
     
  b. Hoeveel procent toename zal maximaal gehaald worden?
   

T = 84
     
9. Gegeven zijn de functies  fp(x) = x3 + 3x2 + px + p
     
  a. Bereken algebraïsch de coördinaten van de extremen van f0,57.
   

(2,92) (4, -88)
  b. Geef een vergelijking van de raaklijn aan de grafiek van f2 in het punt waar x = 1
   

y = 11x - 3
  c. Bewijs dat alle grafieken van fp door hetzelfde punt gaan.
     
  d. Vanaf bepaalde p heeft de grafiek van fp geen extremen meer.
Onderzoek met je GR welke p dat is, en probeer vervolgens met formules te verklaren waarom dat zo is.
   

p = 3
     
10. Teken  in één figuur een tweedegraads functie f en een eerstegraads functie g zodat de grafieken elkaar raken en zodat bovendien geldt dat g de afgeleide van f  is.
     
11. Een banketbakker begint elk jaar ruim vóór Sinterklaas al met de verkoop van chocoladeletters.
Voor het aantal letters dat hij per dag verkoopt geldt de formule  L(t) = 90t - 20t1,5
Hij begint met de verkoop op t = 0, en dat is op 18 november.
     
  a. Leg uit dat de man ook na 5 december nog een aantal dagen chocoladeletters zal verkopen.
Hoeveel dagen?
   

3 dagen
  b. Bereken het maximale aantal letters dat hij op een dag zal verkopen.
   

L = 270
  c. Op een gegeven moment merkt hij dat hij op een dag 24 letters minder verkoopt dan de dag ervoor.
Wanneer zal dat zijn geweest?  Geef een berekening met behulp van de afgeleide L' .
   

3 dec.
     
12. Er is een uitgebreid onderzoek geweest naar het gedrag van gamers. Daar is immers veel geld aan te verdienen. Men was vooral benieuwd naar hoeveel uur per week een gamer aan een spel besteedt.
Uit het onderzoek bleek dat bij een typische gamer in het begin die tijd groter en groter wordt (als de gamer langzaamaan "gegrepen" wordt door het spel), maar ook dat na een poosje de piek voorbij is, en de gamer verveeld of geïnteresseerd in een ander spel raakt.

Men ontwikkelde de formule  T(w) = -w3 + 4w2 + 12w

Daarin is T de tijd in uren per week die de gamer aan een spel besteedt, en w het aantal weken met w = 0 op het moment dat hij aan het spel begint.
     
  a. Bereken algebraïsch hoeveel uur per week een gamer maximaal aan een spel besteedt.
   

48,52.
  b. Een gamer is op dit moment twee spellen af en toe aan het spelen. Met het ene spel is hij 1 week geleden begonnen, met het andere spel 2 weken geleden.
Bereken hoeveel zijn gametijd tussen vandaag en morgen zal toenemen of afnemen.
   

4,69 uur.

© h.hofstede (h.hofstede@hogeland.nl)