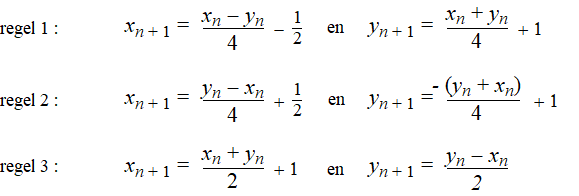© h.hofstede (h.hofstede@hogeland.nl)

De Draakkromme.
       
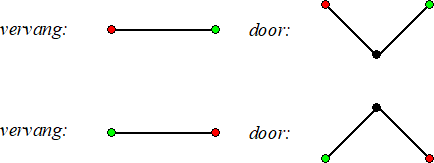
We kwamen de draakkromme al in een opgave van een  eerdere les tegen. Daar zagen we dit recept:
       
Startfiguur:        

     
Recept:  
    (de hoek is 90º)
Kleur daarna alle knooppunten om-en-om rood en groen,
te beginnen met rood.
       
En dat leidt uiteindelijk tot deze figuur:
       

       
Het is een mooie kromme met veel verrassende eigenschappen.

Vouwen maar!
Je kunt hem (haar?) bijvoorbeeld heel eenvoudig maken door en lange strook papier herhaaldelijk dubbel te vouwen. Als je dan na afloop het papier weer ontvouwt en alle hoeken op de vouwlijnen 90º maakt komt de drakenkromme tevoorschijn:
       

       
Dimensie.
Laten we de dimensie berekenen.
Er zijn 2 exemplaren nodig met elk lengte 1/√2 van het origineel (ze vormen een 1-1-√2 driehoek)
2 = (√2)D  geeft  D = 2.
De draakkromme heeft de dimensie van een vlakke figuur.
Dat betekent dat de draakkromme een vlakvullende kromme is!! Dat betekent dat je in theorie elk punt van het vlak kunt bereiken door maar lang genoeg door te gaan. De grens van de draakkromme blijft wel een fractal.
       
Opbouwen.
In plaats van lijnstukken steeds onder te verdelen kun je de draak ook opbouwen. Een volgende stap ontstaat daarbij door de hele vorige figuur over 90º om het uiteinde te draaien tegen de klok in.

 

     

BRON:  https://en.wikipedia.org/wiki/Dragon_curve
Het Chaos-spel.
       
In deze les staat beschreven hoe het zogenaamde "Chaos-spel" een fractal kan produceren.
De draakkromme ontstaat door steeds één van de volgende regels random te kiezen om  van punt (xn , yn)
naar punt  (xn + 1, yn + 1)  te gaan.
       

       
De draak in een kooi.
       
De hele draakkromme past  in een rechthoek.
Hoe groot is die rechthoek?
       
Ingesloten oppervlakte.
       
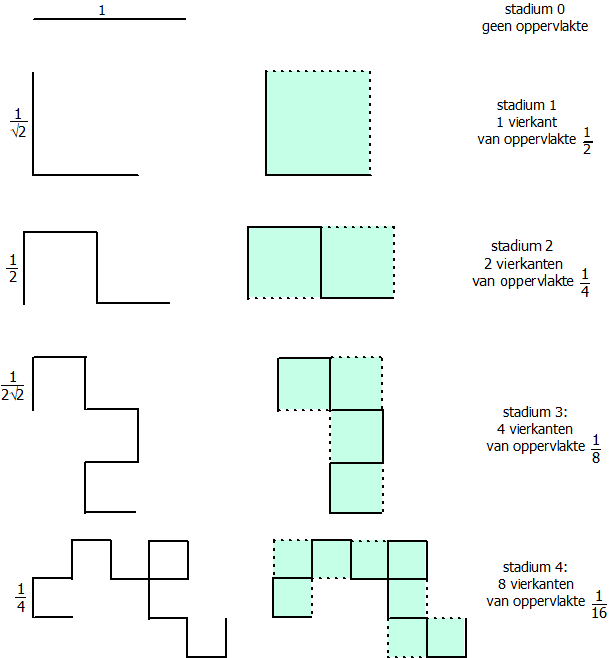
Laten we voor een aantal stadia van de draakkromme eens kijken hoeveel vierkantjes er nodig zijn om hem te bedekken, en hoe groot zijn oppervlakte dus is. We bedekken de draakkromme met vierkantjes door vanaf het begin steeds de lijnstukjes per paar te bekijken en elke keer het vierkant te tekenen dat bij dat paar lijntjes hoort.
       

       
Je ziet:  bij elke volgende stap verdubbelt het aantal benodigde vierkantjes, maar hun oppervlakte halveert (zijden keer 1/√2).  De totale oppervlakte blijft dus constant en is gelijk aan 1/2.
       
Een vlakvulling.
       
Je kunt met de draakkromme het hele vlak vullen want er passen rond een punt steeds vier draakkrommen in elkaar, zoals je ziet aan het prachtige borduurwerkje hieronder.
       

Bron:  http://larryriddle.agnesscott.org/ifs/heighway/heighwayCrossStitch.htm
       
De huid van de draak.
       
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)