© h.hofstede (h.hofstede@hogeland.nl)

Het chaos-spel.

     
Er is nog een hele vreemde andere manier om een fractal te produceren, en dat is door het chaos-spel.

Ik zal voordoen hoe het werkt aan de hand van de Sierpinski driehoek die je hiernaast ziet en die we in deze les al eerder tegenkwamen.
       
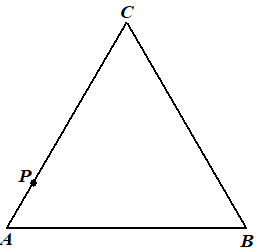
Het spel is heel eenvoudig en gaat als volgt.
Teken eerst een gelijkzijdige driehoek ABC en kies ergens een punt P op deze driehoek:
       

       
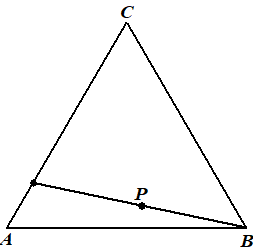
Kies nu willekeurig één van de drie hoekpunten, en teken een nieuw punt P dat halverwege het eerste punt P en het gekozen hoekpunt ligt. Bij de keuze van hoekpunt B zou dat dit opleveren:
       

       
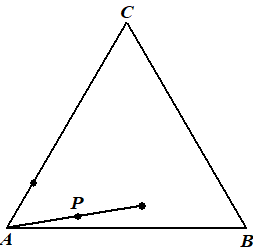
Kies weer willekeurig een hoekpunt en teken het volgende punt P halverwege het laatste punt P en dat gekozen hoekpunt.  Neem bijvoorbeeld hoekpunt A, dan zou dat dit opleveren:
       

       
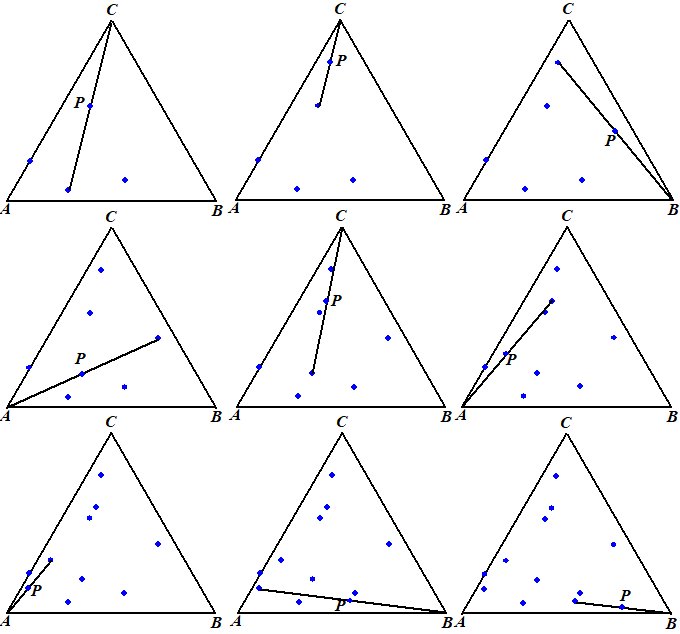
Ga zo alsmaar door!
Hier zie je nog negen volgende stappen in leesvolgorde (de getekende lijn laat zien welk hoekpunt gekozen is).
       

       
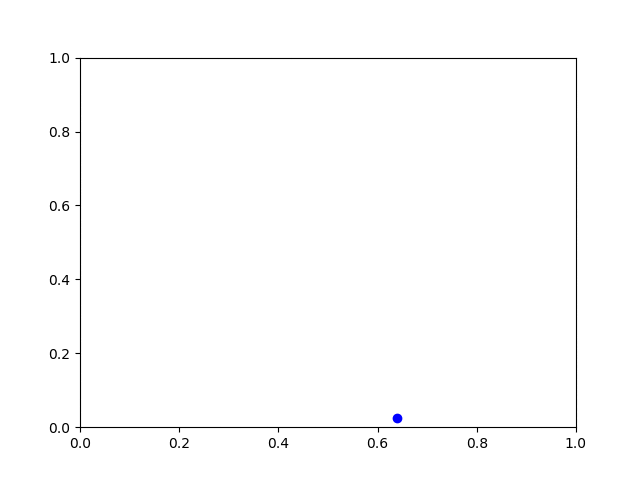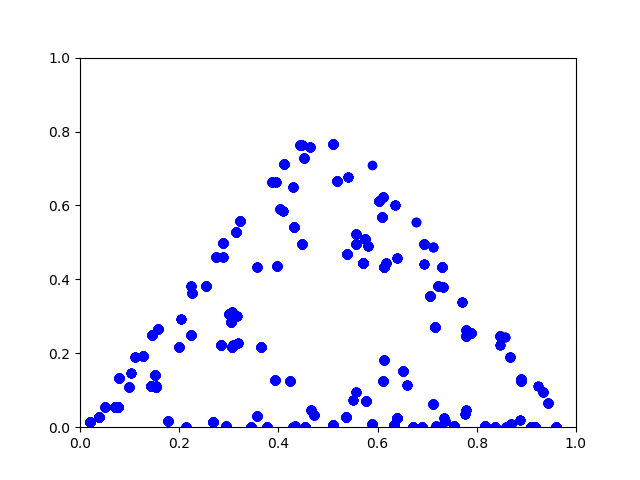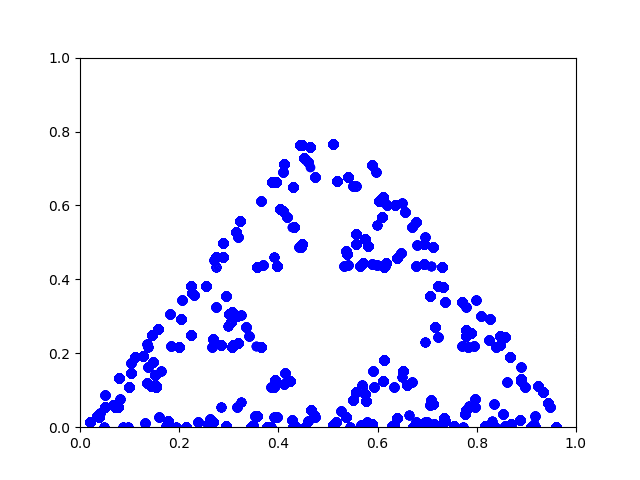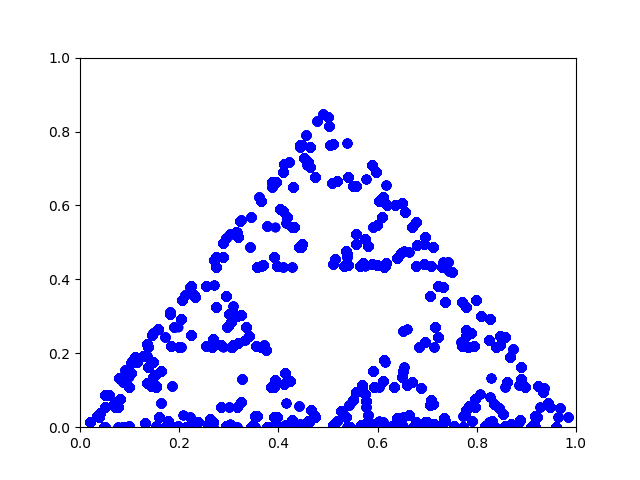
Nou, als je hier alsmaar mee doorgaat dan zie je zoiets verschijnen:
       

BRON:  https://www.johndcook.com/blog/2017/07/08/the-chaos-game-and-the-sierpinski-triangle/
       
WAUW!!!
Dat nadert steeds meer naar de Sierpinski-driehoek!
Hoe kan dat?..........
       
JA! Hoe kan dat?
       
Dat kun je het best inzien door te beginnen met een gelijkzijdige driehoek. Daarna kijk je waar de middelste witte driehoek (die dus NIET bij de Sierpinski driehoek hoort) op wordt afgebeeld:
       

       
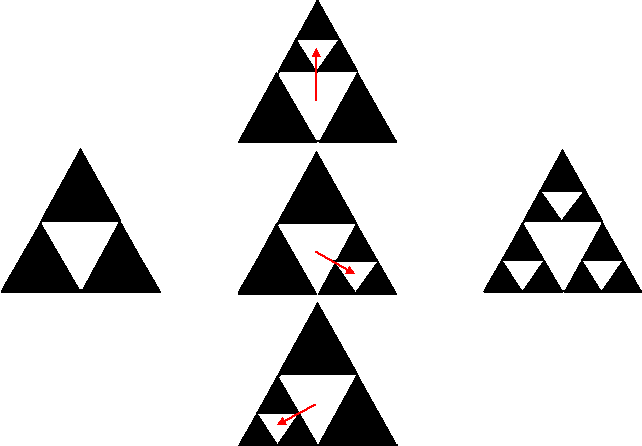
Die middelste witte driehoek gaat (al naar gelang de keuze van het hoekpunt), naar één van de andere witte driehoeken uit de volgende stap van de Sierpinski-driehoek. Zie de figuur.
En bij de volgende stap gebeurt hetzelfde!
Elke witte driehoek wordt afgebeeld op een kleinere witte driehoek uit de volgende Sierpinski-stap. Kijk maar:
       

       
En dat gaat zo alsmaar door!!
Maar als witte driehoeken alsmaar afgebeeld worden op witte driehoeken, dan worden automatisch zwarte driehoeken ook afgebeeld op zwarte driehoeken. Elke nieuwe zwarte stip is dus een deel van de Sierpinski-driehoek, en als dat er oneindig veel worden, dan verschijnt vanzelf de fractal.

Wil je dit met eigen ogen op je TI-rekenmachine zien?
Gebruik dan dit programmaatje.
       

       
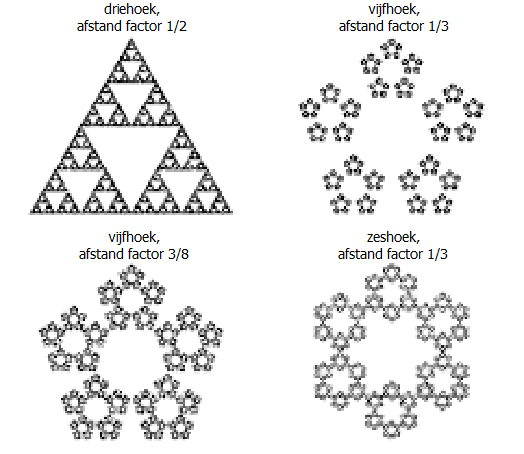
Door in plaats van met een driehoek met een andere veelhoek te beginnen kun je andere fractals krijgen.  Je kunt ook variatie maken door bijvoorbeeld de afstand tot de hoekpunten niet steeds te halveren, maar bijvoorbeeld 1/3 deel te maken.
Hier zie je een paar fractals die allemaal uit één of ander Chaos-spel zijn ontstaan:
       

       
Bij die laatste zien we daar binnenin (de rand van het binnenste gedeelte van de zeshoek) een oude bekende. 
Nee maar! 
Daar heb je de Koch-sneeuwvlok!!!

Trouwens, bij een vierkant werkt het niet! Dat wordt langzaamaan gewoon helemaal gevuld, en produceert geen fractal. Je kunt wel een fractal in een vierkant krijgen door de keuze van het hoekpunt te beperken. Als je bijvoorbeeld eist dat het zelfde hoekpunt nooit twee keer achter elkaar gekozen kan worden (dus dat je steeds een ander hoekpunt moet kiezen), dan krijg je zoiets:
       

       
En als je eist dat het volgende hoekpunt nooit één plaats (tegen de klok in) vanaf de huidige mag zijn, dan levert dat dit op:
       

       
Op de volgende site kun je het chaosspel zelf spelen met veelhoeken met verschillende aantallen hoekpunten, en bij elk hoekpunt variërende kansen.
Veel speelplezier!!!
       
       
De varen van Barnsley.
       
In de Sierpinski-driehoek zag je hoe uit een punt P een volgend punt P gemaakt wordt, door de afstand tot een willekeurig gekozen hoekpunt te halveren.
Stel dat de driehoek hoekpunten  (0,0) en (1,0) en (1/2, 1) heeft.
Dan komt dat kiezen van een volgend punt P eigenlijk neer op één van de volgende transformaties: 
       
xn + 1 =  1/2 • xn
yn +  1 = 1/2 • yn
Voor  het hoekpunt rechtsonder.		 xn + 1 = 1/2 • (1/2 + xn)
yn + 1 = 1/2 • (1 + yn)
Voor het hoekpunt boven.		 xn + 1 = 1/2 • (1 + xn)
yn + 1 = 1/2 • yn
Voor het hoekpunt linksonder.
       
Door andere transformatieformules te nemen kun je andere fractals maken.
De wiskundige Michael Barnsley begon met een punt (0, 0) en gebruikte vervolgens steeds willekeurig één van de volgende vier transformaties:
       
xn + 1 = 0
yn + 1 = 0,16 • yn		 xn + 1 = 0,85xn + 0,04yn
yn + 1 = -0,04xn + 0,85yn + 1,6 		xn + 1 =  0,2xn - 0,26yn
yn + 1 = 0,23xn + 0,22yn + 1,6		 xn + 1 = -0,15xn + 0,28yn
yn + 1 = 0,26xn + 0,24yn + 0,44
       
Hij plugde dit in zijn computer, drukte op PLAY en zag de volgende prachtige figuur verschijnen:
       

       
       

© h.hofstede (h.hofstede@hogeland.nl)