| |
 |
| De
Discriminant. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
| Laten we nog even samenvatten wat we tot nu
toe hebben gevonden over kwadratische vergelijkingen: |
|
|
|
Schrijf de vergelijking eerst in de
vorm
ax2 + bx + c = 0
Dan zijn er twee oplossingen: |
| |
|
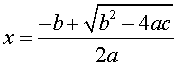 |
 |
|
|
|
|
Geen vuiltje aan de lucht! Even invullen en
klaar! Twee antwoorden. Volgende som.
Helaas.....Er kan iets fout gaan. Neem bijvoorbeeld de
vergelijking 3x2 + 5x + 8 = 0
dan is b2 - 4ac = 52
- 4•3•8 =
-71. En √(-71) kun je niet berekenen
want je kunt niet de wortel uit een negatief getal trekken. Kortom;
altijd als b2 - 4ac < 0 dan geeft de
ABC-formule geen oplossingen!
En ook als b2 - 4ac precies gelijk is aan nul
is er iets aparts aan de hand: de bovenstaande twee oplossingen geven
het zelfde antwoord, immers er staat in de ene dan +√0
en in de andere -√0 maar dat is allebei toch
nul.
Dus als b2 - 4ac = 0 dan is er precies één
oplossing van de vergelijking.
Die b2 - 4ac bepaalt (determineert)
dus eigenlijk hoeveel oplossingen een kwadratische vergelijking heeft.
Hij heet daarom de DISCRIMINANT van de vergelijking. We gebruiken
ervoor de letter D.
Samengevat: |
|
|
|
Discriminant = D = b2
- 4ac
D > 0 : twee oplossingen
D = 0 : één
oplossing
D < 0 : geen oplossingen |
|
|
|
| 1. |
Los op: |
|
a. |
3x2 + 6x + 6
= 0 |
|
e. |
(x + 2)(x + 3) = x |
|
|
b. |
x2
- 5x + 8 =
0 |
|
f. |
x2 + x = -0,25 |
|
|
c. |
8x2 = 2x + 5 |
|
g. |
x(x - 5) = 24 |
|
|
d. |
12x2 = 9x
- 4 |
|
h. |
x2
- 10x + 50
= 10x - x2 |
|
|
|
|
| 2. |
Iemand beweert:
"Als a en c tegengesteld van teken zijn, dan zijn er
altijd twee oplossingen"
Leg uit of dat inderdaad altijd zo is.
Iemand anders beweert: ""Als er twee
oplossingen zijn dan zijn a en c verschillend van teken"
Leg uit of dat inderdaad zo is. |
|
|
|
|
|
|
| Wat betekent dat voor
een probleem? |
|
|
Flauwe opmerking: Dat hangt ervan af wat we
aan het uitrekenen zijn!
Meestal komt een kwadratische vergelijking tevoorschijn als we
snijpunten van twee grafieken aan het berekenen zijn of snijpunten met
de x-as van een parabool: |
|
| geval A: de nulpunten
van een parabool. |
|
|
De nulpunten van een parabool zijn de x-coördinaten
van de snijpunten met de x-as. Die vinden we door de formule van
een parabool gelijk aan nul te tellen, dus dat geeft een kwadratische
vergelijking.
• Als van die vergelijking D > 0 dan heeft de parabool dus
twee snijpunten met de x-as.
• Als D = 0 dan is er één snijpunt met de x-as (hij
ligt tegen de x-as aan, ofwel hij raakt de x-as.
• Als D < 0 dan heeft de parabool helemaal geen snijpunten
met de x-as, dus dan ligt hij er in zijn geheel boven of onder.
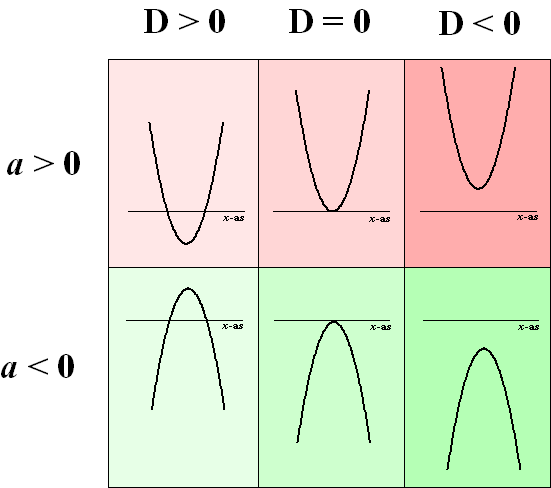
Als we verder bedenken dat het getal a dat voor het kwadraat
staat bepaalt of we te maken hebben met een dalparabool (a
> 0) of een bergparabool (a < 0) dan hebben
we al direct een aardig idee over de ligging van de parabool.
In de volgende figuur zie je zes mogelijkheden systematisch
gerangschikt. |
|
|
|
|
|
|
| geval B: de snijpunten van
twee grafieken. |
|
|
Ook als je twee grafieken met elkaar snijdt
(bijvoorbeeld een parabool met een rechte lijn of twee parabolen met
elkaar) krijg je een kwadratische vergelijking. Die moet je dan eerst op
nul herleiden, en ook dan kun je van de resterende vergelijking de
discriminant uitrekenen. Bedenk dat elke x die je vindt de x-coördinaat
van een snijpunt is.
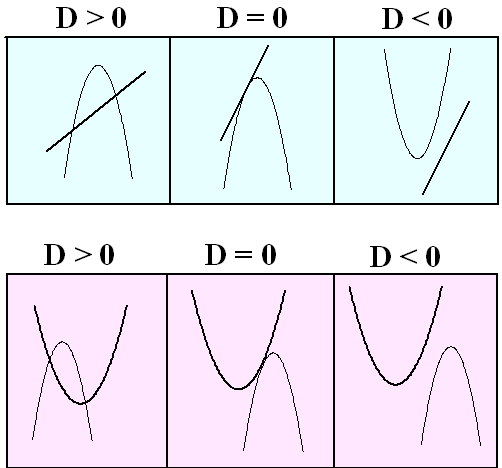
• Als D > 0 zijn er twee oplossingen dus ook twee snijpunten
• Als D = 0 is er één oplossing en dus ook één snijpunt. De
grafieken raken elkaar dan meestal.
• Als D < 0 zijn er geen oplossingen dus ook geen snijpunten.
De volgende figuur verduidelijkt één en ander. |
|
|
|
|
|
|
| 3. |
Hoeveel snijpunten hebben de volgende grafieken? |
|
a. |
De lijn y = 2x
- 4 en de
parabool y = 4x2 + 3x
- 6 |
|
|
b. |
De parabolen y = 5x2
+ 200x + 700
en y = 38x - 4x2
- 29 |
|
|
c. |
De parabool y = 2x2
- 11x + 4 en de lijn y = -12 |
|
|
|
|
| 4. |
Op tijdstip t = 0 is de
situatie op een autoweg als volgt: |
|
|
|
|
 |
|
|
|
|
Auto A rijdt met een snelheid van 144
km/uur, maar is aan het afremmen omdat hij vóór
zich een andere auto ziet. Voor de afstand van de voorkant van
zijn auto tot het punt waar hij zich nu bevindt, laten we het
punt P noemen, geldt de formule S(t) = 40t
- t2
Die andere auto, auto B rijdt op een afstand van 60 meter vóór
auto A met een snelheid van 72 km/uur, maar is aan het
optrekken. Voor de afstand van de achterkant van zijn auto tot P
geldt S(t) = 0,5t2 + 20t +
60 |
|
|
|
| |
Onderzoek of de auto's een botsing
zullen krijgen. |
| |
|
| |
|
| 5. |
Gegeven zijn de parabolen: y = x2
- 4x + 5 en y = 2x
- 2x2
+ 2
Onderzoek of deze twee parabolen elkaar raken of
niet.
|
| |
|
 6. 6. |
Olympiadevraagstuk.
Als ax2 + 2bx + c = 0 twee gelijke
oplossingen heeft, dan is het rijtje a - b
- c
een meetkundig rijtje.
(dat betekent dat tussen a naar b dezelfde
vermenigvuldigingsfactor zit als tussen b en c)
Bewijs dat! |
| |
|
| |
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
|
|
|
|
|
|
|
|
|
|