| |
 |
| |
ę h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Cyclo´den |
| |
|
|
|
Cyclo´den zou je grofweg kunnen
omschrijven als "Banen die ontstaan door cirkelbewegingen".
Dat klinkt nogal simpel, maar kan toch best interessant worden, vooral
als een punt aan meerdere cirkelbewegingen tegelijk deelneemt. In deze
les zullen we formules voor zulke banen gaan opstellen. |
| |
|
|
|
Handig Hulpje.
Eerst maar even een handig hulpje, en dat is het volgende:
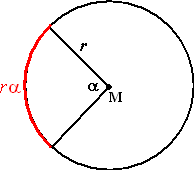
"Als je van een cirkel met straal r een deel van de omtrek neemt dat
hoort bij middelpuntshoek
α, dan is de
lengte daarvan rα"
Dat hoort bij de figuur hiernaast. De hele omtrek is 2πr
en die hoort bij hoek 2π
radialen, dus bij hoek
α hoort 2πr
Ľ
α/2π
= rα |
 |
| |
|
|
|
|
1. De Cyclo´de |
| |
|
|
|
| Als een wiel met straal
1 en snelheid 1 over een vlak oppervlak rolt, dan beschrijft
een punt op de omtrek van dat wiel een parameterkromme die
cyclo´de heet. Dat ziet er ongeveer zˇ uit (de rode lijn): |
| |
|
|
|
|
 |
| |
|
|
|
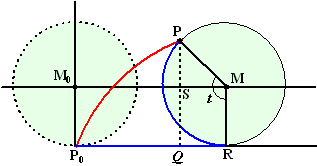
In de situatie
hiernaast is de oorsprong P0. Na t seconden is
dat punt in P aangekomen en heeft het de rode baan doorlopen.
Omdat de blauwe stukken gelijk zijn aan elkaar geldt dat
P0R = t
en
dus is ook boog PR = t
dus ook ∠RMP = t
Laten we de x-co÷rdinaat en de y-co÷rdinaat van P apart
berekenen.
Bedenk dat ∠SMP = t -
1/2π
en gebruik sos-cas-toa in
driehoek MSP
xP = PR - QR
= PR - MS
= t - cos(t - 1/2π)
= t - sint |
 |
| |
|
|
|
yP
= SQ + SP
= MR + SP
= 1 + sin(t - 1/2π)
= 1 - cost |
|
| |
|
|
|
| Daarmee hebben we de
parametervergelijkingen voor de cyclo´de gevonden. Als de straal
niet 1 is, maar r, dan wordt alles gewoon met r
vermenigvuldigd. Verder maakt de snelheid natuurlijk niets uit voor de
vorm van de baan (alleen komen er dan bij elk punt andere
t-waarden). |
| |
|
|
|
|
|
| |
|
|
|
| De cyclo´de is een
beroemde figuur uit de geschiedenis van de wiskunde. Het (zij?) wordt
wel de "Helena van de Geometrie" genoemd. Meer
daarover in de volgende twee lessen. |
| |
|
|
|
| |
|
|
|
| 1. |
a. |
In 2π
seconden maakt het wiel ÚÚn omwenteling.
Bereken de lengte van de baan die punt P dan heeft afgelegd. |
| |
|
|
|
| |
Het feit dat er zo'n mooi rond getal
uit deze lengte komt doet ons vermoeden dat we de lengte
misschien ook wel algebra´sch zouden kunnen berekenen.
Voor de snelheid v geldt v(t) =
√(2 - 2cost) |
| |
|
|
|
| |
b. |
Toon dat aan. |
|
| |
|
|
|
| |
Een primitieve van
√(1 - cost) voor x
tussen 0 en
π is -2√(1
+ cost) |
| |
|
|
|
| |
c. |
Toon dat aan door deze primitieve te
differentiŰren. Leg ook uit waarom deze primitieve alleen geldt
voor x tussen 0 en
π. |
| |
|
|
|
| |
d. |
Bereken met deze primitieve de
lengte van de baan van P gedurende ÚÚn omwenteling algebra´sch. |
| |
|
|
| |
e. |
Toon aan dat de lengte
van de baan gelijk is aan 8r waarbij r
de straal van de cirkel is. |
| |
|
|
| |
|
|
| 2. |
Toon aan dat de
oppervlakte onder ÚÚn zo'n boog gelijk is aan 3πr2
waarbij r de straal van de cirkel is. |
| |
|
|
|
|
| |
|
|
|
|
2. De Hypocyclo´de. |
| |
|
|
|
Het wordt natuurlijk nog leuker
als we cirkels langs cirkels laten rollen.....
De hypocyclo´de is de kromme die wordt beschreven door een punt P dat op de
omtrek van een kleinere cirkel ligt die langs de binnenkant van
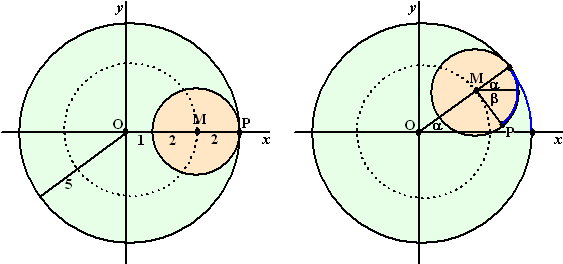
een grotere cirkel rolt. Laten we een cirkel met straal 5
en middelpunt M nemen waarlangs een cirkel met straal 2 en
middelpunt N rolt. Op tijdstip t = 0 is de situatie als
links hieronder getekend. |
| |
|
|
|
|
 |
| |
|
|
|
Als de draaihoek
a is dan is de blauwe booglengte langs de grote cirkel in
de figuur rechts gelijk aan 5a.
Maar dan is de blauwe booglengte langs de kleine cirkel ˇˇk
gelijk aan 5a omdat die stukken langs
elkaar zijn gerold. Punt P is ten opzichte van M gedraaid over
een hoek
α +
β
en dat is 21/2α,
zodat
β = 11/2α.Met xAB bedoelen
we voortaan: de x co÷rdinaat
van A ten opzichte van B (dus xA - xB)
Voor de x-co÷rdinaat van P geldt dan xP
= xPO = xMO + xPM
xMO
= xM = 3cosα (de
gestippelde cirkel heeft straal 3)
trek een lijnstukje van P loodrecht omhoog, dan geldt: xMP
= 2cosβ = 2cos(11/2α)
Daaruit volgt xP = 3cosα
+ 2cos(11/2α)
Voor de y-co÷rdinaat
van P vinden we op precies dezelfde manier yP = 3sinα
- 2sin(11/2α).
Ga dat zelf maar na.
Als we tenslotte de stralen 5 en 2 van de cirkels vervangen door R
(straal grote cirkel) en r (straal klein cirkel) dan geeft dat de
algemene vergelijking voor de hypocyclo´de; |
| |
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| 3. |
Neem de kromme uit het voorbeeld, dus met
stralen 5 en 2. |
| |
|
|
|
| |
a. |
Toon aan dat de periodes van x(α)
en y(α) beiden gelijk zijn aan
4π, dus de periode van kromme K ook. |
| |
|
|
|
| |
b. |
Leg uit hoe je met de afmetingen van
de cirkels al kunt beredeneren dat K vijf keerpunten zal hebben.
Bereken vervolgens met de vergelijkingen van K de co÷rdinaten
van de keerpunten. |
| |
|
|
|
| |
c. |
Schets kromme K. |
| |
|
|
|
| |
|
|
|
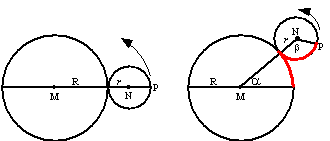
| 4. |
Een cirkel kan natuurlijk ook om een andere
cirkel heen rollen, zoals je hiernaast ziet. De kromme die punt
P dan beschrijft heet een epicyclo´de. |
 |
| |
|
|
| |
a. |
Kies M als oorsprong en
geef een parametervergelijking voor de kromme die punt P
beschrijft. Bedenk daarbij dat die rode cirkeldelen even lang
zijn. |
| |
|
|
|
| |
b. |
Als R =
r dan heet deze epicyclo´de een cardio´de.
Plot die cardio´de. |
| |
|
|
|
| |
c. |
Als R = 2r
dan heet deze epicycloide een nefro´de.
Plot die nefro´de. |
| |
|
|
|
| |
|
|
|
|
|
3. Meerdere Cirkelbewegingen. |
| |
|
|
|
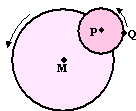
Op een kermis staan
vaak draaimolens die bestaan uit een grote arm die ronddraait en waaraan
een kleinere bakjes is vastgemaakt die ˇˇk om zijn middelpunt draait.
Zie de figuur hiernaast.
Wiskundig gezien kunnen we dit zien als een punt P dat in een cirkelbaan
om M draait, terwijl een punt Q weer in een kleinere cirkel om P draait. |
 |
| |
|
|
|
 |
| |
|
|
|
| Neem als oorsprong punt M. Stel
dat de grote cirkel straal 8 meter heeft en ronddraait in 20 seconden en
dat de kleine cirkel straal 3 meter heeft en dat Q om P draait in
5 seconden. Laat P en Q op tijdstip t = 0 op de positieve x-as
beginnen. Dan is de situatie als volgt: |
| |
|
|
|
|
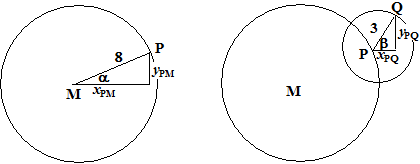 |
| |
|
|
|
Als de grote cirkel 2π
radialen in 20 seconden draait, dan geldt voor de draaihoek:
α = 2π/20t
= 0,1πt
In de linkerfiguur hierboven zie je dat dan geldt xPM
= 8cosα = 8cos(0,1πt)
en yPM = 8sinα =
8sin(0,1πt)
Als de kleine cirkel 2π radialen in 5
seconden draait, dan geldt voor de draaihoek ten opzichte van P:
β = 2π/5t
= 0,4πt. In de rechterfiguur
hierboven zie je dat dan geldt xPQ = 3cosβ
= 3cos(0,4πt) en yPQ = 3sinβ = 3sin(0,4πt)
Maar voor de x coordinaat van Q ten opzichte van M
geldt:
xQ = xPM + xPQ = 8cos(0,1πt)
+ 3cos(0,4πt)
(merk nog even op dat die cos er meteen rekening mee houdt of xPM
en xPQ positief of negatief zijn!)
En voor de y -co÷rdinaat van Q ten opzichte van M geldt op
dezelfde manier: yQ = 8sin(0,1πt)
+ 3sin(0,4πt)
samen geeft dat: |
|
|
| |
|
|
|
| |
|
|
|
| 5. |
a. |
Bereken de maximale baansnelheid van punt Q |
| |
|
|
|
| |
b. |
Bereken de afstand die punt Q in ÚÚn periode aflegt. |
| |
|
|
|
| |
c. |
Plot de baan van Q. |
| |
|
|
|
|
| |
|
|
|
| |
|
|
 |
|
ę h.hofstede (h.hofstede@hogeland.nl)
|