 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| Complexe
getallen in vlakke meetkunde. |
|
|
In de "gewone" meetkunde kun je toch vaak gebruik
maken van complexe getallen.
Hier zijn een aantal gevallen.
|
|
|
| 1. Bewijs dat lijnen AB en
CD loodrecht op elkaar staan |
| |
Noem de hoekpunten de complexe getallen a,
b, c en d
Dan staat AB loodrecht op CD als (a
- b)/(c
- d ) geheel imaginair is. |
| |
|
| |
Bewijs.
De vector BA kun je voorstellen door het complexe getal z1
= a - b
De vector DC kun je voorstellen door het complexe getal
z2 = c - d
z1 en z2 staan loodrecht
op elkaar als z1 uit z2
ontstaat door draaiing over Ī90į
Dat is hetzelfde als
vermenigvuldigen met Ī
pi . Dus z1 = piz2
dus is z1/z2 = pi
en dat is geheel imaginair. |
|
|
|
|
| |
| |
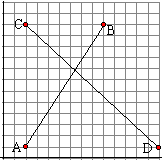
Voorbeeld.
A = (2,1) en B = (9, 12) en C = (2, 12)
en D = (14,1)
a - b = 2 + i - 9 - 12i = -7
- 11i
c - d = 2 + 12i - 14 - i = -12
+ 11i
(a - b)/(c -
d) = (-7 - 11i)/(-12 +
11i) ≈ -0,14 +
0,79i
Dat is niet geheel imaginair dus de lijnen staan
niet loodrecht op elkaar. |
 |
|
| |
| 2. Bewijs dat de lijnen AB
en CD evenwijdig zijn |
|
Noem de hoekpunten weer de complexe getallen a,
b, c en d.
Dan zijn AB en CD evenwijdig als geldt: dat (a
- b)/(c - d ) geheel
reŽel is. |
|
|
| 3. Bewijs dat twee driehoeken ABC
en DEF gelijkvormig zijn. |
|
Noem de hoekpunten de complexe getallen a,
b, c, d, e en f
Dan zijn er twee mogelijkheden als de driehoeken
gelijkvormig zijn:
(b - a)/(c - a)
= (e - d )/(f - d )
of (b - a)/(c -
a) = (e" - d")/(f"
- d")
Met a" wordt de geconjugeerde van a bedoeld.
In het eerste geval hebben de driehoeken dezelfde oriŽntatie,
in het tweede geval niet. |
|
|
|
|