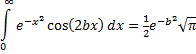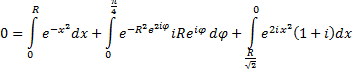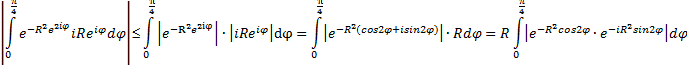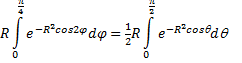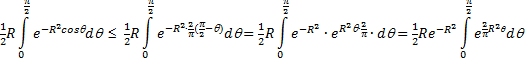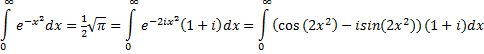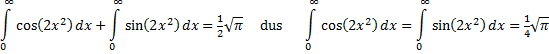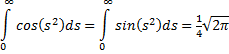Integraal van Cauchy en Fresnel


	© h.hofstede (h.hofstede@hogeland.nl)

Een beroemde integraal van Cauchy.

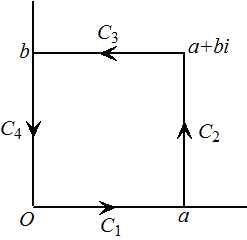
Bekijk de integraal van f(z) = e^-z² op de route hiernaast.
Die bestaat uit 4 delen C₁, C₂, C₃, C₄.
e^-z^² = e^{-(x + iy)²} = e^-x^{² - 2ixy
+ y²} = e^-x^{²
+ y²} • e^-2ixy
= e^-x² • e^y²• (cos2xy - isin2xy)
Splitsen in een reëel deel en een imaginair deel:

f(z) = u + iv met
u(x, y) = e^-x^² • e^y² • cos2xy
v(x, y) = -e^-x^² • e^y² • sin2xy

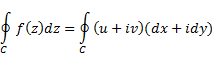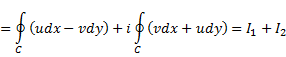Laten we dit gaan integreren over de routes C₁ tm C₄

C₁

y = 0 dus dy = 0 dus u = e^-x² en v = 0

C₂

x = a en dx = 0 dus u = e^-a^² e^y^² cos2ay en v = -e^-a² e^y^²sin2ay

C₃

y = b en dy = 0 dus u = e^-x² e^b^²cos2bx en v = -e^-x²e^b^²sin2bx

C₄

x = 0 en dx = 0 dus u = e^y^² en v = 0

Eerst rekenen we nu het reële deel van de kringintegraal (dat is dus integraal I₁ hierboven) uit.
Dat geeft:

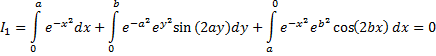Dat dat nul is, dat komt door de kringintegraal van Cauchy: als die hele integraal nul is, dan moeten zowel het reële als het imaginaire deel apart van elkaar nul zijn. Dus I₁ = 0 en I₂ = 0
Je kunt deze drie integralen herrangschikken (met nog wat grenzen wisselen) tot:

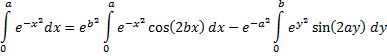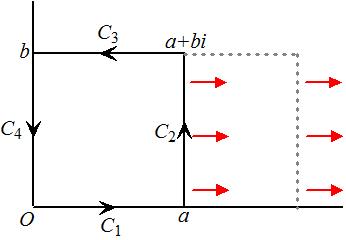
En nou gaan we weer iets leuks doen: we gaan de rechterkant van de rechthoek steeds verder naar rechts schuiven. Dus a → ∞ en de rechthoek verandert in een oneindig brede strook met hoogte b.
Wat gebeurt er dan met de integralen?

Van die eerste twee veranderen alleen de grenzen. Die derde integraal gaat naar nul, want e^-a² gaat naar nul en sin(2ax) blijft een getal tussen 0 en 1.

Dat geeft het volgende resultaat:

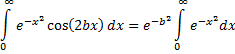En daar helemaal aan de rechterkant staat een beroemde integraal! Het is de Gauss-integraal (die van de normale verdeling weet je nog?) en we weten al dat die gelijk is aan ¹/₂√π (staat in deze les). Daarmee hebben we een prachtig nieuw resultaat geboekt:

Geweldig toch? Nu hebben we een schijnbaar onmogelijk moeilijke integraal voor reële getallen uitgerekend door gebruik te maken van de kringintegraal van Cauchy in het complexe vlak!!

Een beroemde integraal van Fresnel.

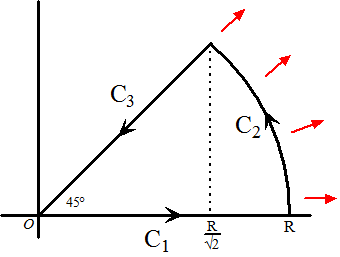
Laten we nu dezelfde complexe functie f(z) = e^-z²nog een keer integreren maar nu via een andere integratieroute.
Neem als route de taartpunt hiernaast.

Voor deel C₁ geldt z = x en x loopt van 0 tot R en dz = dx

Voor deel C₂ geldt: z = Reⁱ^φ en φ loopt van 0 tot ^π/₄. Verder is dan dz = iRe^iφ dφ

Voor deel C₃ geldt: z = x + iy = x + ix (want het is de lijn y = x in het reële vlak). Dus dz = (1 + i)dx en x loopt van ^R/_√2 naar 0.

Samen geeft dat een totale kringintegraal die nul moet zijn, dus:

Wat gebeurt er als we R naar oneindig laten gaan, net zoals bij de integraal van Cauchy?
Dan wordt die middelste integraal gelijk aan nul. Kijk maar:

Daarbij is weer gebruikt dat |z₁ • z₂| ≤ |z₁| • | z₂|. Bij die eerste stap eigenlijk direct al twee keer: eerst om de modulus binnen de integraal te zetten (een integraal is een som) en daarna nog eens om die integrand te splitsen in twee delen. Verder weten we dat |e^ix|= 1, dat is bij de tweede stap gebruikt.

Als je hetzelfde doet bij die laatste integraal (splitsen in twee stukken en de modulus van dat stuk met e^i... wordt 1) dan hou je eigenlijk alleen nog over:

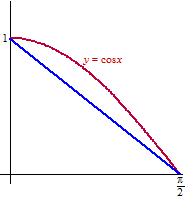
(Daarbij ben ik stiekem overgestapt op een nieuwe variabele θ = 2φ)

Hiernaast zie je dat je tussen 0 en ^π/₂ de grafiek van cosx groter is dan de blauwe lijn, en dat is de grafiek van y = ²/_π • (^π/₂ - x).
Maar dan is e^-R^²^cosx ≤ e^-R²
y

Dat geeft voor de integraal:

primitiveren en invullen:

en dat gaat inderdaad naar nul als R naar oneindig gaat.

Dus blijven alleen de eerste en de laatste integraal over, waarbij die eerste weer een oude bekende is (weer die Gauss-integraal van hierboven), dus dat geeft samen (met R naar oneindig):

Omdat daar kennelijk dus ¹/₂√π moet uitkomen moet het reële deel gelijk zijn aan ¹/₂√π en het imaginaire deel gelijk aan 0. Het reële deel geeft:

Daarbij is gebruikt dat die beide integralen gelijk zijn (omdat het imaginaire deel nul moet worden). Schakel nu over naar de variabele s² = 2x², dan is 2sds = 4xdx en dat geeft voor de integralen het volgende prachtige resultaat: