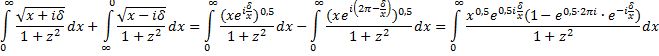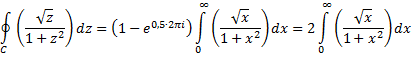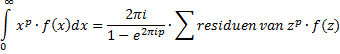meerwaardige complexe functies


	© h.hofstede (h.hofstede@hogeland.nl)

Meerwaardige Functies.

We zijn hiervoor in de lessen over complexe getallen op twee plaatsen al meerwaardige complexe functies tegengekomen:

•

Bij niet-gehele machten.
Zo zagen we al dat √z bestaat uit twee waarden, en ³√z uit drie waarden, enz......
In het algemeen had de vergelijking zⁿ = p in totaal n oplossingen die mooi op de hoekpunten van een regelmatige n-hoek lagen, weet je nog?

•

Bij logaritmen
Als e^p = z dan is ook e^p^{+ 2πi} = z
maar omdat e^p = z de oplossing is van lnz = p betekent dat, dat lnz de waarden p + 2πi aanneemt. Dat zijn zelfs oneindig veel waarden (op afstand 2πi van elkaar)

Dat meerwaardig zijn heeft nogal gevolgen voor integralen.
Stel bijvoorbeeld dat we de functie f(z) = √z bekijken en dat we besloten hebben dat √(-1) = i (en om één of andere reden niet de waarde -i). Als de functie f analytisch is, dan zal vlak naast het punt z = -1 die √z een waarde in de buurt van i hebben. Zo'n analytische functie kan immers geen rare sprongen maken.

Als je dan √z langs de eenheidscirkel "volgt", bijvoorbeeld omdat dat de gekozen integratieroute is, dan krijg je zoiets:

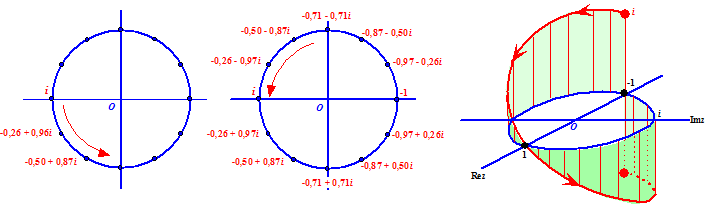
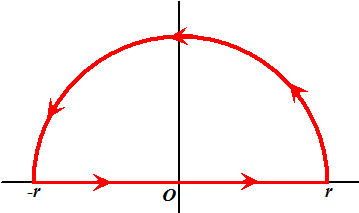
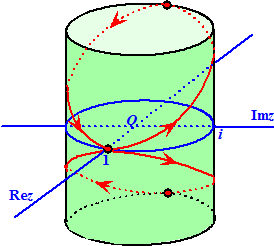
In de linker figuur zijn we vanaf punt z = -1 (we hebben gekozen √-1 = i) tegen de klok in langs de eenheidscirkel gaan bewegen. 30º verder ligt het punt z = -0,5√3 - 0,5i en daarbij zijn twee mogelijkheden voor √z, namelijk -0,26 + 0,86i en 0,26 - 0,86i. Maar als de functie √z analytisch moet zijn, dan moeten we nu wel de eerste nemen (rare sprongen mogen niet!).
In de middelste figuur zijn we zo de hele eenheidscirkel rondgegaan.
Als je dat doet, dan kom je uiteindelijk weer bij z = -1 uit, maar dan heb je √z = -i, en dat is niet gelijk aan de oorspronkelijke i. Het past niet aan elkaar!!!

Rechts staat het imaginaire deel van √z getekend met z rond de eenheidscirkel. Je ziet dat er een sprong tussen de uiteinden van die rode spiraal zit van -i naar +i. Dat betekent dat de functie als je met een integraal het punt z = -1 passeert, een sprong vertoont en dus niet analytisch is.

(voor het reële deel geldt precies zo'n zelfde verhaal, maar ik kan er nou eenmaal niet meer dan één tegelijk tekenen, want ik heb helaas niet meer dan 3 dimensies tot mijn beschikking

Als je gewoon doorgaat vanaf z = -1 dan vind je voor het imaginaire deel van √z zoiets als hiernaast.
Na twee rondjes om de eenheidscirkel is het imaginaire deel van √z wél weer aanbeland bij de beginwaarde.

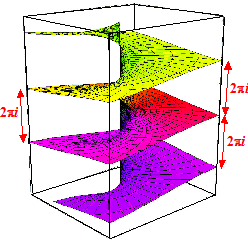
Bij lnz geldt het zelfs nog erger; de grafiek daarvan bestaat uit allemaal verschillende "plateaus" op afstand 2pi van elkaar.

Hiernaast zie je een impressie. Als je rondjes draait zul je steeds van het ene naar het andere plateau springen!

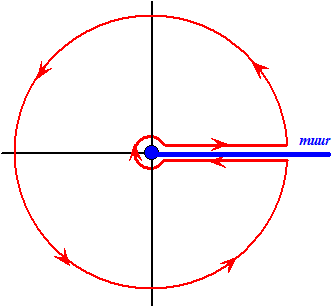
Hoe lossen we dat "meerwaardigheidsprobleem" op?

Op de eenvoudigste manier: we verbieden gewoon dat een route waarlangs we integreren een heel rondje draait. Dat doen we door kunstmatig ergens een muur op te bouwen: een lijn waar de integratieroute niet overheen mag gaan. Hieronder zie je vier veel voorkomende gevallen van zo'n verboden grensovergang. de rode lijn mag steeds niet gepasseerd worden.

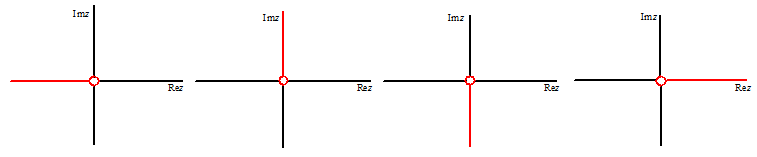Natuurlijk mag zo'n barrière ook best schuin lopen, maar de berekeningen zijn wat eenvoudiger als je één van bovenstaande vier voorbeelden kiest.

Uitgebreid Voorbeeld.

Kies bijvoorbeeld de integratieroute hiernaast, en laat r naar oneindig gaan, zou je zeggen.....

Maar wacht eens even.... Mag dat eigenlijk wel???

Nou nee......

Die √x is meerwaardig.
Dus als je ergens op de route begint en dan een heel rondje draait, dan kom je uit bij een nieuwe waarde die een sprong maakt vergeleken met de oorspronkelijke beginwaarde, dus als je die integraal "sluit" dan maak je een sprong en is de functie niet analytisch, dus mag je Cauchy niet gebruiken.

Je moet zo'n "muur" opbouwen, en er dan voor zorgen dat jouw integratieroute die muur niet passeert. Hiernaast is als muur de positieve x-as gekozen. Zo'n route wordt wel een sleutelgatcontour genoemd.

Deze sleutelgatroute bestaat uit verschillende delen, die we apart zullen bekijken.

Van de grote cirkel gaat de straal naar oneindig, en omdat de functie f(z) = ^√z/_{(1 + z²)} sneller naar nul gaat dan ¹/_z zal die integraal naar nul gaan (zie de vorige les).

Op het kleine cirkeltje rond de oorsprong geldt z = reⁱ^φ Dan is dz = rieⁱ^φ dφ, en de integraal wordt:

Als f(z) een eindige functie is op dit cirkeltje, dan gaat dit ook naar nul als r naar nul gaat.

Er blijven twee stukken langs de reële as over. Een stuk net boven de as voor x van nul naar oneindig plus een stuk net onder de as voor x van oneindig naar nul. En die stukken zijn precies de integraal die we zoeken. Dat hebben we dan maar weer mooi voor elkaar!!!
Normaal vallen die twee routes (die immers oneindig dicht bij elkaar liggen) tegen elkaar weg, maar omdat ze in dit geval aan weerszijden van een vertakkingslijn liggen is dat niet meer zo! Die muur zit ertussen, en daarlangs maakt de functie een sprong.

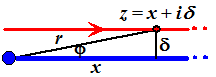
Hiernaast zie je zo'n punt z = x + iδ van de bovenste route.

Als δ naar nul gaat, dan wordt x ongeveer gelijk aan r, en dan is δ ongeveer gelijk aan rφ. dan kun je dat punt z schrijven als z = re^iφ ≈ xe^iδ/r ≈ x • eⁱ^δ/xDat kun je ook al wel zien aan de reeksontwikkeling van eⁱ^d^δ^x, want eⁱ^δ^/x = 1 + i^δ/_x + ¹/₂• (i^δ/_x)² + ¹/₆• (i^δ/_x)³ + .....
Als δ naar nul gaat wordt dat ongeveer gelijk aan 1 + i^δ/_x.
Dus dan is x • eⁱ^δ^/x = x (1 + i^δ/_x) = x + iδ

Maar voor die onderste tak is de hoek φ een afstand 2π verderop (je moet wel tegen de klok in draaien, want je mag niet in één keer naar -φ gaan omdat je dan die muur overgaat) dus dan is z = x • eⁱ^{(2π
-
δ/x)}
Tel nu beide integralen op:

(voor de noemer heb ik uit gemakzucht gewoon 1 + z² laten staan, want die is bij beide integralen gelijk; die functie heeft geen vertakkingslijn).
De teller van die laatste integrand gaat naar x^0,5 • (1 - e^{0,5 • 2πi}) want die stukken met e^±^iδ/x gaan naar 1 als ^δ/_x naar nul gaat. Dat geeft dan de volgende integraal voor beide rechte stukken samen:

Maar met de stelling van Cauchy kun je die eerste kringintegraal uitrekenen met de som van de residuen. De integrand heeft twee residuen: eentje bij z = i en eentje bij z = -i, want ^√z/_{(1 + z²)} = ^√z/_{(z
- i)(z + i)}
Het residu bij z = i geeft bijdrage 2πi • ^√i/_{(i
+ i)}= π√i = ¹/₂π√2 + ¹/₂πi√2
Het residu bij z = -i geeft bijdrage 2πi • ^√-i/_(-i_{- i)}= -π√(-i) = ¹/₂π√2 - ¹/₂πi√2 (voor √-i moet je weer weer vanaf de reële as halverwege naar naar -i draaien: denk aan die blauwe muur van hierboven).

Samen is dat π√2, en dat is 2 keer onze integraal, dus onze gezochte integraal is gelijk aan ¹/₂π√2

Een algemene formule.

In het voorbeeld hierboven deed die noemer er eigenlijk niet toe; pas bij het berekenen van de residuen werd die belangrijk. En verder kun je √x in dit voorbeeld net zo goed vervangen door een andere macht van x; het verhaal blijft exact gelijk!
Als je dat doet, dan vind je het volgende algemenere resultaat:

Wat zijn de voorwaarden?

Tijdens de berekeningen van dit voorbeeld zijn er een paar aannames gemaakt, die ik toch nog maar even herhaal:

De functie z^p • f(z) moet sneller naar nul gaan dan ¹/_z, want anders geeft de integraal over die grote cirkel niet nul.

De functie f(z) moet in de buurt van de oorsprong eindig blijven, want anders geeft de integraal van dat kleine cirkeltje niet nul.

De functie f(z) moet analytisch zijn in het complexe vlak (op een eindig aantal singulariteiten na) want anders mag je de residustelling van Cauchy niet gebruiken.