De binomiale verdeling.

© h.hofstede (h.hofstede@hogeland.nl)
Bij berekeningen met kansbomen zie je heel veel dezelfde `soort` problemen, met een duidelijke regelmaat.
Neem de volgende twee:
1. Met een viervlaksdobbelsteen hiernaast gooi je 12 keer.
Hoe groot is de kans op 5 keer het getal 3?

2. Van alle fietsers rijdt 15% door rood licht.
Hoe groot is dan de kans dat van de 10 fietsers er precies 3 door rood licht rijden?
De oplossingen zijn intussen makkelijk:
1. Eén gunstige tak is (D = 3, N = niet-3):   DDDDDNNNNNNN met kans  0,255 • 0,757
er zijn (12 nCr 5) zulke takken dus de kans is  (12 nCr 5) • 0,255 • 0,757 
2. Eén gunstige tak is (W = wel door rood, N = niet door rood):  WWWNNNNNNN met kans  0,153 • 0,857
Er zijn  (10 nCr 3) zulke takken dus de kans is  (10 nCr 3) • 0,153 • 0,857
Wat hebben deze problemen gemeenschappelijk?
Nou, bijna alles, wiskundig gezien.
Het gaat steeds om een aantal "experimenten"  (12 keer gooien, 10 fietsers)  waarbij er elke keer een "kans op succes" is  (0,25 bij de dobbelsteen, 0,15 bij de fietsers) en er wordt gevraagd naar  een bepaald aantal successen (5 drieën  en  3 fietsers door rood).
Deze drie getallen bepalen het hele probleem. Kijk maar naar de oplossingen:
(12 nCr 5) • 0,255 • 0,757 
(10 nCr 3) • 0,153 • 0,857

Vervang het aantal experimenten door de letter n,  de kans op succes per keer door de letter p,  en het gevraagde aantal successen door de letter k, dan staat hier:

(n  nCr k) • pk • (1 - p)n - k

Ga dat zelf maar na.
Daarbij zijn nog twee andere overeenkomsten:

•

 Het gaat steeds om experimenten "met terugleggen". Dat wil zeggen dat de kansen bij de takken van de kansboom gelijk blijven (steeds 0,25 en 0,75  of  0,15 en 0,85  of  p en (1-p))
•

Er zijn elke keer maar twee mogelijke uitkomsten, dus de boom splitst zich steeds in tweeën  (steeds  drie - niet drie  en  rood - niet rood  en  succes - niet succes)
Als aan deze twee voorwaarden is voldaan dan geldt het systeem van hierboven. Dat heet binomiaal en wordt dus zoals we al zagen gekenmerkt door drie getallen  (n, p, k).
Samengevat:
BINOMIAAL:
• met terugleggen.
• twee mogelijkheden per keer.
 
aantal experimenten n
kans op succes per keer  p
gevraagd k successen
P(k) = (n  nCr k) • pk • (1 - p)n - k
Waarom is dit handig om te weten?  Nou, omdat dit "systeem" nogal vaak voorkomt en omdat er zo'n handige kant en klare formule voor is, is er een knop op je rekenmachine gemaakt die dit allemaal in één keer voor je berekent.
Toets in 2nd - DISTR en kies optie 0:  binompdf
Daarachter zet je tussen haakjes  n, p, k  gescheiden door een dikke komma (die boven de 7)

Voor de viervlakdobbelsteen geeft dat  binompdf(12, 0.25, 5) = 0,1032
Voor de fietsers door rood geeft dat  binompdf(10, 0.15, 3) = 0,1298
   
  OPGAVEN
1. Van een tennisspeler is bekend dat 58% van zijn eerste services in is, en 80% van zijn tweede services.
     
a. Bereken de kans dat bij 30 servicebeurten 10 keer de eerste service in is.
   

0,0038
b. Bereken de kans dat hij in 50 servicebeurten precies 8 dubbele fouten slaat.
     

0,0334
2. Je moet een toets van 30 vierkeuze-vragen maken, maar je hebt helemaal niet geleerd dus moet elk antwoord volledig gokken. Hoe groot is dan de kans dat je precies 12 vragen goed beantwoordt?
     

0,029
3. Uit gegevens van het CBS (Centraal Bureau voor de Statistiek) blijkt dat de kans dat een 30-jarige in Nederland nog 65 jaar of ouder wordt is gelijk aan  0,782.
Hoe groot is dan de kans dat van de 40 dertigjarigen die we bekijken er precies 10 vóór hun 65ste zullen sterven?
     

0,1285
4. Een verstrooide professor heeft twee luciferdoosjes met elk 60 lucifers. Hij stopt er eentje in zijn linkerjaszak en eentje in zijn rechterjaszak. Elke keer als hij een lucifer nodig heeft om zijn pijp aan te steken pakt hij willekeurig uit een jaszak een doosje en haalt er een lucifer uit, en stopt het doosje weer terug.

Op een gegeven moment haalt hij een doosje uit zijn rechterjaszak en merkt dat er geen lucifers meer inzitten (hij moet het toen hij laatste lucifer pakte verstrooid weer teruggedaan hebben). Als hij daarna het andere doosje bekijkt blijkt dat daar nog 10 lucifers inzitten.

Hoe groot is vooraf de kans dat dit zou gebeuren?
     

0,0242
5. Als ik wil inloggen bij mijn provider op internet, dan lukt dat niet altijd.
Het blijkt dat het in 96% van de gevallen lukt, en dus in 4% niet.
     
a. Op een avond probeer ik in te loggen. Bereken de kans dat het pas de vijfde keer lukt.
   

0,00000246
b. Bereken de kans dat het van de 80 keer inloggen precies 72 keer lukt.
     

0,01
6. Je kent ze wel; die mensen die in winkelstraten zogenaamd gratis kranten staan uit te delen. Maar als je er eentje wilt aannemen blijkt dat je ook nog een enquête moet invullen. Het blijkt dat 85% van de winkelende mensen zo'n krant wel wil aannemen, maar dat daarvan slechts 12% bereid is de enquête in te vullen. 
     
a. Hoe groot is de kans dat er van de 80 winkelende mensen precies 60 een krant willen aannemen?
   

0,0068
b. Hoeveel winkelende mensen  zal een medewerker gemiddeld moeten aanspreken om 250 enquêtes te krijgen ingevuld?
   

2451
  c. Hoe groot is de kans dat van 30 winkelende mensen er 25 de krant willen aannemen waarvan er 3 willen meedoen aan de enquête?
   

0,0444
     
7. Om te kijken of een automobilist dronken is liet de politie hem of haar vroeger vaak over een rechte lijn lopen.
Een automobiliste is zó dronken dat zij telkens willekeurig een stap vooruit of achteruit neemt. 
De kans op beiden is 50%.
Neem voor het gemak aan dat zij wel op een rechte lijn blijft en dat alle stappen vreemd genoeg even groot zijn.

Hoe groot is de kans dat zij na 10 stappen weer op haar beginpunt staat?
     

0,2461
8. Net als ik deze opgave wil intoetsen stoot ik per ongeluk een bakje punaises om. Mopperend begin ik ze van de vloer te rapen. Maar dan valt me iets op:
Punaises kunnen op twee manieren op de grond vallen:
 
met de punt omhoog:       of met de punt omlaag:  
  Ik tel tijdens het oprapen hoeveel er op welke manier zijn gevallen, en dat levert me uiteindelijk op dat ik nu weet dat de kans dat een punaise met de punt omhoog komt te liggen 30% is, en met de punt naar beneden 70%.

Dat brengt me op een leuk idee:  ik ga een alternatieve dobbelsteen maken waar je 0 tm 8 mee kunt gooien.
Dat doe ik door acht punaises in een plastic doosje te doen en dat dicht te plakken. Als ik er dan mee rammel en het op tafel zet, kan ik tellen hoeveel punten er omhoog steken. Dat is het aantal "ogen" dat ik gegooid heb! Grappig niet? Een dobbelsteen waar je 0 t.m. 8 mee kunt gooien! En de kans op elk aantal is niet gelijk!

Hoe groot is de kans om met deze dobbelsteen een even aantal te gooien?
     

0,5003
       
9. examenvraagstuk  VWO, 1984.  
       
  Men speelt een spel met een pion in een speelveld dat voorzien is van een rechthoekig assenstelsel Oxy (zie figuur). Het spel bestaat uit een reeks zetten van de pion in het speelveld.
Elke zet van de pion wordt bepaald door de uitkomst van een worp met een zuivere dobbelsteen. Bij de uitkomst "één of twee ogen" wordt de pion vanuit zijn plaats in het speelveld één eenheid in de positieve x-richting verzet.
Bij de uitkomst "drie of meer ogen"  wordt de pion vanuit zijn plaats in het speelveld één eenheid in de positieve y-richting verzet.
Bij het begin van het spel staat de pion in (0,0)
Tijdens het spel beweegt de pion zich dus van roosterpunt naar roosterpunt.
     
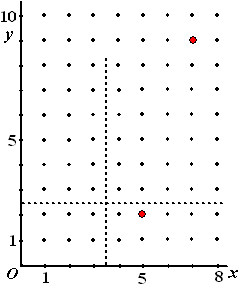  a. In welke roosterpunten kan de pion zich - vanuit de beginstand - na precies drie zetten bevinden?
Bereken bij elk van die punten de kans dat de pion dat punt bereikt.
       
  b. Bereken in vier decimalen nauwkeurig de kans dat de pion - vanuit de beginstand - via het punt (5,2) het punt (7,9) bereikt.
       

© h.hofstede (h.hofstede@hogeland.nl)